对数函数

(共34张PPT)
1
0
新课导入
回顾旧知
……
还记得得出表达式？
问题
在学习指数函数时，我们引用了细胞分裂的例子，得出分裂个数（y）与分裂次数（x）的函数关系：如下
根据对数定义，将x、y互解，可得到：
改写习惯形式（x→y，y → x），得：
指数函数
是函数吗？
推 广
指数函数一般式为：
将x、y互解，可得到：
是函数吗？什么函数？
改写习惯形式（x→y，y → x），得：
知识要点
对数函数定义：
一般地，我们把函数
(a>0,且a≠1)叫做对数函数，其中x是自变量 ，函数的定义域是
（1）为什么定义域为
（2）为什么规定底数ａ＞０且ａ≠１呢？
（3）函数的值域是什么？
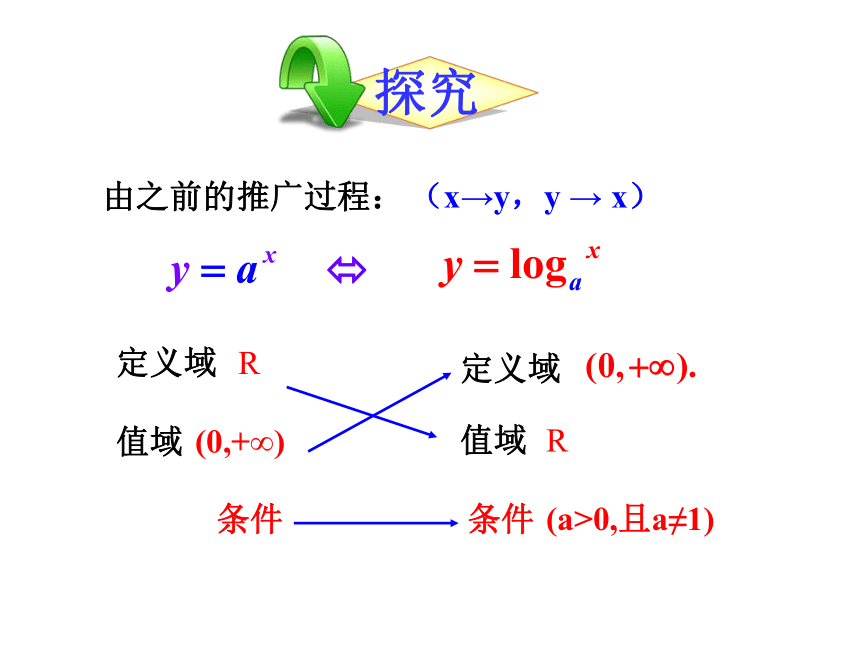
探究
由之前的推广过程：

定义域
值域
定义域
值域
条件
条件
R
(a>0,且a≠1)
（x→y，y → x）
R
(0,+∞)
小练习
求下列函数的定义域：
解：(1)因为x3>0,即x>0，所以(1)的定义域为{x|x>0};
(2)因为x2-1>0且x2-1≠0,即x>1或x<-1，所以(2)的定义域为{x|x>1或x<-1};
(3)因为9-x2>0,即-33，所以(3)的定义域为{x|-33}.
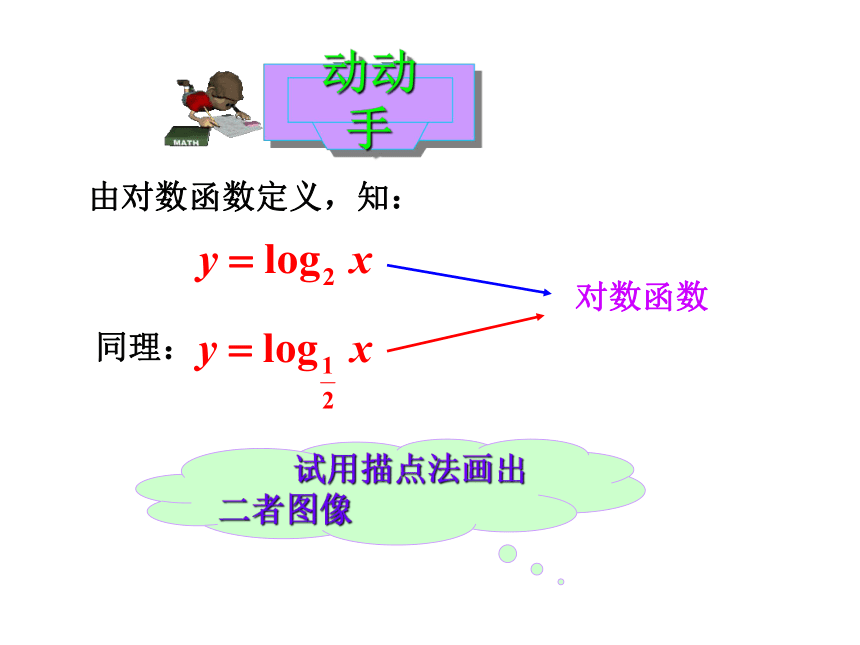
动动手
由对数函数定义，知：
对数函数
同理：
试用描点法画出二者图像
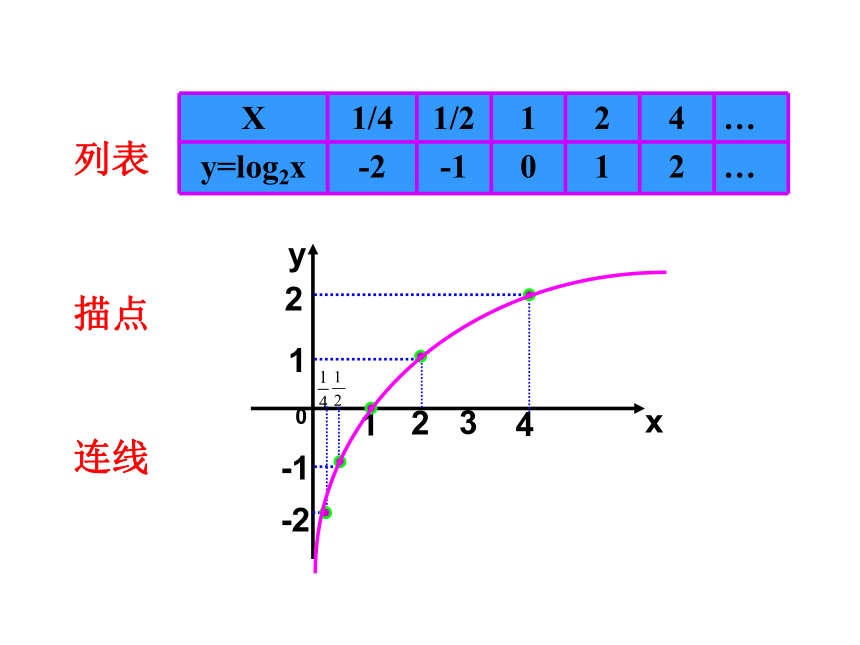
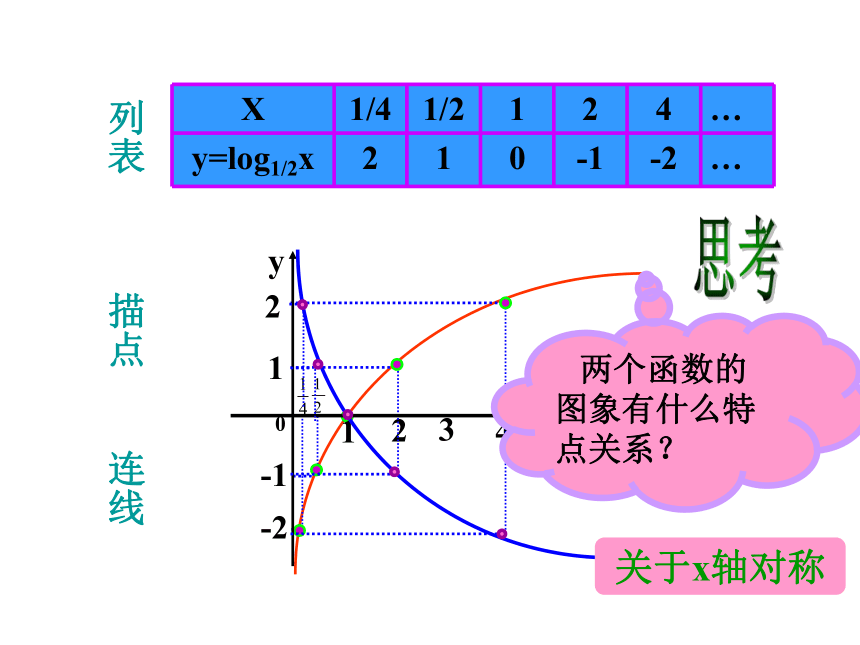
列表
X 1/4 1/2 1 2 4 …
y=log2x -2 -1 0 1 2 …
描点
2
1
-1
-2
1
2
4
0
y
x
3
连线
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
两个函数的图象有什么特点关系？
关于x轴对称
X 1/4 1/2 1 2 4 …
y=log1/2x 2 1 0 -1 -2 …
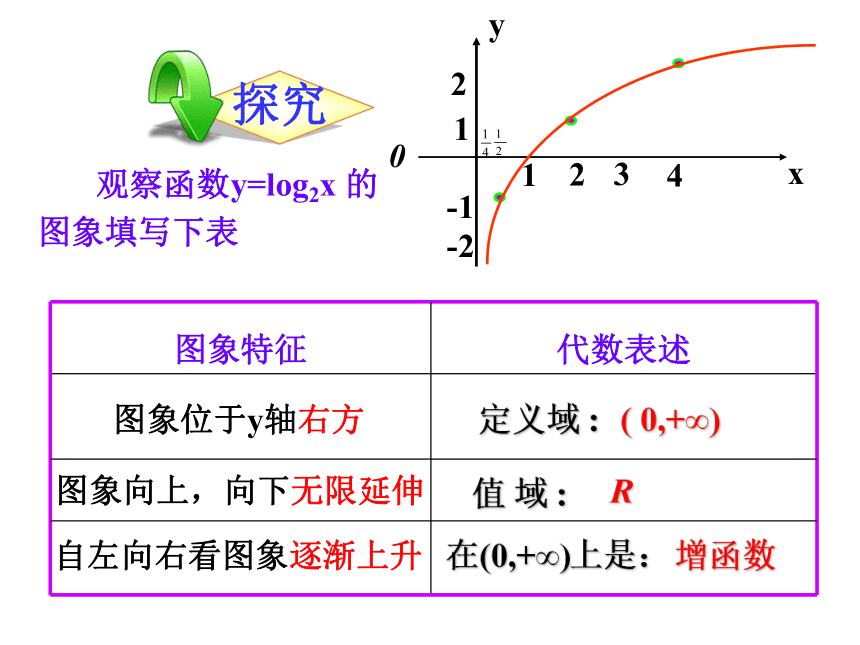
图象特征 代数表述
　 　
　 　
　
　
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是：
观察函数y=log2x 的图象填写下表
图象位于y轴右方
图象向上，向下无限延伸
自左向右看图象逐渐上升
2
1
-1
-2
1
2
4
0
y
x
3
探究
2
1
-1
-2
1
2
4
0
y
x
3
观察函数
的图象填写下表
图象特征 代数表述
　 　
　 　
　
　
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是：
图象位于y轴右方
图象向上，向下无限延伸
自左向右看图象逐渐下降
知识要点
对数函数图像和性质：
（见下表）
a>1
0图 象
性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过 点：
( 1, 0 )
x>1,y>0;
x<1, y<0
上增函数
x<1,y>0;
x>1, y<0
上减函数
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
( 0 , + ∞ )
( 0 , + ∞ )
小练习
比较下列各组数中两值的大小：
解：(1)令y=log2x，在（0，+∞）上是增函数，又因为2.5<3.1，所以log22.5< log23.1.
(2)令y=log0.3x，在（0，+∞）上是减函数，又因为2.5<3.1，所以log22.5> log23.1.
(3)当a>1,y=logax，在（0，+∞）上是增函数，又因为2.5<3.1，所以loga2.5< loga3.1.
当0 loga3.1.
探究总结
比较对数大小——常用方法，如下
1.观察底数是大于1还是小于1；
（ a>1时为增函数，02.比较真数值的大小；
3.根据单调性得出结果.
若底数不确定，那就要对底数进行分类讨论
即0 1
探究
用描点法作出函数
如下：
对比
2
1
-1
-2
1
2
4
0
y
x
3
底数变化时，图像变化趋势？
两两有何对称关系？
结论
当a>1,x轴上方图像自上向下，底数a越来越大.
当0函数y=logax与y=log(1/a)x关于x轴对称.
在问题提出时，我们将
的x、y互解，得到
（x→y，y → x）
习惯做法

有什么对应关系？
因为
得来，
是由
(y∈(0,+∞))是
(x∈R)的反函数.
（x→y，y → x）
习惯做法
(y∈(0,+∞))和
(x∈R)互为反函数.
这样，对于任一个y∈(0,+∞),通过式子,x在R 上都有唯一确定值和它对应，所以可以把x作为y的函数，我们就称：
知识要点
对数函数
互为反函数．
和
指数函数
(a>0,且a≠1)
课堂小结
1. 对数函数概念
函数y = logax(a 0，且a 1)叫做对数函数，其中x是自变量 .函数的定义域是(0,+∞) .
◆方法指导:
研究对数函数时，将a分为a>1和02.指数函数图像
（a>1）
（0y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
3.对数函数性质
（1）定义域： 值域：
（2）函数的特殊值：
（3）函数的单调性：
◆方法指导
利用函数图像研究函数性质是一种直观而形象的方法，记忆指数函数性质时可以联想它的图像.
4.比较对数大小——常用方法，如下
（1）观察底数是大于1还是小于1；
(若底数不确定，那就要对底数进行分类讨论)；
（2）比较真数值的大小；
（3）根据单调性得出结果.
底数不确定时，那就要对底数进行分类讨论
即0 1
5.指数函数与对数函数之间关系：
对数函数
互为反函数．
和
指数函数
(a>0,且a≠1)
说明：
与
图像关于y=x对称.
互为反函数的性质
随堂练习
1.求下列函数的定义域：
解：(1)因为(1-x)2>0,即x≠1，所以(1)的定义域为{x|x≠1 };
(2)因为1/(x3-1)>0且x3-1≠0,即x>1，所以(2)的定义域为{x|x>1 };
(3)因为 且x2>0,即x ≠0且x≠1或x≠-1 ，所以(3)的定义域为{x|x≠0且x≠1或x≠-1 };
(4)因为 且x>0,即x ≥ 1，所以(4)的定义域为{x|x≥1 }.
2.比较下列各组数中两值的大小：
解：(1)令 在（0，+∞）上是增函数，又因为2<5，所以lg2< lg5. (2)令 在（0，+∞）上是增函数，又因为2.5<3.9，所以ln2.5< ln3.9.
(3)因为 ，当a>1时，x轴上方图像自上向下，底数越来越大；所以x固定时，底数越大函数值反而越小，所以 .
(4)因为 ，当03.比较下列两组数中两值的大小：
借助0或1或中间数进行比较
(2)因为 ，当a>1时，x轴上方图像自上向下，底数越来越大；所以log351时候函数是递增的，所以log254. 当生物死后,它机体内原有的碳-14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳-14含量P 与死亡年数t之间的关系式：
问：经过多少年后生物体内碳-14含量P为原来的1/16
解：
由函数关系得：
代入p=1/16得：