沪教版(上海)高中数学高一下册 6.3 函数 y=Asin(ωx+φ) 的图像与性质(第一课时)教案
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 6.3 函数 y=Asin(ωx+φ) 的图像与性质(第一课时)教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 20:54:26 | ||
图片预览



文档简介
函数
y=Asin(ωx+φ)
的图像与性质(第一课时)
一、教学内容解析
1.教材地位
函数是描述周期现象的数学模型,也是一种基本初等函数,在本章中是重点内容,在数学和其他领域中具有具有十分重要的应用.本节课通过揭示参数、、对函数图像的影响,让学生有助于进一步深化对函数图像变换的理解,同时也有助于体会三角函数是描述周期现象的重要数学模型,是发展学生数学学科核心素养,培养学生的理性思维、创新意识和实践能力的重要载体.
2.教学任务
本节课主要通过“五点法”作图,探讨函数的图像与函数的图像之间的关系.图像是由点构成的,图像变换的实质是图像上点的变换,因此,欲研究函数图像的变换规律,只需研究图像上每个点的变化规律.
本节课教学设计是先分别探讨对函数、对函数的图像的变化规律,最后探究的图像和函数的图像之间的变化规律.其中,对的图像的变化规律的探讨方法可以迁移到后续问题解决中去.
3.教学重点
探讨、对函数、图像的变化规律.
二、教学目标设置
1.本节课借助flash动画和几何画板动态演示三角函数图像,探索并发现A对函数()图像及φ对函数图像的变化规律,让学生进一步了解三角函数图像各种变换的实质,并能够从中掌握函数图像变换的规律.
2.学生经历对函数、对函数图像变化规律的探究过程,培养学生数学发现能力和抽象概括能力;在研究各种变换的过程中,让学生体验由简单到复杂、由特殊到一般的化归思想,自始至终渗透了数形结合的思想.
3.通过三角函数图像变换规律的探求,培养学生的认知策略,发展元认识,培养学生的探索能力、钻研精神和科学态度,培养学生的数学核心素养.
三、学生学情分析
本节课课型为新授课,授课对象是高一学生,他们利用“五点法”画出正弦曲线、余弦曲线的图像,利用图像研究了他们的性质,掌握了三角函数周期性等相关知识,这为学生学习函数的图像与性质奠定了基础.
本节课的教学难点:(1)利用“五点法”画出函数和的简图;(2)函数的图像和函数的图像之间的关系.
四、教学策略分析
为了突破教学难点,呈现知识的发展过程,利用flash和几何画板软件辅助教学,充分发挥其直观和动态优势,可以对图像上每个点进行分析,引导学生逐步形成对函数图像的理解.该探讨方法可以迁移到其他函数的图像,有利于学生理解函数图像变换的数学本质.
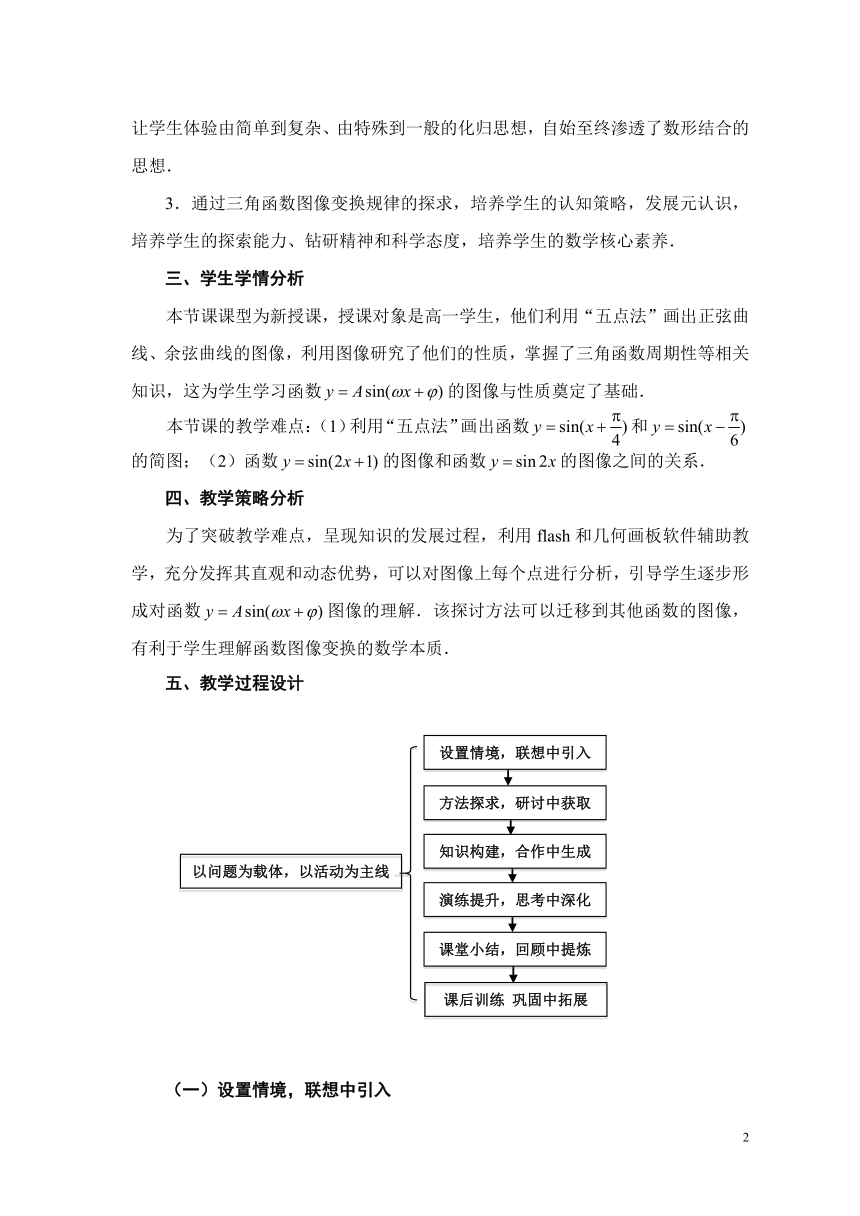
五、教学过程设计
(一)设置情境,联想中引入
借助摩天轮动画、简谐运动动画创设情境,引出刻画自然界周期现象的重要函数模型.
形如的函数在生活中经常可见,如弹簧振子在振动过程中离开平衡位置的位移满足,如图所示.再比如潮汐现象中水位的高度、单摆中的摆角等也满足这个解析式,因此今天我们来探讨这个函数,为了探讨方便,这里.
设计意图:1.通过生活中的摩天轮引出学生已经学习过的函数模型,唤起学生的回顾与思考,然后通过动画演示三个参数、、对函数的改变,这样从数学内部提出问题,并辅以丰富生动的现实背景,突出数学内部的发展规律,尽快让学生进入数学思考,相对于仅从现实生活背景突出问题,似乎更胜一筹;2.结合物理学中简谐振动生成函数创设问题情境,加强学科交叉联系,让学生体会到数学的应用价值.
(二)方法探求,研讨中获取
设问1:按照我们以往的经验,一般我们通过什么方法探讨函数的性质呢?
结论:函数的图像.
板书课题:函数的图像与性质
设问2:显然,参数、、取不同实数,我们就得到不同的函数,进而函数图像也会发生变化,在这个大家庭中,有你熟悉的函数吗?
结论:有,是函数.
设问3:如何研究三个参数、、对函数图像的影响呢?
结论:分而治之各个击破,然后再综合分析.
若先研究,令,;研究,令,;研究,令,.即分别研究函数、函数、函数的图像.
设计意图:1.面对一个新的数学问题,让学生去设计研究方案,重在引导学生思考解决问题的方法;2.通过概括和提炼,将学生的意识上升到“分而治之”的简单化思想层面,让学生明确“从特殊到一般”的探究方法,也为具体探究做好了铺垫.
(三)知识构建,合作中生成
1.探究参数对函数图像的影响.
通过设问,引导学生从特例入手,令,得正弦函数,令,得函数.然后画出它们的图像.
通过函数图像“五点法”作图入手,师生共同探究画出函数图像的方法,并通过观察它们的图像,发现两函数图像之间的关系:函数的图像可以看作是将的图像上每个点的横坐标不变,纵坐标伸长到原来的2倍而得到的.
再令,作出函数的图像.
通过观察三个函数图像,指导学生阅读教材,讨论三个函数性质的相同点与不同点,可以看出:在函数中,决定了函数的值域以及函数的最大值和最小值,通常称为振幅.得出结论:一般地,函数的图像,可以看作将函数的图像上每个点的横坐标保持不变,纵坐标伸长()或缩短()为原来的A倍而得到的.
设计意图:1.通过flash画板动态演示,较为直观地呈现参数A对图像的影响,学生能够比较容易得出感性认识,加深对振幅变换的理解;2.贯彻由特殊到一般、先猜想后验证的思想;3.以“五点法”作图为基础,注意在研究过程中提炼基本方法和程序,总结结论和规律,为学生后面的探究积累经验,提供示范.
2.探究参数对函数图像的影响.
引导学生继续从特例入手研究φ,φ分别取和,得到函数和和函数,并探究它们的函数图像.
在例2中,师生共同探究如何画出函数的图像,特别注意如何找出“五点法”中的关键点,再让学生合作探究画出函数的图像,并通过展台展示学生研究成果,学生分享研究心得.
实践操作
画出函数的简图.
解
(1)列表
(2)画图
教师利用几何画板在同一个直角坐标系中画出函数和的图像进行验证,从“形”的角度观察发现,把函数的图像向左平移个单位长度就可以得到函数的图像;把函数的图像向右平移个单位长度就可以得到的图像,指导学生通过函数图像
分析三个函数性质的相同点和不同点.通过例2的分析看出:在函数中,决定了时的函数值,通常称为初相,为相位.
最后,教师通过几何画板动态演示,得出结论:把函数图像向左(φ>0)或向右(φ<0)平移个单位长度,就可以得到函数的图像,即“左加右减”的平移规律.
设计意图:1.师生共同研究,观察猜想,作图验证,从“形”“数”两个角度分析,再由特殊到一般进行推广,从而得出结论;2.让学生充分体验探究发现的过程,掌握分析问题、解决问题的方法;3.通过独立思考、小组讨论、总结汇报,强化学生的学习体验和迁移能力,提升学生的合作意识和沟通能力.
(四)演练提升,思考中深化
1.基础训练
(1)为了得到函数的图像,只需将的图像上每个点(
)
A.横坐标伸长为原来的6倍,纵坐标不变
B.横坐标缩短为原来的倍,纵坐标不变
C.纵坐标伸长为原来的6倍,横坐标不变
D.纵坐标缩短为原来的倍,横坐标不变
答案:D
(2)将函数的图像上各点的纵坐标缩短为原来的倍(横坐标不变),所得到的图像的函数解析式为(
)
A.
B.
C.
D.
答案:B
(3)函数的图像如图所示,则的解析式可能是(
)
A.
B.
C.
D.
答案:D
设计意图:1.巩固学生对振幅、初相的理解;2.学会获取图像信息,巩固数形结合的数学思想;3.培养学生逆向思维能力,并为后面拓展训练中提出的问题奠定基础.
2.拓展训练
(1)如何由函数的图像得到函数的图像
(2)如何由函数的图像得到函数的图像
设计意图:1.学生通过合作互助,加深对平移问题本质的认识;2.教师借助“换元思想”提升问题的层次意识,实现突破难点.
3.课外探究
如何由函数的图像得到函数的图像
设计意图:1.回归到本节课开始的问题情景,指导学生课后思考如何由函数的图像得到函数的图像,最终实现函数的图像得到函数的图像,使之体验成功喜悦;2.为下一课时探讨对函数图像的影响拉开序幕,实现“为理解而学”的建构主义核心目标.
(五)课堂小结,回顾中提炼
1.与学生互动
本节课你有哪些认识与体会
2.与学生共同归纳
今点“明”言
三角图像颜值高,相位振幅变换巧;
都说五点作图好,缘于化归思想妙.
设计意图:通过小结对本节课的教学内容进行梳理和概括,在掌握知识的同时学会研究的方法,体会其中蕴含的数学思想.
(六)课后训练,巩固中拓展
1.阅读课本:第97~102页;
2.课后练习:课本第100页练习6.3(1)第1题(1),第102页练习6.3(2)第1题(1).
设计意图:巩固所学,拓展提升,各有所得.
六、板书设计
七、教学设计说明
本节课从生活实例入手得出函数,教师指导学生与函数的进行对比,发现它们的共同点与不同点,激发了学生的研究兴趣,这种在情境中进行联想顺应了学生的认知规律.与学生合作探究A、φ对函数图像的影响,并在此基础上,设计了两个拓展训练题,从一个参数对函数图像的影响升级为两个参数对函数图像的影响,步步深入,逐渐生成.知识构建的过程是根据学生已有经历,通过观察猜想,理性分析,得出结论.让学生在探究知识的同时,体会从特殊到一般,从简单到复杂的数学思想,从而掌握分析问题和解决问题的方法.
建构主义学习理论认为,知识不是通过教师传授获得的,而是学习者在一定的情境即社会文化背景下,利用必要的学习资料,通过意义建构的方式而获得的.本节课教学设计关注学生的学习兴趣,注重学生已有的学习经验,引导学生主动参与、乐于探究,鼓励学生用自己的语言进行表述,充分暴露学生的思维,鼓励学生对出现的不同结论进行探讨,找出问题的正确答案,有利于培养学生的学习积极性,有利于培养学生的思维能力,教师通过问题探究的形式,及时抓住学生的想法适时引导,有效驾驭课堂,把课堂还给学生共同完成问题探究.
设置情境,联想中引入
方法探求,研讨中获取
以问题为载体,以活动为主线
知识构建,合作中生成
演练提升,思考中深化
课堂小结,回顾中提炼
课后训练
巩固中拓展
PAGE
9
y=Asin(ωx+φ)
的图像与性质(第一课时)
一、教学内容解析
1.教材地位
函数是描述周期现象的数学模型,也是一种基本初等函数,在本章中是重点内容,在数学和其他领域中具有具有十分重要的应用.本节课通过揭示参数、、对函数图像的影响,让学生有助于进一步深化对函数图像变换的理解,同时也有助于体会三角函数是描述周期现象的重要数学模型,是发展学生数学学科核心素养,培养学生的理性思维、创新意识和实践能力的重要载体.
2.教学任务
本节课主要通过“五点法”作图,探讨函数的图像与函数的图像之间的关系.图像是由点构成的,图像变换的实质是图像上点的变换,因此,欲研究函数图像的变换规律,只需研究图像上每个点的变化规律.
本节课教学设计是先分别探讨对函数、对函数的图像的变化规律,最后探究的图像和函数的图像之间的变化规律.其中,对的图像的变化规律的探讨方法可以迁移到后续问题解决中去.
3.教学重点
探讨、对函数、图像的变化规律.
二、教学目标设置
1.本节课借助flash动画和几何画板动态演示三角函数图像,探索并发现A对函数()图像及φ对函数图像的变化规律,让学生进一步了解三角函数图像各种变换的实质,并能够从中掌握函数图像变换的规律.
2.学生经历对函数、对函数图像变化规律的探究过程,培养学生数学发现能力和抽象概括能力;在研究各种变换的过程中,让学生体验由简单到复杂、由特殊到一般的化归思想,自始至终渗透了数形结合的思想.
3.通过三角函数图像变换规律的探求,培养学生的认知策略,发展元认识,培养学生的探索能力、钻研精神和科学态度,培养学生的数学核心素养.
三、学生学情分析
本节课课型为新授课,授课对象是高一学生,他们利用“五点法”画出正弦曲线、余弦曲线的图像,利用图像研究了他们的性质,掌握了三角函数周期性等相关知识,这为学生学习函数的图像与性质奠定了基础.
本节课的教学难点:(1)利用“五点法”画出函数和的简图;(2)函数的图像和函数的图像之间的关系.
四、教学策略分析
为了突破教学难点,呈现知识的发展过程,利用flash和几何画板软件辅助教学,充分发挥其直观和动态优势,可以对图像上每个点进行分析,引导学生逐步形成对函数图像的理解.该探讨方法可以迁移到其他函数的图像,有利于学生理解函数图像变换的数学本质.
五、教学过程设计
(一)设置情境,联想中引入
借助摩天轮动画、简谐运动动画创设情境,引出刻画自然界周期现象的重要函数模型.
形如的函数在生活中经常可见,如弹簧振子在振动过程中离开平衡位置的位移满足,如图所示.再比如潮汐现象中水位的高度、单摆中的摆角等也满足这个解析式,因此今天我们来探讨这个函数,为了探讨方便,这里.
设计意图:1.通过生活中的摩天轮引出学生已经学习过的函数模型,唤起学生的回顾与思考,然后通过动画演示三个参数、、对函数的改变,这样从数学内部提出问题,并辅以丰富生动的现实背景,突出数学内部的发展规律,尽快让学生进入数学思考,相对于仅从现实生活背景突出问题,似乎更胜一筹;2.结合物理学中简谐振动生成函数创设问题情境,加强学科交叉联系,让学生体会到数学的应用价值.
(二)方法探求,研讨中获取
设问1:按照我们以往的经验,一般我们通过什么方法探讨函数的性质呢?
结论:函数的图像.
板书课题:函数的图像与性质
设问2:显然,参数、、取不同实数,我们就得到不同的函数,进而函数图像也会发生变化,在这个大家庭中,有你熟悉的函数吗?
结论:有,是函数.
设问3:如何研究三个参数、、对函数图像的影响呢?
结论:分而治之各个击破,然后再综合分析.
若先研究,令,;研究,令,;研究,令,.即分别研究函数、函数、函数的图像.
设计意图:1.面对一个新的数学问题,让学生去设计研究方案,重在引导学生思考解决问题的方法;2.通过概括和提炼,将学生的意识上升到“分而治之”的简单化思想层面,让学生明确“从特殊到一般”的探究方法,也为具体探究做好了铺垫.
(三)知识构建,合作中生成
1.探究参数对函数图像的影响.
通过设问,引导学生从特例入手,令,得正弦函数,令,得函数.然后画出它们的图像.
通过函数图像“五点法”作图入手,师生共同探究画出函数图像的方法,并通过观察它们的图像,发现两函数图像之间的关系:函数的图像可以看作是将的图像上每个点的横坐标不变,纵坐标伸长到原来的2倍而得到的.
再令,作出函数的图像.
通过观察三个函数图像,指导学生阅读教材,讨论三个函数性质的相同点与不同点,可以看出:在函数中,决定了函数的值域以及函数的最大值和最小值,通常称为振幅.得出结论:一般地,函数的图像,可以看作将函数的图像上每个点的横坐标保持不变,纵坐标伸长()或缩短()为原来的A倍而得到的.
设计意图:1.通过flash画板动态演示,较为直观地呈现参数A对图像的影响,学生能够比较容易得出感性认识,加深对振幅变换的理解;2.贯彻由特殊到一般、先猜想后验证的思想;3.以“五点法”作图为基础,注意在研究过程中提炼基本方法和程序,总结结论和规律,为学生后面的探究积累经验,提供示范.
2.探究参数对函数图像的影响.
引导学生继续从特例入手研究φ,φ分别取和,得到函数和和函数,并探究它们的函数图像.
在例2中,师生共同探究如何画出函数的图像,特别注意如何找出“五点法”中的关键点,再让学生合作探究画出函数的图像,并通过展台展示学生研究成果,学生分享研究心得.
实践操作
画出函数的简图.
解
(1)列表
(2)画图
教师利用几何画板在同一个直角坐标系中画出函数和的图像进行验证,从“形”的角度观察发现,把函数的图像向左平移个单位长度就可以得到函数的图像;把函数的图像向右平移个单位长度就可以得到的图像,指导学生通过函数图像
分析三个函数性质的相同点和不同点.通过例2的分析看出:在函数中,决定了时的函数值,通常称为初相,为相位.
最后,教师通过几何画板动态演示,得出结论:把函数图像向左(φ>0)或向右(φ<0)平移个单位长度,就可以得到函数的图像,即“左加右减”的平移规律.
设计意图:1.师生共同研究,观察猜想,作图验证,从“形”“数”两个角度分析,再由特殊到一般进行推广,从而得出结论;2.让学生充分体验探究发现的过程,掌握分析问题、解决问题的方法;3.通过独立思考、小组讨论、总结汇报,强化学生的学习体验和迁移能力,提升学生的合作意识和沟通能力.
(四)演练提升,思考中深化
1.基础训练
(1)为了得到函数的图像,只需将的图像上每个点(
)
A.横坐标伸长为原来的6倍,纵坐标不变
B.横坐标缩短为原来的倍,纵坐标不变
C.纵坐标伸长为原来的6倍,横坐标不变
D.纵坐标缩短为原来的倍,横坐标不变
答案:D
(2)将函数的图像上各点的纵坐标缩短为原来的倍(横坐标不变),所得到的图像的函数解析式为(
)
A.
B.
C.
D.
答案:B
(3)函数的图像如图所示,则的解析式可能是(
)
A.
B.
C.
D.
答案:D
设计意图:1.巩固学生对振幅、初相的理解;2.学会获取图像信息,巩固数形结合的数学思想;3.培养学生逆向思维能力,并为后面拓展训练中提出的问题奠定基础.
2.拓展训练
(1)如何由函数的图像得到函数的图像
(2)如何由函数的图像得到函数的图像
设计意图:1.学生通过合作互助,加深对平移问题本质的认识;2.教师借助“换元思想”提升问题的层次意识,实现突破难点.
3.课外探究
如何由函数的图像得到函数的图像
设计意图:1.回归到本节课开始的问题情景,指导学生课后思考如何由函数的图像得到函数的图像,最终实现函数的图像得到函数的图像,使之体验成功喜悦;2.为下一课时探讨对函数图像的影响拉开序幕,实现“为理解而学”的建构主义核心目标.
(五)课堂小结,回顾中提炼
1.与学生互动
本节课你有哪些认识与体会
2.与学生共同归纳
今点“明”言
三角图像颜值高,相位振幅变换巧;
都说五点作图好,缘于化归思想妙.
设计意图:通过小结对本节课的教学内容进行梳理和概括,在掌握知识的同时学会研究的方法,体会其中蕴含的数学思想.
(六)课后训练,巩固中拓展
1.阅读课本:第97~102页;
2.课后练习:课本第100页练习6.3(1)第1题(1),第102页练习6.3(2)第1题(1).
设计意图:巩固所学,拓展提升,各有所得.
六、板书设计
七、教学设计说明
本节课从生活实例入手得出函数,教师指导学生与函数的进行对比,发现它们的共同点与不同点,激发了学生的研究兴趣,这种在情境中进行联想顺应了学生的认知规律.与学生合作探究A、φ对函数图像的影响,并在此基础上,设计了两个拓展训练题,从一个参数对函数图像的影响升级为两个参数对函数图像的影响,步步深入,逐渐生成.知识构建的过程是根据学生已有经历,通过观察猜想,理性分析,得出结论.让学生在探究知识的同时,体会从特殊到一般,从简单到复杂的数学思想,从而掌握分析问题和解决问题的方法.
建构主义学习理论认为,知识不是通过教师传授获得的,而是学习者在一定的情境即社会文化背景下,利用必要的学习资料,通过意义建构的方式而获得的.本节课教学设计关注学生的学习兴趣,注重学生已有的学习经验,引导学生主动参与、乐于探究,鼓励学生用自己的语言进行表述,充分暴露学生的思维,鼓励学生对出现的不同结论进行探讨,找出问题的正确答案,有利于培养学生的学习积极性,有利于培养学生的思维能力,教师通过问题探究的形式,及时抓住学生的想法适时引导,有效驾驭课堂,把课堂还给学生共同完成问题探究.
设置情境,联想中引入
方法探求,研讨中获取
以问题为载体,以活动为主线
知识构建,合作中生成
演练提升,思考中深化
课堂小结,回顾中提炼
课后训练
巩固中拓展
PAGE
9
