第三章 阶段培优练习题(练习范围3.1-3.3 字母表示数 代数式 代数式的值)2021-2022学年苏科版七年级数学上册(word版含答案)
文档属性
| 名称 | 第三章 阶段培优练习题(练习范围3.1-3.3 字母表示数 代数式 代数式的值)2021-2022学年苏科版七年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 10:02:38 | ||
图片预览




文档简介
第三章
阶段培优练习题(练习范围3.1-3.3字母表示数
代数式
代数式的值)
2021-2022学年苏科版七年级数学上册
一、选择题
1、用代数式表示:y与x的和的(
)
A.
B.
C.
D.
2、下列说法正确的是( )
A.多项式x2+2x2y+1是二次三项式
B.单项式2x2y的次数是2
C.0是单项式
D.单项式﹣3πx2y的系数是﹣3
3、下列说法中正确的个数是( )
(1)a和0都是单项式;
(2)多项式﹣3a2b+7a2b2﹣2ab+1是三次四项式;
(3)单项式的系数为﹣9;
(4)多项式x2+2xy﹣y2的项为x2、2xy、﹣y2.
A.1个
B.2个
C.3个
D.4个
4、下列说法中,正确的是( )
A.当x=2时,代数式x2+1的值是5
B.当a=3时,代数式a2﹣的值是12
C.当a=0时,代数式+1的值是1
D.代数式a2+b2的值恒为整数
5、若x﹣3y=﹣2,那么3﹣x+3y的值是( )
A.1
B.2
C.5
D.6
6、按图示的程序计算,若开始输入的x为正整数,最后输出的结果为67.则x的值可能是( )
A.3
B.7
C.12
D.23
7、当时,的值为18,则的值为(
)
A.40
B.42
C.46
D.56
8、把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形,,按此规律排列下去,则第⑧个图案中黑色三角形的个数为
A.10
B.18
C.21
D.36
9、下列各选项中,所列代数式错误的是(
).
A.表示“比a与b的积的2倍小5的数”的代数式是;
B.表示“a与b的平方差的相反数”的代数式;
C.表示“被5除商是a,余数是2的数”的代数式是;
D.表示“数a的一半与数b的3倍的差”的代数式是.
10、一个工程,甲独做要x小时,乙独做要y小时,两人合作3小时的工作量为(
)
A.3(x+y)
B.3()
C.
D.
二、填空题
11、下列代数式中①2 4,②,③x÷y,④x﹣2,其中书写正确的是_____.
12、如图,在一个长为b米,宽为a米的长方形草坪中间,有两条宽度都是c米的小径,则草地的总面积可表示为__________平方米.
13、(1)是五次单项式,则m= ;(2)若x2ym+1z2是五次单项式,则m= ;
(3)若xmyn+1z3是五次单项式,则2m+2n= ;(4)如果﹣5xym﹣2为四次单项式,则m= .
14、单项式的系数是 ,多项式2ab﹣3a2b2+1的次数是 .
15、已知,则代数式的值为________.
16、已知,,那么整式的值为_________.
17、a与b互为相反数,c与d互为倒数,m的绝对值为2,
则的值为_________.
18、如图所示是计算机程序计算,若开始输入,则最后输出的结果是 .
三、解答题
19、今年假期某校对操场进行了维修改造,如图是操场的一角.在长为a米,宽为b米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为c米.
(1)直接写出一个篮球场的长和宽;(用含字母a,b,c的代数式表示)
(2)用含字母a,b,c的代数式表示这两个篮球场占地面积的和,并求出当a=42,b=36,c=4时,这两个篮球场占地面积的和.
20、已知多项式(m﹣3)x|m|﹣2y3+x2y﹣2xy2是关于、y的四次三项式.
(1)求m的值;
(2)当x=,y=﹣1时,求此多项式的值.
21、观察下列单项式:﹣x,3x2,﹣5x3,7x4,…,﹣37x19,39x20,….
(1)这组单项式的系数的符号规律是
,系数的绝对值规律是
;
(2)这组单项式的次数的规律是
;
(3)根据上面的归纳,可以猜想第n个单项式是(只能填写一个代数式)
;
(4)请你根据猜想,写出第2008个、第2009个单项式,它们分别是
,
.
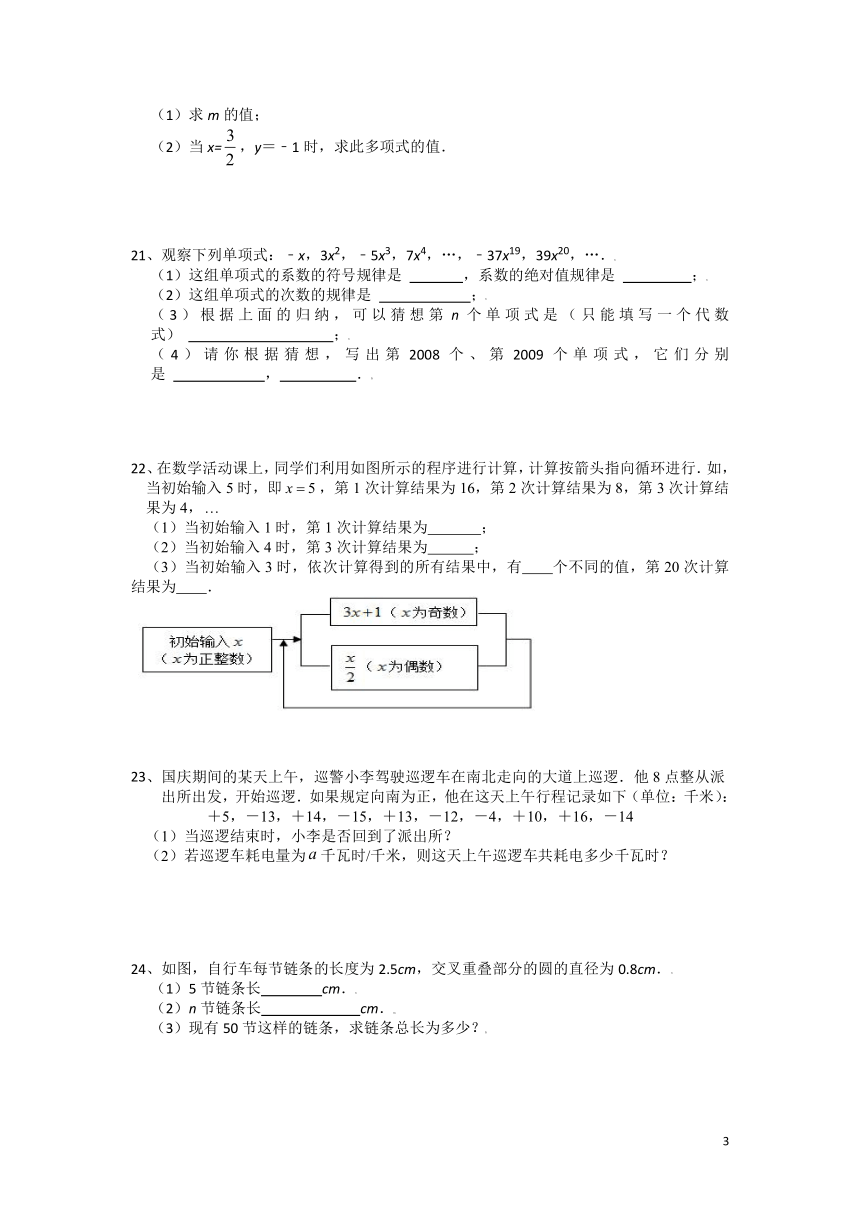
22、在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.如,当初始输入5时,即,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,
(1)当初始输入1时,第1次计算结果为
;
(2)当初始输入4时,第3次计算结果为
;
(3)当初始输入3时,依次计算得到的所有结果中,有 个不同的值,第20次计算结果为 .
23、国庆期间的某天上午,巡警小李驾驶巡逻车在南北走向的大道上巡逻.他8点整从派出所出发,开始巡逻.如果规定向南为正,他在这天上午行程记录如下(单位:千米):
+5,-13,+14,-15,+13,-12,-4,+10,+16,-14
(1)当巡逻结束时,小李是否回到了派出所?
(2)若巡逻车耗电量为千瓦时/千米,则这天上午巡逻车共耗电多少千瓦时?
24、如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)5节链条长
cm.
(2)n节链条长
cm.
(3)现有50节这样的链条,求链条总长为多少?
25、求代数式的值.
(1)已知:
,求的值;
(2)当时,求的值;
(3)已知:,求的值;
(4)与互为相反数,求代数式的值.
第三章
阶段培优练习题(练习范围3.1-3.3字母表示数
代数式
代数式的值)
2021-2022学年苏科版七年级数学上册(解析)
一、选择题
1、用代数式表示:y与x的和的(
)
A.
B.
C.
D.
【答案】A
【分析】y与x的和的,即为x与y先求和,然后再与相乘,据此列式即可.
【详解】解:y与x的和的,用代数式表示为.
故选:A.
2、下列说法正确的是( )
A.多项式x2+2x2y+1是二次三项式
B.单项式2x2y的次数是2
C.0是单项式
D.单项式﹣3πx2y的系数是﹣3
【分析】根据多项式、单项式、系数、常数项的定义分别进行判断,即可求出答案.
【解析】A.多项式x2+2x2y+1是三次三项式,此选项错误;
B.单项式2x2y的次数是3,此选项错误;
C.0是单项式,此选项正确;
D.单项式﹣3πx2y的系数是﹣3π,此选项错误;
故选:C.
3、下列说法中正确的个数是( )
(1)a和0都是单项式;
(2)多项式﹣3a2b+7a2b2﹣2ab+1是三次四项式;
(3)单项式的系数为﹣9;
(4)多项式x2+2xy﹣y2的项为x2、2xy、﹣y2.
A.1个
B.2个
C.3个
D.4个
【分析】根据单项式和多项式的相关定义解答即可.
【解析】(1)a和0都是单项式,原说法正确;
(2)多项式﹣3a2b+7a2b2﹣2ab+1是四次四项式,原说法错误;
(3)单项式的系数为,原说法错误;
(4)多项式x2+2xy﹣y2的项为x2、2xy、﹣y2,原说法正确.
说法中正确的个数是2个,
故选:B.
4、下列说法中,正确的是( )
A.当x=2时,代数式x2+1的值是5
B.当a=3时,代数式a2﹣的值是12
C.当a=0时,代数式+1的值是1
D.代数式a2+b2的值恒为整数
【分析】把字母的值代入代数式即可得到结论.
解:A、当x=2时,代数式x2+1的值是5,故正确;
B、当a=3时,代数式a2-
的值是5,故错误;
C、当a=0时,代数式
+1无意义,故错误;
D、代数式a2+b2的值恒为正数,故错误;
故选A.
5、若x﹣3y=﹣2,那么3﹣x+3y的值是( )
A.1
B.2
C.5
D.6
【分析】把x﹣3y=﹣2整体代入所求代数式求值即可.
【解析】当x﹣3y=﹣2时,原式=3﹣(x﹣3y)=3﹣(﹣2)=5.
故选:C.
6、按图示的程序计算,若开始输入的x为正整数,最后输出的结果为67.则x的值可能是( )
A.3
B.7
C.12
D.23
【分析】根据运算程序列出方程求得相应的x值,直到x不是正整数为止,然后对比选项即可得出答案.
【解析】∵最后输出的结果为67,∴3x+1=67,解得:x=22;
当3x+1=22时,解得:x=7;
当3x+1=7时,解得:x=2;
当3x+1=2时,解得:x=,
∵开始输入的x为正整数,
∴x=不合题意.
∴x的值可能为:2或7或22,
故选:B.
7、当时,的值为18,则的值为(
)
A.40
B.42
C.46
D.56
【答案】B
【分析】把代入计算结果18,变形后得,整体代入计算即可.
【解析】当时,,所以,所以,
则,
故选:B.
8、把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形,,按此规律排列下去,则第⑧个图案中黑色三角形的个数为
A.10
B.18
C.21
D.36
【分析】第①个图案中有1个黑色三角形,第②个图案中有个黑色三角形,第③个图案中有个黑色三角形,,按此规律排列下去,则第⑥个图案中黑色三角形的个数为个,结论可求.
【解答】解:第①个图案中有1个黑色三角形,
第②个图案中有个黑色三角形,
第③个图案中有个黑色三角形,
,
按此规律排列下去,则第⑧个图案中黑色三角形的个数为(个.
故选:.
9、下列各选项中,所列代数式错误的是(
).
A.表示“比a与b的积的2倍小5的数”的代数式是;
B.表示“a与b的平方差的相反数”的代数式;
C.表示“被5除商是a,余数是2的数”的代数式是;
D.表示“数a的一半与数b的3倍的差”的代数式是.
【答案】C
【分析】根据描述列出代数式进行判断即可.
【解析】
解:A、表示“比a与b的积的2倍小5的数”的代数式是,故此选项不符合题意;
B、表示“a与b的平方差的相反数”的代数式,故此选项不符合题意;
C、表示“被5除商是a,余数是2的数”的代数式是,故此选项符合题意;
D、表示“数a的一半与数b的3倍的差”的代数式是,故此选项不符合题意.
故选C.
10、一个工程,甲独做要x小时,乙独做要y小时,两人合作3小时的工作量为(
)
A.3(x+y)
B.3()
C.
D.
【答案】B
【解析】
【分析】根据甲、乙单独完成工作的时间,可以得到工作的效率,即可求解.
【解析】解:∵甲独做要x小时,乙独做要y小时
∴甲乙的工作效率分别为,所以合作三小时为3().
故选B.
二、填空题
11、下列代数式中①2 4,②,③x÷y,④x﹣2,其中书写正确的是_____.
【答案】④.
【解析】①2 4应为2×4;②x2应为x;③x÷y应为;④x-2书写正确,
综上所述,书写正确的是④.
12、如图,在一个长为b米,宽为a米的长方形草坪中间,有两条宽度都是c米的小径,则草地的总面积可表示为__________平方米.
【答案】
【分析】分别求出小径的面积和长方形的面积,再得出答案即可.
【详解】解:草地的总面积可表示为平方米,
故答案为:平方米.
13、(1)是五次单项式,则m= ;(2)若x2ym+1z2是五次单项式,则m= ;
(3)若xmyn+1z3是五次单项式,则2m+2n= ;(4)如果﹣5xym﹣2为四次单项式,则m= .
【分析】(1)直接利用单项式的次数确定方法分别分析得出答案;
(2)直接利用单项式的次数确定方法分别分析得出答案;
(3)直接利用单项式的次数确定方法分别分析得出答案;
(4)直接利用单项式的次数确定方法分别分析得出答案.
【解析】(1)∵是五次单项式,
∴2+m﹣1=5,
解得:m=4.故答案为:4;
(2)若x2ym+1z2是五次单项式,则2+m+1+2=5,
解得:m=0;故答案为:0;
(3)若xmyn+1z3是五次单项式,则m+n+1+3=5,
则m+n=1,
故2m+2n=2;故答案为:2;
(4)如果﹣5xym﹣2为四次单项式,则1+m﹣2=4,
解得:m=5.故答案为:5.
14、单项式的系数是 ,多项式2ab﹣3a2b2+1的次数是 .
【分析】利用单项式系数定义以及多项式的次数进行解答即可.
【解析】∵单项式中的数字因数叫做单项式的系数.
∴单项式系数是,
∵多项式中次数最高项的次数叫做多项式的次数.
∴多项式2ab﹣3a2b2+1的次数是4.
故答案为:,4.
15、已知,则代数式的值为________.
【答案】9
【分析】把所求代数式整理成已知条件的形式,然后代入进行计算即可求解.
【解析】解:∵,
∴
.
故答案为:
.
16、已知,,那么整式的值为_________.
【答案】14
【分析】先对代数式进行变形,然后利用整体代入进行求解即可.
【解析】
把作为整体代入,.
故答案为14
17、a与b互为相反数,c与d互为倒数,m的绝对值为2,
则的值为_________.
【答案】-11
【分析】根据a与b互为相反数,c与d互为倒数,m的绝对值为2,可得,,,将化简可得,根据当时,当时,分别求值即可.
【解析】解:∵a与b互为相反数,c与d互为倒数,m的绝对值为2,
∴,,,
∵
当时,,
当时,,
故答案是:-11.
18、如图所示是计算机程序计算,若开始输入,则最后输出的结果是 .
【分析】把的值代入程序中计算即可求出所求.
【解答】解:把代入程序得:,
把代入程序得:,
则最后输出的结果为.
故答案为:.
三、解答题
19、今年假期某校对操场进行了维修改造,如图是操场的一角.在长为a米,宽为b米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为c米.
(1)直接写出一个篮球场的长和宽;(用含字母a,b,c的代数式表示)
(2)用含字母a,b,c的代数式表示这两个篮球场占地面积的和,并求出当a=42,b=36,c=4时,这两个篮球场占地面积的和.
【解题思路】(1)根据题意求出两个长方形的长和宽,即可;
(2)把a=42,b=36,c=4代入(b﹣2c)(a﹣3c)求出即可.
【解答过程】(1)一个篮球场的长和宽分别为:(b﹣2c),(a﹣3c);
(2)这两个篮球场的占地面积为(b﹣2c)(a﹣3c)(平方米);
当a=42,b=36,c=4时,(42﹣4×3)×(36﹣2×4)=840(平方米).
20、已知多项式(m﹣3)x|m|﹣2y3+x2y﹣2xy2是关于、y的四次三项式.
(1)求m的值;
(2)当x=,y=﹣1时,求此多项式的值.
【分析】(1)直接利用多项式的次数的确定方法得出m的值;
(2)将x,y的值代入求出答案.
【解析】(1)∵多项式(m﹣3)x|m|﹣2y3+x2y﹣2xy2是关于xy的四次三项式,
∴|m|﹣2+3=4,m﹣3≠0,
解得:m=﹣3,
(2)当x=,y=﹣1时,此多项式的值为:
21、观察下列单项式:﹣x,3x2,﹣5x3,7x4,…,﹣37x19,39x20,….
(1)这组单项式的系数的符号规律是
,系数的绝对值规律是
;
(2)这组单项式的次数的规律是
;
(3)根据上面的归纳,可以猜想第n个单项式是(只能填写一个代数式)
;
(4)请你根据猜想,写出第2008个、第2009个单项式,它们分别是
,
.
【分析】所有式子均为单项式,先观察数字因数,可得规律:(﹣1)n(2n﹣1),再观察字母因数,可得规律:xn,然后代入求值即可.
【解析】(1)单项式的系数依次为:﹣1,3,﹣5,7,﹣9,11, ,为奇数且奇次项为负数,
可得规律:(﹣1)n(2n﹣1),
故答案为:(﹣1)n(或:负号正号依次出现),(2n﹣1);
(2)观察易知次数的规律为从1开始的连续自然数,
故答案为:从1开始的连续自然数;
(3)结合(1)和(2)可得第n个单项式为:(﹣1)n(2n﹣1)xn,
故答案为:(﹣1)n(2n﹣1)xn;
(4)把n=2008、n=2009直接代入(﹣1)n(2n﹣1)xn中,即可分别得到:4015x2008,﹣4017x2009,
故答案为:4015x2008,﹣4017x2009.
22、在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.如,当初始输入5时,即,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,
(1)当初始输入1时,第1次计算结果为
;
(2)当初始输入4时,第3次计算结果为
;
(3)当初始输入3时,依次计算得到的所有结果中,有 个不同的值,第20次计算结果为 .
【分析】(1)把代入指定的关系式求值即可;
(2)把代入指定的关系式计算第1次的结果,再根据结果的奇偶数,进行第2次运算,依此类推,求出第3次计算结果即可;
(3)把代入指定的关系式计算第1次的结果,再根据结果的奇偶数,进行第2次运算依此类推,发现其计算结果有规律,按照规律,求出第20次计算结果即可;
【解答】解:(1)当时,,故答案为:4;
(2)当时,第1次结果为:,第2次结果为,第3次结果为;
故答案为:4;
(3)当时,
第1次结果为:,
第2次结果为,
第3次结果为;
第4次结果为,
第5次结果为,
第6次结果为,
第7次结果为,
第8次结果为,
,第20次运算的结果为4.
有7个不同的值,
故答案为:7,4.
23、国庆期间的某天上午,巡警小李驾驶巡逻车在南北走向的大道上巡逻.他8点整从派出所出发,开始巡逻.如果规定向南为正,他在这天上午行程记录如下(单位:千米):
+5,-13,+14,-15,+13,-12,-4,+10,+16,-14
(1)当巡逻结束时,小李是否回到了派出所?
(2)若巡逻车耗电量为千瓦时/千米,则这天上午巡逻车共耗电多少千瓦时?
【答案】(1)回到了派出所;(2)千瓦时
【分析】(1)将所有数相加再对比即可得出答案;
(2)先将所有数的绝对值相加,再乘即可得出答案.
【详解】
解:(1)(千米).
答:小李回到了派出所.
(2)
(千米),
(千瓦时)
答:这天上午巡逻车共耗油千瓦时.
24、如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)5节链条长
cm.
(2)n节链条长
cm.
(3)现有50节这样的链条,求链条总长为多少?
【分析】(1)根据图形找出规律计算5节链条的长度即可;
(2)由(1)写出表示链条节数的一般式;
(3)根据(2)计算即可求解.
【解析】(1)根据图形可得出:
2节链条的长度为:2.5×2﹣0.8(cm),
3节链条的长度为:2.5×3﹣0.8×2(cm),
4节链条的长度为:2.5×4﹣0.8×3(cm),
5节链条的长度为:2.5×5﹣0.8×4=9.3(cm).
故答案为:9.3cm;
(2)由(1)可得n节链条长为:2.5n﹣0.8(n﹣1)=(1.7n+0.8)cm.
故答案为:(1.7n+0.8);
(3)1.7×50+0.8=85.8厘米,
所以50节这样的链条总长度是85.8厘米.
25、求代数式的值.
(1)已知:
,求的值;
(2)当时,求的值;
(3)已知:,求的值;
(4)与互为相反数,求代数式的值.
【答案】(1)3;(2);(3)13;(4)
【分析】(1)、(2)直接将字母的取值代入代数式即可求解;
(3)由,可先求出a的值,再将a、b的值代入代数式求解即可;
(4)由与互为相反数,可知,,从而可得,,然后将式子的值代入代数式即可求解.
【解析】
解:(1)当时,原式;
(2)当,原式;
(3)由得,原式;
(4)若与互为相反数,则;
因为;所以;;
原式,
故的值为.
阶段培优练习题(练习范围3.1-3.3字母表示数
代数式
代数式的值)
2021-2022学年苏科版七年级数学上册
一、选择题
1、用代数式表示:y与x的和的(
)
A.
B.
C.
D.
2、下列说法正确的是( )
A.多项式x2+2x2y+1是二次三项式
B.单项式2x2y的次数是2
C.0是单项式
D.单项式﹣3πx2y的系数是﹣3
3、下列说法中正确的个数是( )
(1)a和0都是单项式;
(2)多项式﹣3a2b+7a2b2﹣2ab+1是三次四项式;
(3)单项式的系数为﹣9;
(4)多项式x2+2xy﹣y2的项为x2、2xy、﹣y2.
A.1个
B.2个
C.3个
D.4个
4、下列说法中,正确的是( )
A.当x=2时,代数式x2+1的值是5
B.当a=3时,代数式a2﹣的值是12
C.当a=0时,代数式+1的值是1
D.代数式a2+b2的值恒为整数
5、若x﹣3y=﹣2,那么3﹣x+3y的值是( )
A.1
B.2
C.5
D.6
6、按图示的程序计算,若开始输入的x为正整数,最后输出的结果为67.则x的值可能是( )
A.3
B.7
C.12
D.23
7、当时,的值为18,则的值为(
)
A.40
B.42
C.46
D.56
8、把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形,,按此规律排列下去,则第⑧个图案中黑色三角形的个数为
A.10
B.18
C.21
D.36
9、下列各选项中,所列代数式错误的是(
).
A.表示“比a与b的积的2倍小5的数”的代数式是;
B.表示“a与b的平方差的相反数”的代数式;
C.表示“被5除商是a,余数是2的数”的代数式是;
D.表示“数a的一半与数b的3倍的差”的代数式是.
10、一个工程,甲独做要x小时,乙独做要y小时,两人合作3小时的工作量为(
)
A.3(x+y)
B.3()
C.
D.
二、填空题
11、下列代数式中①2 4,②,③x÷y,④x﹣2,其中书写正确的是_____.
12、如图,在一个长为b米,宽为a米的长方形草坪中间,有两条宽度都是c米的小径,则草地的总面积可表示为__________平方米.
13、(1)是五次单项式,则m= ;(2)若x2ym+1z2是五次单项式,则m= ;
(3)若xmyn+1z3是五次单项式,则2m+2n= ;(4)如果﹣5xym﹣2为四次单项式,则m= .
14、单项式的系数是 ,多项式2ab﹣3a2b2+1的次数是 .
15、已知,则代数式的值为________.
16、已知,,那么整式的值为_________.
17、a与b互为相反数,c与d互为倒数,m的绝对值为2,
则的值为_________.
18、如图所示是计算机程序计算,若开始输入,则最后输出的结果是 .
三、解答题
19、今年假期某校对操场进行了维修改造,如图是操场的一角.在长为a米,宽为b米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为c米.
(1)直接写出一个篮球场的长和宽;(用含字母a,b,c的代数式表示)
(2)用含字母a,b,c的代数式表示这两个篮球场占地面积的和,并求出当a=42,b=36,c=4时,这两个篮球场占地面积的和.
20、已知多项式(m﹣3)x|m|﹣2y3+x2y﹣2xy2是关于、y的四次三项式.
(1)求m的值;
(2)当x=,y=﹣1时,求此多项式的值.
21、观察下列单项式:﹣x,3x2,﹣5x3,7x4,…,﹣37x19,39x20,….
(1)这组单项式的系数的符号规律是
,系数的绝对值规律是
;
(2)这组单项式的次数的规律是
;
(3)根据上面的归纳,可以猜想第n个单项式是(只能填写一个代数式)
;
(4)请你根据猜想,写出第2008个、第2009个单项式,它们分别是
,
.
22、在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.如,当初始输入5时,即,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,
(1)当初始输入1时,第1次计算结果为
;
(2)当初始输入4时,第3次计算结果为
;
(3)当初始输入3时,依次计算得到的所有结果中,有 个不同的值,第20次计算结果为 .
23、国庆期间的某天上午,巡警小李驾驶巡逻车在南北走向的大道上巡逻.他8点整从派出所出发,开始巡逻.如果规定向南为正,他在这天上午行程记录如下(单位:千米):
+5,-13,+14,-15,+13,-12,-4,+10,+16,-14
(1)当巡逻结束时,小李是否回到了派出所?
(2)若巡逻车耗电量为千瓦时/千米,则这天上午巡逻车共耗电多少千瓦时?
24、如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)5节链条长
cm.
(2)n节链条长
cm.
(3)现有50节这样的链条,求链条总长为多少?
25、求代数式的值.
(1)已知:
,求的值;
(2)当时,求的值;
(3)已知:,求的值;
(4)与互为相反数,求代数式的值.
第三章
阶段培优练习题(练习范围3.1-3.3字母表示数
代数式
代数式的值)
2021-2022学年苏科版七年级数学上册(解析)
一、选择题
1、用代数式表示:y与x的和的(
)
A.
B.
C.
D.
【答案】A
【分析】y与x的和的,即为x与y先求和,然后再与相乘,据此列式即可.
【详解】解:y与x的和的,用代数式表示为.
故选:A.
2、下列说法正确的是( )
A.多项式x2+2x2y+1是二次三项式
B.单项式2x2y的次数是2
C.0是单项式
D.单项式﹣3πx2y的系数是﹣3
【分析】根据多项式、单项式、系数、常数项的定义分别进行判断,即可求出答案.
【解析】A.多项式x2+2x2y+1是三次三项式,此选项错误;
B.单项式2x2y的次数是3,此选项错误;
C.0是单项式,此选项正确;
D.单项式﹣3πx2y的系数是﹣3π,此选项错误;
故选:C.
3、下列说法中正确的个数是( )
(1)a和0都是单项式;
(2)多项式﹣3a2b+7a2b2﹣2ab+1是三次四项式;
(3)单项式的系数为﹣9;
(4)多项式x2+2xy﹣y2的项为x2、2xy、﹣y2.
A.1个
B.2个
C.3个
D.4个
【分析】根据单项式和多项式的相关定义解答即可.
【解析】(1)a和0都是单项式,原说法正确;
(2)多项式﹣3a2b+7a2b2﹣2ab+1是四次四项式,原说法错误;
(3)单项式的系数为,原说法错误;
(4)多项式x2+2xy﹣y2的项为x2、2xy、﹣y2,原说法正确.
说法中正确的个数是2个,
故选:B.
4、下列说法中,正确的是( )
A.当x=2时,代数式x2+1的值是5
B.当a=3时,代数式a2﹣的值是12
C.当a=0时,代数式+1的值是1
D.代数式a2+b2的值恒为整数
【分析】把字母的值代入代数式即可得到结论.
解:A、当x=2时,代数式x2+1的值是5,故正确;
B、当a=3时,代数式a2-
的值是5,故错误;
C、当a=0时,代数式
+1无意义,故错误;
D、代数式a2+b2的值恒为正数,故错误;
故选A.
5、若x﹣3y=﹣2,那么3﹣x+3y的值是( )
A.1
B.2
C.5
D.6
【分析】把x﹣3y=﹣2整体代入所求代数式求值即可.
【解析】当x﹣3y=﹣2时,原式=3﹣(x﹣3y)=3﹣(﹣2)=5.
故选:C.
6、按图示的程序计算,若开始输入的x为正整数,最后输出的结果为67.则x的值可能是( )
A.3
B.7
C.12
D.23
【分析】根据运算程序列出方程求得相应的x值,直到x不是正整数为止,然后对比选项即可得出答案.
【解析】∵最后输出的结果为67,∴3x+1=67,解得:x=22;
当3x+1=22时,解得:x=7;
当3x+1=7时,解得:x=2;
当3x+1=2时,解得:x=,
∵开始输入的x为正整数,
∴x=不合题意.
∴x的值可能为:2或7或22,
故选:B.
7、当时,的值为18,则的值为(
)
A.40
B.42
C.46
D.56
【答案】B
【分析】把代入计算结果18,变形后得,整体代入计算即可.
【解析】当时,,所以,所以,
则,
故选:B.
8、把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形,,按此规律排列下去,则第⑧个图案中黑色三角形的个数为
A.10
B.18
C.21
D.36
【分析】第①个图案中有1个黑色三角形,第②个图案中有个黑色三角形,第③个图案中有个黑色三角形,,按此规律排列下去,则第⑥个图案中黑色三角形的个数为个,结论可求.
【解答】解:第①个图案中有1个黑色三角形,
第②个图案中有个黑色三角形,
第③个图案中有个黑色三角形,
,
按此规律排列下去,则第⑧个图案中黑色三角形的个数为(个.
故选:.
9、下列各选项中,所列代数式错误的是(
).
A.表示“比a与b的积的2倍小5的数”的代数式是;
B.表示“a与b的平方差的相反数”的代数式;
C.表示“被5除商是a,余数是2的数”的代数式是;
D.表示“数a的一半与数b的3倍的差”的代数式是.
【答案】C
【分析】根据描述列出代数式进行判断即可.
【解析】
解:A、表示“比a与b的积的2倍小5的数”的代数式是,故此选项不符合题意;
B、表示“a与b的平方差的相反数”的代数式,故此选项不符合题意;
C、表示“被5除商是a,余数是2的数”的代数式是,故此选项符合题意;
D、表示“数a的一半与数b的3倍的差”的代数式是,故此选项不符合题意.
故选C.
10、一个工程,甲独做要x小时,乙独做要y小时,两人合作3小时的工作量为(
)
A.3(x+y)
B.3()
C.
D.
【答案】B
【解析】
【分析】根据甲、乙单独完成工作的时间,可以得到工作的效率,即可求解.
【解析】解:∵甲独做要x小时,乙独做要y小时
∴甲乙的工作效率分别为,所以合作三小时为3().
故选B.
二、填空题
11、下列代数式中①2 4,②,③x÷y,④x﹣2,其中书写正确的是_____.
【答案】④.
【解析】①2 4应为2×4;②x2应为x;③x÷y应为;④x-2书写正确,
综上所述,书写正确的是④.
12、如图,在一个长为b米,宽为a米的长方形草坪中间,有两条宽度都是c米的小径,则草地的总面积可表示为__________平方米.
【答案】
【分析】分别求出小径的面积和长方形的面积,再得出答案即可.
【详解】解:草地的总面积可表示为平方米,
故答案为:平方米.
13、(1)是五次单项式,则m= ;(2)若x2ym+1z2是五次单项式,则m= ;
(3)若xmyn+1z3是五次单项式,则2m+2n= ;(4)如果﹣5xym﹣2为四次单项式,则m= .
【分析】(1)直接利用单项式的次数确定方法分别分析得出答案;
(2)直接利用单项式的次数确定方法分别分析得出答案;
(3)直接利用单项式的次数确定方法分别分析得出答案;
(4)直接利用单项式的次数确定方法分别分析得出答案.
【解析】(1)∵是五次单项式,
∴2+m﹣1=5,
解得:m=4.故答案为:4;
(2)若x2ym+1z2是五次单项式,则2+m+1+2=5,
解得:m=0;故答案为:0;
(3)若xmyn+1z3是五次单项式,则m+n+1+3=5,
则m+n=1,
故2m+2n=2;故答案为:2;
(4)如果﹣5xym﹣2为四次单项式,则1+m﹣2=4,
解得:m=5.故答案为:5.
14、单项式的系数是 ,多项式2ab﹣3a2b2+1的次数是 .
【分析】利用单项式系数定义以及多项式的次数进行解答即可.
【解析】∵单项式中的数字因数叫做单项式的系数.
∴单项式系数是,
∵多项式中次数最高项的次数叫做多项式的次数.
∴多项式2ab﹣3a2b2+1的次数是4.
故答案为:,4.
15、已知,则代数式的值为________.
【答案】9
【分析】把所求代数式整理成已知条件的形式,然后代入进行计算即可求解.
【解析】解:∵,
∴
.
故答案为:
.
16、已知,,那么整式的值为_________.
【答案】14
【分析】先对代数式进行变形,然后利用整体代入进行求解即可.
【解析】
把作为整体代入,.
故答案为14
17、a与b互为相反数,c与d互为倒数,m的绝对值为2,
则的值为_________.
【答案】-11
【分析】根据a与b互为相反数,c与d互为倒数,m的绝对值为2,可得,,,将化简可得,根据当时,当时,分别求值即可.
【解析】解:∵a与b互为相反数,c与d互为倒数,m的绝对值为2,
∴,,,
∵
当时,,
当时,,
故答案是:-11.
18、如图所示是计算机程序计算,若开始输入,则最后输出的结果是 .
【分析】把的值代入程序中计算即可求出所求.
【解答】解:把代入程序得:,
把代入程序得:,
则最后输出的结果为.
故答案为:.
三、解答题
19、今年假期某校对操场进行了维修改造,如图是操场的一角.在长为a米,宽为b米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为c米.
(1)直接写出一个篮球场的长和宽;(用含字母a,b,c的代数式表示)
(2)用含字母a,b,c的代数式表示这两个篮球场占地面积的和,并求出当a=42,b=36,c=4时,这两个篮球场占地面积的和.
【解题思路】(1)根据题意求出两个长方形的长和宽,即可;
(2)把a=42,b=36,c=4代入(b﹣2c)(a﹣3c)求出即可.
【解答过程】(1)一个篮球场的长和宽分别为:(b﹣2c),(a﹣3c);
(2)这两个篮球场的占地面积为(b﹣2c)(a﹣3c)(平方米);
当a=42,b=36,c=4时,(42﹣4×3)×(36﹣2×4)=840(平方米).
20、已知多项式(m﹣3)x|m|﹣2y3+x2y﹣2xy2是关于、y的四次三项式.
(1)求m的值;
(2)当x=,y=﹣1时,求此多项式的值.
【分析】(1)直接利用多项式的次数的确定方法得出m的值;
(2)将x,y的值代入求出答案.
【解析】(1)∵多项式(m﹣3)x|m|﹣2y3+x2y﹣2xy2是关于xy的四次三项式,
∴|m|﹣2+3=4,m﹣3≠0,
解得:m=﹣3,
(2)当x=,y=﹣1时,此多项式的值为:
21、观察下列单项式:﹣x,3x2,﹣5x3,7x4,…,﹣37x19,39x20,….
(1)这组单项式的系数的符号规律是
,系数的绝对值规律是
;
(2)这组单项式的次数的规律是
;
(3)根据上面的归纳,可以猜想第n个单项式是(只能填写一个代数式)
;
(4)请你根据猜想,写出第2008个、第2009个单项式,它们分别是
,
.
【分析】所有式子均为单项式,先观察数字因数,可得规律:(﹣1)n(2n﹣1),再观察字母因数,可得规律:xn,然后代入求值即可.
【解析】(1)单项式的系数依次为:﹣1,3,﹣5,7,﹣9,11, ,为奇数且奇次项为负数,
可得规律:(﹣1)n(2n﹣1),
故答案为:(﹣1)n(或:负号正号依次出现),(2n﹣1);
(2)观察易知次数的规律为从1开始的连续自然数,
故答案为:从1开始的连续自然数;
(3)结合(1)和(2)可得第n个单项式为:(﹣1)n(2n﹣1)xn,
故答案为:(﹣1)n(2n﹣1)xn;
(4)把n=2008、n=2009直接代入(﹣1)n(2n﹣1)xn中,即可分别得到:4015x2008,﹣4017x2009,
故答案为:4015x2008,﹣4017x2009.
22、在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.如,当初始输入5时,即,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,
(1)当初始输入1时,第1次计算结果为
;
(2)当初始输入4时,第3次计算结果为
;
(3)当初始输入3时,依次计算得到的所有结果中,有 个不同的值,第20次计算结果为 .
【分析】(1)把代入指定的关系式求值即可;
(2)把代入指定的关系式计算第1次的结果,再根据结果的奇偶数,进行第2次运算,依此类推,求出第3次计算结果即可;
(3)把代入指定的关系式计算第1次的结果,再根据结果的奇偶数,进行第2次运算依此类推,发现其计算结果有规律,按照规律,求出第20次计算结果即可;
【解答】解:(1)当时,,故答案为:4;
(2)当时,第1次结果为:,第2次结果为,第3次结果为;
故答案为:4;
(3)当时,
第1次结果为:,
第2次结果为,
第3次结果为;
第4次结果为,
第5次结果为,
第6次结果为,
第7次结果为,
第8次结果为,
,第20次运算的结果为4.
有7个不同的值,
故答案为:7,4.
23、国庆期间的某天上午,巡警小李驾驶巡逻车在南北走向的大道上巡逻.他8点整从派出所出发,开始巡逻.如果规定向南为正,他在这天上午行程记录如下(单位:千米):
+5,-13,+14,-15,+13,-12,-4,+10,+16,-14
(1)当巡逻结束时,小李是否回到了派出所?
(2)若巡逻车耗电量为千瓦时/千米,则这天上午巡逻车共耗电多少千瓦时?
【答案】(1)回到了派出所;(2)千瓦时
【分析】(1)将所有数相加再对比即可得出答案;
(2)先将所有数的绝对值相加,再乘即可得出答案.
【详解】
解:(1)(千米).
答:小李回到了派出所.
(2)
(千米),
(千瓦时)
答:这天上午巡逻车共耗油千瓦时.
24、如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)5节链条长
cm.
(2)n节链条长
cm.
(3)现有50节这样的链条,求链条总长为多少?
【分析】(1)根据图形找出规律计算5节链条的长度即可;
(2)由(1)写出表示链条节数的一般式;
(3)根据(2)计算即可求解.
【解析】(1)根据图形可得出:
2节链条的长度为:2.5×2﹣0.8(cm),
3节链条的长度为:2.5×3﹣0.8×2(cm),
4节链条的长度为:2.5×4﹣0.8×3(cm),
5节链条的长度为:2.5×5﹣0.8×4=9.3(cm).
故答案为:9.3cm;
(2)由(1)可得n节链条长为:2.5n﹣0.8(n﹣1)=(1.7n+0.8)cm.
故答案为:(1.7n+0.8);
(3)1.7×50+0.8=85.8厘米,
所以50节这样的链条总长度是85.8厘米.
25、求代数式的值.
(1)已知:
,求的值;
(2)当时,求的值;
(3)已知:,求的值;
(4)与互为相反数,求代数式的值.
【答案】(1)3;(2);(3)13;(4)
【分析】(1)、(2)直接将字母的取值代入代数式即可求解;
(3)由,可先求出a的值,再将a、b的值代入代数式求解即可;
(4)由与互为相反数,可知,,从而可得,,然后将式子的值代入代数式即可求解.
【解析】
解:(1)当时,原式;
(2)当,原式;
(3)由得,原式;
(4)若与互为相反数,则;
因为;所以;;
原式,
故的值为.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
