22.3.1 几何图形问题-初中数学人教版九年级上册同步试题精编(Word版 含答案)
文档属性
| 名称 | 22.3.1 几何图形问题-初中数学人教版九年级上册同步试题精编(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 613.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览


文档简介
22.3几何图形问题
知识点1
图形面积问题
例1.某学校计划建一个长方形种植园,如图,种植园的一边靠墙,另三边用周长为30m的篱笆围成,已知墙长为18m,设这个种植园垂直于墙的一边长为x(m),种植园面积为y(m2).
(1)求与的函数关系式,并写出自变量的取值范围;
(2)根据实际需要,要求这个种植园的面积为100m2,求的值;
(3)当为多少m时,这个种植园的面积最大,并求出最大值.
变式2.用规格长为6m,宽为0.1m的铝合金型材,恰好制作成一个“日”字型窗子的边框(如图1,不计耗损),中间装长xm,宽ym完全一样的两张玻璃.这个窗子要装入最大边长为1.5m的正方形墙洞(如图2)中.
(1)求y与x之间的函数关系式,并求出x的取值范围.
(2)这个窗子的采光面积(两张玻璃面积之和)存在最大值吗?如果有,请求出来;如果没有,请说明理由.
3.如图,在边长为120cm的正方形铁皮ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体工艺盒(A,B,C,D四个顶点正好重合于上底面一点).已知点M,N在CD边上,且是被剪去的一个等腰直角三角形斜边的两个端点,设CM=DN=x(cm).
(1)若折成的包装盒恰好是个正方体,求这个工艺盒的体积;
(2)当x取何值时,工艺盒的四个侧面面积和S最大,最大值为多少?
课堂练习
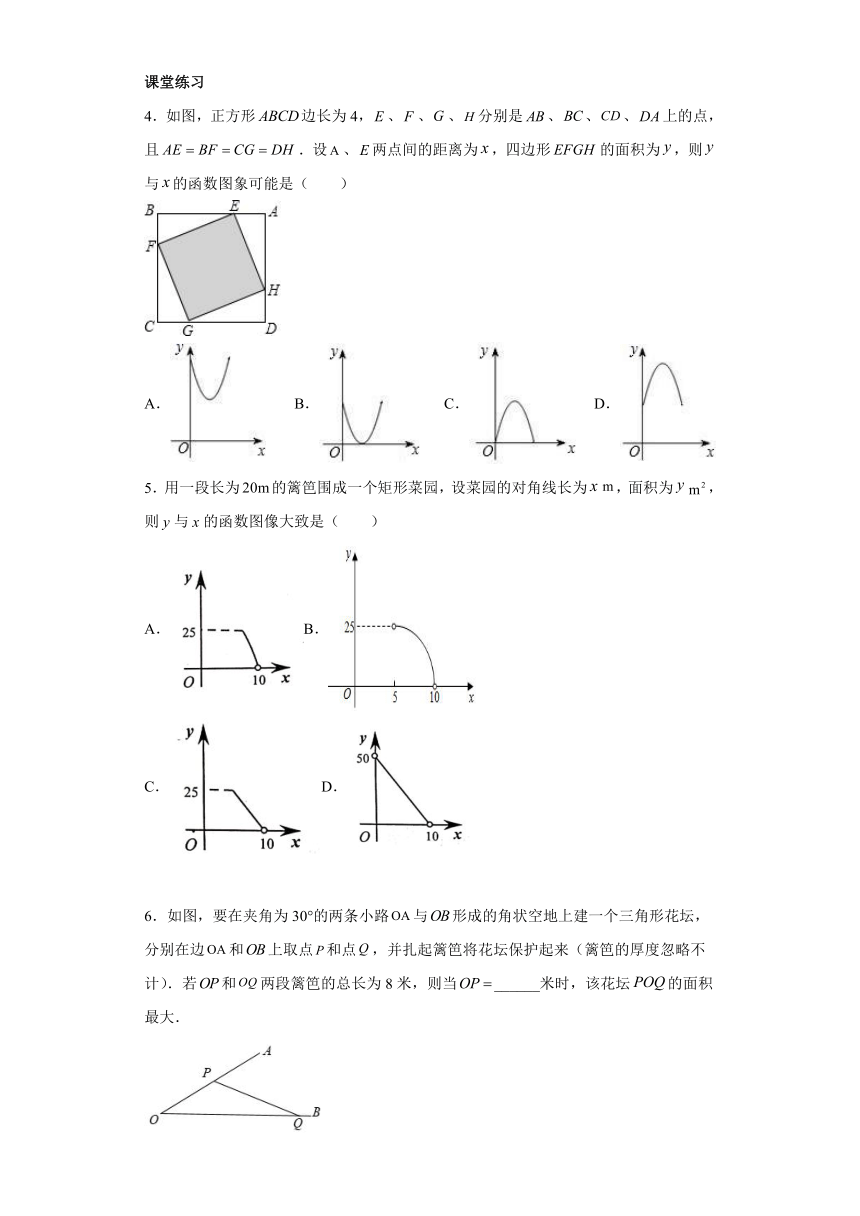
4.如图,正方形边长为4,、、、分别是、、、上的点,且.设、两点间的距离为,四边形的面积为,则与的函数图象可能是(
)
A.
B.
C.
D.
5.用一段长为的篱笆围成一个矩形菜园,设菜园的对角线长为,面积为,则y与x的函数图像大致是(
)
A.B.
C.D.
6.如图,要在夹角为30°的两条小路与形成的角状空地上建一个三角形花坛,分别在边和上取点和点,并扎起篱笆将花坛保护起来(篱笆的厚度忽略不计).若和两段篱笆的总长为8米,则当______米时,该花坛的面积最大.
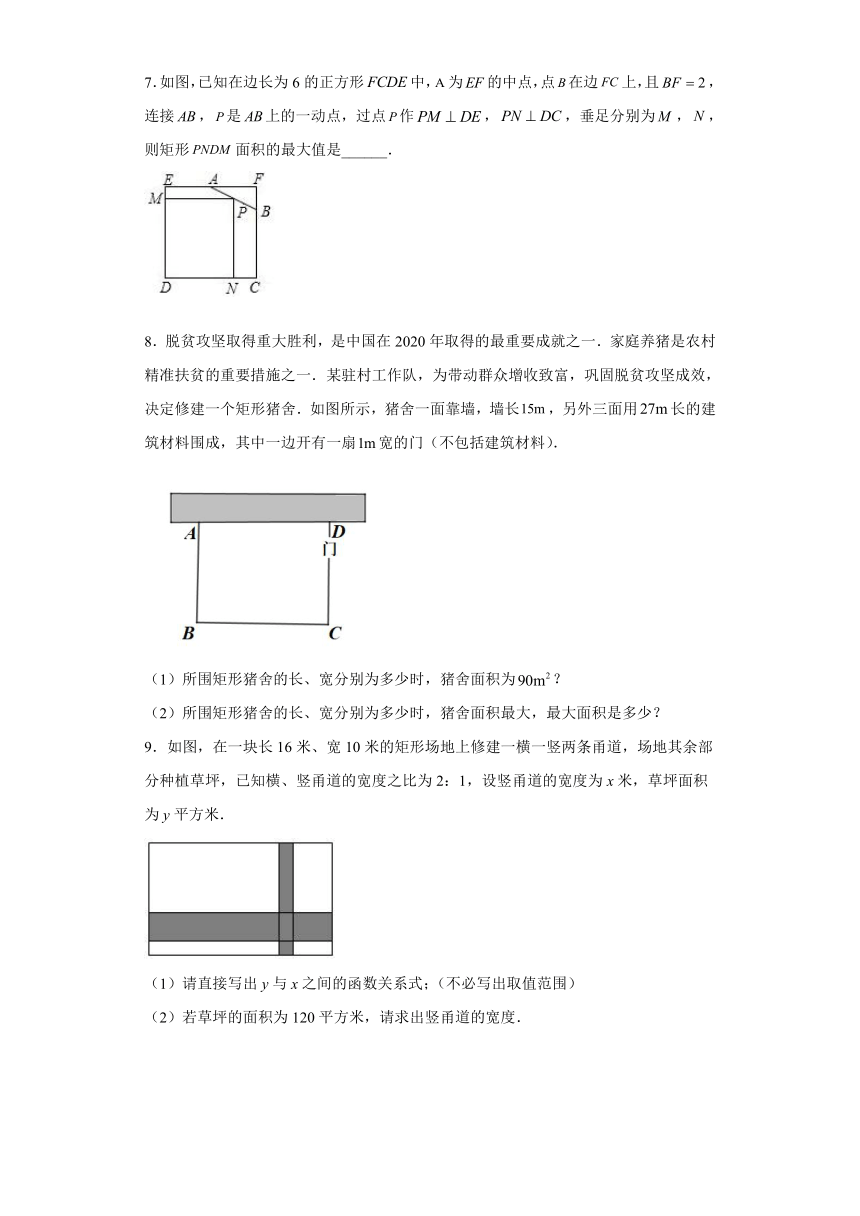
7.如图,已知在边长为6的正方形中,为的中点,点在边上,且,连接,是上的一动点,过点作,,垂足分别为,,则矩形面积的最大值是______.
8.脱贫攻坚取得重大胜利,是中国在2020年取得的最重要成就之一.家庭养猪是农村精准扶贫的重要措施之一.某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定修建一个矩形猪舍.如图所示,猪舍一面靠墙,墙长,另外三面用长的建筑材料围成,其中一边开有一扇宽的门(不包括建筑材料).
(1)所围矩形猪舍的长、宽分别为多少时,猪舍面积为?
(2)所围矩形猪舍的长、宽分别为多少时,猪舍面积最大,最大面积是多少?
9.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为x米,草坪面积为y平方米.
(1)请直接写出y与x之间的函数关系式;(不必写出取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
10.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长的篱笆围成一个矩形花园(篱笆只围两边),设.
(1)若花园的面积为,求的值;
(2)若在处有一棵树与墙的距离分别是和,要将这棵树围在花园(含边界,不考虑树的粗细),求花园面积的最大值.
11.某牧场准备利用现成的一堵“7”字型的墙面(如图中粗线表示墙面,已知,米,米)和总长为36米的篱笆围建一个“日”形的饲养场(细线表示篱笆,饲养场中间也是用篱笆隔开),如图,点可能在线段上,也可能在线段的延长线上.
(1)当点在线段上时,
①设的长为米,则______米(用含的代数式表示);
②若要求所围成的饲养场的面积为66平方米,求饲养场的宽;
(2)饲养场的宽为多少米时,饲养场的面积最大?最大面积为多少平方米?
12.小明的爸爸想在自家院子里用长为12米的篱笆围成一个矩形小花园,爸爸问小明,矩形的相邻两边长分别设计为多少米时小花园面积最大(不考虑接缝)?小明利用学习的《函数及其图象》知识探究如下,请将他的探究过程补充完整.
(1)(建立函数模型)由矩形的周长为12,设它的一边长为,面积为,则与之间的函数关系式为______,其中自变量的取值范围是______;
(2)(画出函数图象)
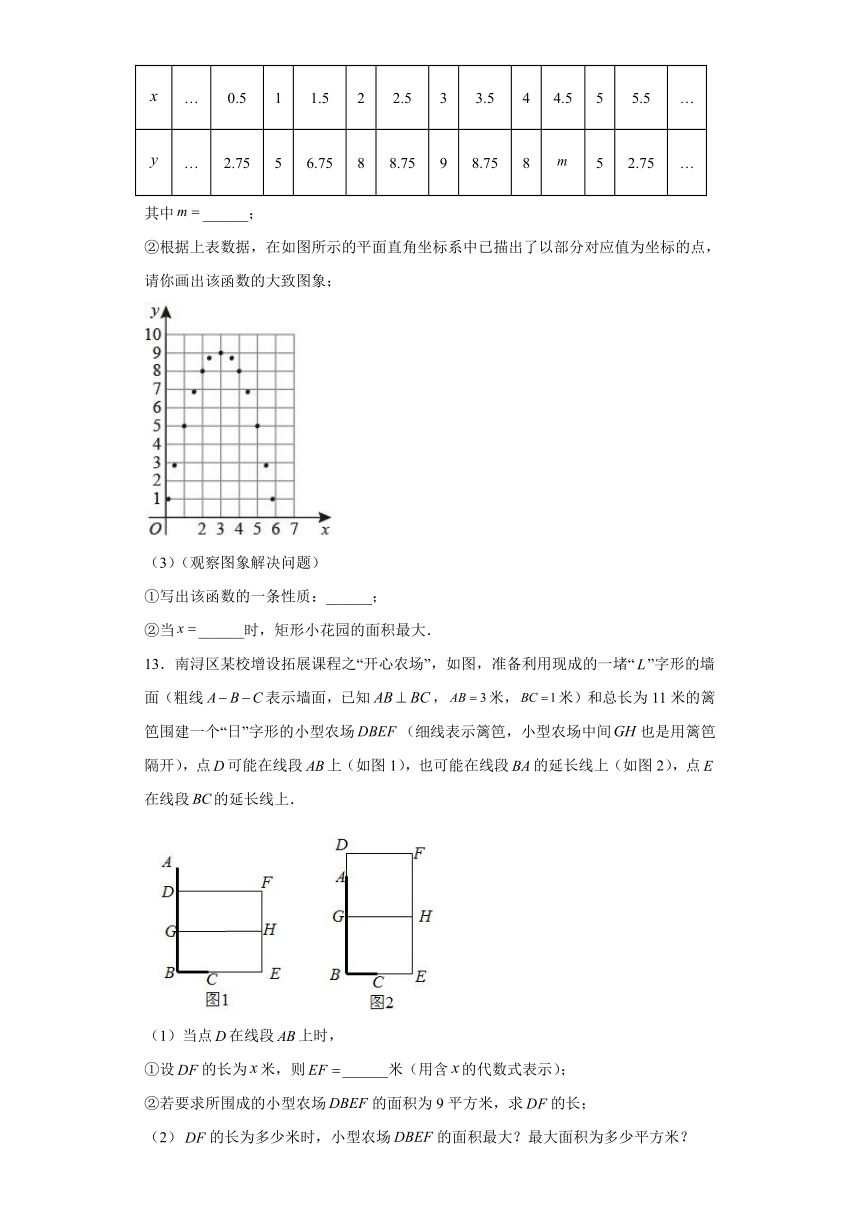
①与的几组对应值列表如下:
…
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
…
…
2.75
5
6.75
8
8.75
9
8.75
8
5
2.75
…
其中______;
②根据上表数据,在如图所示的平面直角坐标系中已描出了以部分对应值为坐标的点,请你画出该函数的大致图象;
(3)(观察图象解决问题)
①写出该函数的一条性质:______;
②当______时,矩形小花园的面积最大.
13.南浔区某校增设拓展课程之“开心农场”,如图,准备利用现成的一堵“”字形的墙面(粗线表示墙面,已知,米,米)和总长为11米的篱笆围建一个“日”字形的小型农场(细线表示篱笆,小型农场中间也是用篱笆隔开),点可能在线段上(如图1),也可能在线段的延长线上(如图2),点在线段的延长线上.
(1)当点在线段上时,
①设的长为米,则______米(用含的代数式表示);
②若要求所围成的小型农场的面积为9平方米,求的长;
(2)的长为多少米时,小型农场的面积最大?最大面积为多少平方米?
14.某公司承接项市政工程,制作一面景观墙,其形状是边长为9米的正方形,设计图案如下所示(四周阴影部分是四个全等的直角三角形,铺设绿植.中间是边长为整数的正方形,采用新能源涂料),两种材料单价如下表.设长为x米.
材料
绿植
新能源涂料
价格(元平方米)
100
200
(1)用含x的代数式表示使用新能源涂料的面积.
(2)该公司准备11040元用于采购上述两种材料,请你判断资金是否足够,并说明理由.
(3)为了推广环保施工,政府对新能源涂料提供每平方米m元的补贴,使得该公司投入11040元足以顺利完成材料采购,则m至少为_______元.(直接写出答案)
试卷第6页,总6页
参考答案
1.(1),;(2)10;(3)时,这个种植园的面积的最大值,最大面积为112.5m2
【分析】
(1)根据题意即可求得y与x的函数关系式为y=(30-2x)x;
(2)根据“种植园的面积为100m2”列出一元二次方程,解之可得;
(3)根据二次函数的最值问题,即可求得这个种植园的面积最大值.
【详解】
解:(1)根据题意得:,
∵,
∴
(2)由题意得:,
解得,,
∵,
∴时,这个种植园的面积为100.
(3)∵,,函数有最大值,
∴当时,这个种植园的面积的最大值,最大面积为.
【点睛】
本题主要考查了二次函数的实际应用问题,解决本题的关键是根据题意构建二次函数模型,然后根据二次函数的性质求解即可.
2.(1)y=﹣0.75x+1.35,1≤x≤1.3;(2)这个窗子的采光面积有最大值,最大值为1.2m2,见解析.
【分析】
(1)根据长方形的面积公式即可得到y和x的函数关系式;根据题意可得关于x的不等式组,解不等式组即可求出x的取值范围;
(2)设这个窗子的采光面积为Sm2,由(1)中的函数关系可知S和x是二次函数关系,根据二次函数的性质即可得到最大面积.
【详解】
解:(1)由题意,得3x+2(2y+0.1×3)=6,
整理,得3x+4y=5.4,
∴y=﹣0.75x+1.35,
∴y与x之间的函数关系式为y=﹣0.75x+1.35,
由题意,得,
解得1≤x≤1.3,
即x的取值范围是1≤x≤1.3;
(2)设这个窗子的采光面积为Sm2,
由题意,得S=2xy=2x(﹣0.75x+1.35)=﹣1.5x2+2.7x,
配方,得S=﹣1.5(x﹣0.9)2+1.215,
∵a=﹣1.5<0,对称轴为x=0.9,
∴当x>0.9时,y随x的增大而减小,
∵1≤x≤1.3,
∴当x=1时,S有最大值,
S最大=1.2,
答:这个窗子的采光面积有最大值,最大值为1.2m2.
【点睛】
本题考查的是长方形的面积公式及二次函数的最值问题,求出S与x的关系式是解答本题的关键.
3.(1)这个工艺盒的体积是5400cm3;(2)当x=30时,S最大,最大值为7200cm2.
【分析】
(1)先根据已知条件求得正方体的底面边长FG=GN=x,MN=GM=2x,再利用CD=120cm,求出x,最后求正方体的体积即可;
(2)先利用已知表示出工艺盒的侧面面积,进而利用二次函数求最值即可.
【详解】
解:(1)根据题意,设CM=DN=x(cm),折成的工艺盒恰好是个正方体,
由勾股定理可得:MG=GN=x,MN=2x
∵正方形纸片ABCD边长为120cm,即CM+MN+DN=120
∴x+2x+x=120,解得:x=30,
∴正方体的底面边长a=30,
∴V=a3==5400(cm3);
答:这个工艺盒的体积是5400cm3;
(2)设工艺盒的底面边长为acm,高为hcm,
则a=x,h==(60﹣x),
∴S=4ah=4x (60﹣x)=﹣8x2+480x=﹣8(x﹣30)2+7200,
∵0<x<60,
∴当x=30时,S最大,最大值为7200cm2.
【点睛】
本题主要考查了二次函数的应用,将实际问题转化成函数问题是解答本题的关键.
4.A
【分析】
本题考查了动点的函数图象,先判定图中的四个小直角三角形全等,再用大正方形的面积减去四个直角三角形的面积,得函数y的表达式,结合选项的图象可得答案.
【详解】
解:∵正方形ABCD边长为4,AE=BF=CG=DH
∴AH=BE=CF=DG,∠A=∠B=∠C=∠D
∴△AEH≌△BFE≌△CGF≌△DHG
∴y=4×4-x(4-x)×4
=16-8x+2x2
=2(x-2)2+8
∴y是x的二次函数,函数的顶点坐标为(2,8),开口向上,
从4个选项来看,开口向上的只有A和B,C和D图象开口向下,不符合题意;
但是B的顶点在x轴上,故B不符合题意,只有A符合题意.
故选:A.
【点睛】
本题考查了动点问题的函数图象,正确地写出函数解析式并数形结合分析是解题的关键.
5.B
【分析】
设矩形的长为am,宽为bm,根据矩形的性质可得a+b=10,根据勾股定理可得a、b、x的关系,从而得出y与x的函数关系式,然后问题可求解.
【详解】
解:设矩形的长为am,宽为bm,由题意得:,
∵菜园的对角线长为,
∴,
∴a2+(10-a)2=x2,
整理,得2a2-20a+100=x2,
易得≤x<10,
∵(a+b)2=a2+2ab+b2,
∴102=x2+2ab,
∴,
∴0≤y<25,且x=时,y=25,
∴y与x函数图象是二次函数的图象,即开口向下的抛物线;
故选B.
【点睛】
本题主要考查二次函数的实际应用,熟练掌握二次函数的图象与性质是解题的关键.
6.4
【分析】
设OP=x,则OQ=8-x,过点P作PM⊥OQ,,由30°角所对的直角边等于斜边的一半可得PM=,根据三角形面积公式可得面积关于OQ的二次函数,配方后即可求解.
【详解】
解:设OP=x,则OQ=8-x,
过点P作PM⊥OQ,交OQ于点M,如图,
∵
∴
∴
∵
∴函数图象开口向下,有最大值,为4,
故当OP=4时,花坛的面积最大.
故答案为:4.
【点睛】
此题主要考查了二次函数的应用,利用面积法求出二次函数关系式是解答此题的关键.
7.24
【分析】
以FE为x轴,以FC为y轴,先建立平面直角坐标系,求出A
B的解析式为,设P(a,),用含a的式子表示出PM,PN,根据矩形面积公式列式,根据二次函数的性质即可求解.
【详解】
解:以FE为x轴,以FC为y轴,建立平面直角坐标系,
∵边长为6的正方形中,为的中点,,
∴A(-3,0),B(0,-2),C(0,-6),E(-6,0),
设A
B的解析式为,则
,解得,
∴(),
设P(a,)(),则PM=6+a,PN=,
∴,
∴当a=0时,矩形面积的最大值是24.
故答案为:24.
【点睛】
本题考查了二次函数的应用问题,用待定系数法求一次函数的解析式,矩形的面积,正方形的性质等知识点,能灵活运用知识点是解此题的关键.
8.(1)所围矩形猪舍的长为,宽为时,猪舍的面积为;(2)所围矩形猪舍的长为,宽为时,面积最大,最大面积是.
【分析】
(1)设,则,根据题意列式即可;
(2)设,所围矩形猪圈的面积为,列出二次函数计算即可;
【详解】
解:(1)设,则.
根据题意可得:,
解得:,.
当时,,不符合题意,舍去;
当时,,符合题意.
答:所围矩形猪舍的长为,宽为时,猪舍的面积为.
(2)设,所围矩形猪圈的面积为.
,
.
当,时,.
答:所围矩形猪舍的长为,宽为时,面积最大,最大面积是.
【点睛】
本题主要考查了二次函数与一元二次方程的应用,准确计算是解题的关键.
9.(1)y=2x2﹣42x+160;(2)竖甬道的宽度为1米.
【分析】
(1)设竖甬道的宽度为x米,草坪面积为y平方米,则横甬道的宽度为2x米,剩余部分可合成长(16﹣x)米,宽(10﹣2x)米的矩形,即可写出y与x之间的函数关系式;
(2)由(1)把
代入函数关系式,然后解一元二次方程即可求解.
【详解】
解:(1)设竖甬道的宽度为x米,草坪面积为y平方米,则横甬道的宽度为2x米,剩余部分可合成长(16﹣x)米,宽(10﹣2x)米的矩形,
依题意得:y=(16﹣x)(10﹣2x)=2x2﹣42x+160.
(2)依题意得:2x2﹣42x+160=120,
整理得:x2﹣21x+20=0,
解得:x1=1,x2=20.
当x=1时,10﹣2x=10﹣2×1=8>0,符合题意;
当x=20时,10﹣2x=10﹣2×20=﹣30<0,不符合题意,舍去.
答:竖甬道的宽度为1米.
【点睛】
本题主要考查了列函数关系式和解一元二次方程,解题的关键是理解题意,列出函数关系式.
10.(1)11或17;(2)192平方米
【分析】
(1)根据题意得出长×宽=187,进而得出答案;
(2)由题意可得出:S=x(28-x)=-x2+28x=-(x-14)2+196,再利用二次函数增减性求得最值.
【详解】
解:(1)∵AB=xm,则BC=(28-x)m,
∴x(28-x)=187,
解得:x1=11,x2=17,
答:x的值为11m或17m;
(2)∵AB=xm,
∴BC=28-x,
∴S=x(28-x)=-x2+28x=-(x-14)2+196,
∵在P处有一棵树与墙CD,AD的距离分别是16m和6m,
∵28-x≥16,x≥6
∴6≤x≤12,
∴当x=12时,S取到最大值为:S=-(12-14)2+196=192,
答:花园面积S的最大值为192平方米.
【点睛】
此题主要考查了二次函数的应用以及二次函数最值求法,得出S与x的函数关系式是解题关键.
11.(1)①;②饲养场的宽为11米;(2)饲养场的宽为8米时,饲养场的面积最大,最大面积为96平方米.
【分析】
(1)①根据矩形的性质求出GH和DB的长度,进而求出AD的长度,再根据篱笆总长度为36米,做减法即可求出DE的长度.
②根据矩形的面积公式列出一元二次方程并求解即可.
(2)根据题意,对点F是在线段BC上还是在线段BC的延长线上进行分类讨论,然后根据矩形的面积公式列出饲养场BDEF的面积S与EF的长度x的关系式,再根据二次函数的性质求出当x为何值时,S取到最大值.
【详解】
解:(1)①∵饲养场BDEF是一个“日”形,
∴四边形BDEF是由矩形BDGH和矩形FEGH组成的矩形.
∴DE=BF,DB=GH=EF.
∵EF=x,
∴DB=GH=EF=x.
又∵AB=3,
∴.
∴.
∴.
故答案为:().
②∵要求所围成的饲养场的面积为66平方米,
∴.
∴.
解得,,
∵点在线段上,且BC=9,
∴,即.
解得.
∴x=11,即饲养场的宽为11米.
答:饲养场的宽为11米.
(2)设饲养场的面积为,的长为米.
①当点在线段上时,
根据(1)可得:,
∵,
∴当时,有最大值,最大值为,且当时,随的增大而减小.
∵当点在线段上时,需满足,
∴时,有最大值,最大值为(平方米).
此时,满足点F在线段BC上.
②当点在线段的延长线上时,设DE为y米,
由(1)可得DB=GH=EF=x,DE=BF=y,,
∵BC=9,
∴.
∴.
∴.
解得.
∴.
∴.
∵,
∴当时,有最大值,最大值为(平方米).
此时,满足点F在线段BC的延长线上.
∵,
∴饲养场的宽为8米时,饲养场的面积最大,最大面积为96平方米.
答:饲养场的宽为8米时,饲养场的面积最大,最大面积为96平方米.
【点睛】
本题考查一元二次方程的应用和二次函数的应用,把实际问题抽象成数学问题并列出方程或关系式是解题关键,同时根据题目实际情况要注意分类讨论和实际意义.
12.(1),;(2)①6.75;②见解析;(3)①当时,随的增大而增大;②3
【分析】
(1)根据题意和矩形的面积表示方法即可求得.
(2)①当x=4.5时,代入表达式即可求得.②用平滑的曲线把每个点连起来即可.
(3)①由图像可知当x<3时的增减性.②由图像可知面积最大时x的取值.
【详解】
解:(1),.
(2)①6.75.
②函数图象如图所示:
(3)①当时,随的增大而增大;
②3.
【点睛】
此题考查了二次函数应用题表达式的求法,二次函数图像和性质的关系.解题的关键是熟练掌握二次函数表达式的求法,二次函数图像和性质的关系.
13.(1)①;②3米;(2)当米时,最大为平方米
【分析】
(1)①根据题意用篱笆总长度为11米,减去DF、GH、CE的长度,即可求得EF的长度;
②小型农场形状为矩形,面积,解出x的值即可;
(2)设小型农场的面积为S,求出关于EF的长的函数关系式,根据二次函数的性质即可解答.
【详解】
解(1)①
②
,解得,
∵点在线段上,,
舍去,.
(2)当点在线段上时,即,时
,∴当时,最大为9.
当点在线段的延长线上时,
即时,
当时,最大为.
∴综上所述,当时,最大为.
【点睛】
此题主要考查的是二次函数的应用,一元二次方程的应用,掌握矩形的面积计算方法是解题的关键.
14.(1);(2)不够,理由见解析;(3)40
【分析】
(1)利用x表示各边长,利用勾股定理得到,即可得出结果;
(2)求出总费用为,利用二次函数的性质求出EF最小值为7时,总费用最小,从而得到,代入二次函数表达式求出总费用的最小值,再比较即可;
(3)根据(2)中结果得到不等式,解之即可.
【详解】
解:(1)∵四个阴影部分直角三角形全等,
∴,,
在中,由勾股定理得:
,
∴正方形EFGH面积,
故使用新能源涂料的面积为.
(2)铺设绿植面积为:,
∴铺设绿植费用为:,
新能源涂料费用为:,
∴总费用为:,
关于的二次函数图象开口向上,对称轴为直线,
当时,函数值随增大而增大,当时,函数值随增大而减小,
当时,,
又,为整数,
∴EF最小值为7,即EF取最小值时,总费用最小,
∴,
即,
∴,
∴总费用最少为,
故资金11040不够.
(3)由(2)可知时使用资金最少,为13000元,
∴,
∴,
故至少为40.
【点睛】
本题考查了二次函数的实际应用,解题的关键是理解题意,列出函数表达式,注意题中正方形边长为整数.
答案第13页,总13页
知识点1
图形面积问题
例1.某学校计划建一个长方形种植园,如图,种植园的一边靠墙,另三边用周长为30m的篱笆围成,已知墙长为18m,设这个种植园垂直于墙的一边长为x(m),种植园面积为y(m2).
(1)求与的函数关系式,并写出自变量的取值范围;
(2)根据实际需要,要求这个种植园的面积为100m2,求的值;
(3)当为多少m时,这个种植园的面积最大,并求出最大值.
变式2.用规格长为6m,宽为0.1m的铝合金型材,恰好制作成一个“日”字型窗子的边框(如图1,不计耗损),中间装长xm,宽ym完全一样的两张玻璃.这个窗子要装入最大边长为1.5m的正方形墙洞(如图2)中.
(1)求y与x之间的函数关系式,并求出x的取值范围.
(2)这个窗子的采光面积(两张玻璃面积之和)存在最大值吗?如果有,请求出来;如果没有,请说明理由.
3.如图,在边长为120cm的正方形铁皮ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体工艺盒(A,B,C,D四个顶点正好重合于上底面一点).已知点M,N在CD边上,且是被剪去的一个等腰直角三角形斜边的两个端点,设CM=DN=x(cm).
(1)若折成的包装盒恰好是个正方体,求这个工艺盒的体积;
(2)当x取何值时,工艺盒的四个侧面面积和S最大,最大值为多少?
课堂练习
4.如图,正方形边长为4,、、、分别是、、、上的点,且.设、两点间的距离为,四边形的面积为,则与的函数图象可能是(
)
A.
B.
C.
D.
5.用一段长为的篱笆围成一个矩形菜园,设菜园的对角线长为,面积为,则y与x的函数图像大致是(
)
A.B.
C.D.
6.如图,要在夹角为30°的两条小路与形成的角状空地上建一个三角形花坛,分别在边和上取点和点,并扎起篱笆将花坛保护起来(篱笆的厚度忽略不计).若和两段篱笆的总长为8米,则当______米时,该花坛的面积最大.
7.如图,已知在边长为6的正方形中,为的中点,点在边上,且,连接,是上的一动点,过点作,,垂足分别为,,则矩形面积的最大值是______.
8.脱贫攻坚取得重大胜利,是中国在2020年取得的最重要成就之一.家庭养猪是农村精准扶贫的重要措施之一.某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定修建一个矩形猪舍.如图所示,猪舍一面靠墙,墙长,另外三面用长的建筑材料围成,其中一边开有一扇宽的门(不包括建筑材料).
(1)所围矩形猪舍的长、宽分别为多少时,猪舍面积为?
(2)所围矩形猪舍的长、宽分别为多少时,猪舍面积最大,最大面积是多少?
9.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为x米,草坪面积为y平方米.
(1)请直接写出y与x之间的函数关系式;(不必写出取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
10.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长的篱笆围成一个矩形花园(篱笆只围两边),设.
(1)若花园的面积为,求的值;
(2)若在处有一棵树与墙的距离分别是和,要将这棵树围在花园(含边界,不考虑树的粗细),求花园面积的最大值.
11.某牧场准备利用现成的一堵“7”字型的墙面(如图中粗线表示墙面,已知,米,米)和总长为36米的篱笆围建一个“日”形的饲养场(细线表示篱笆,饲养场中间也是用篱笆隔开),如图,点可能在线段上,也可能在线段的延长线上.
(1)当点在线段上时,
①设的长为米,则______米(用含的代数式表示);
②若要求所围成的饲养场的面积为66平方米,求饲养场的宽;
(2)饲养场的宽为多少米时,饲养场的面积最大?最大面积为多少平方米?
12.小明的爸爸想在自家院子里用长为12米的篱笆围成一个矩形小花园,爸爸问小明,矩形的相邻两边长分别设计为多少米时小花园面积最大(不考虑接缝)?小明利用学习的《函数及其图象》知识探究如下,请将他的探究过程补充完整.
(1)(建立函数模型)由矩形的周长为12,设它的一边长为,面积为,则与之间的函数关系式为______,其中自变量的取值范围是______;
(2)(画出函数图象)
①与的几组对应值列表如下:
…
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
…
…
2.75
5
6.75
8
8.75
9
8.75
8
5
2.75
…
其中______;
②根据上表数据,在如图所示的平面直角坐标系中已描出了以部分对应值为坐标的点,请你画出该函数的大致图象;
(3)(观察图象解决问题)
①写出该函数的一条性质:______;
②当______时,矩形小花园的面积最大.
13.南浔区某校增设拓展课程之“开心农场”,如图,准备利用现成的一堵“”字形的墙面(粗线表示墙面,已知,米,米)和总长为11米的篱笆围建一个“日”字形的小型农场(细线表示篱笆,小型农场中间也是用篱笆隔开),点可能在线段上(如图1),也可能在线段的延长线上(如图2),点在线段的延长线上.
(1)当点在线段上时,
①设的长为米,则______米(用含的代数式表示);
②若要求所围成的小型农场的面积为9平方米,求的长;
(2)的长为多少米时,小型农场的面积最大?最大面积为多少平方米?
14.某公司承接项市政工程,制作一面景观墙,其形状是边长为9米的正方形,设计图案如下所示(四周阴影部分是四个全等的直角三角形,铺设绿植.中间是边长为整数的正方形,采用新能源涂料),两种材料单价如下表.设长为x米.
材料
绿植
新能源涂料
价格(元平方米)
100
200
(1)用含x的代数式表示使用新能源涂料的面积.
(2)该公司准备11040元用于采购上述两种材料,请你判断资金是否足够,并说明理由.
(3)为了推广环保施工,政府对新能源涂料提供每平方米m元的补贴,使得该公司投入11040元足以顺利完成材料采购,则m至少为_______元.(直接写出答案)
试卷第6页,总6页
参考答案
1.(1),;(2)10;(3)时,这个种植园的面积的最大值,最大面积为112.5m2
【分析】
(1)根据题意即可求得y与x的函数关系式为y=(30-2x)x;
(2)根据“种植园的面积为100m2”列出一元二次方程,解之可得;
(3)根据二次函数的最值问题,即可求得这个种植园的面积最大值.
【详解】
解:(1)根据题意得:,
∵,
∴
(2)由题意得:,
解得,,
∵,
∴时,这个种植园的面积为100.
(3)∵,,函数有最大值,
∴当时,这个种植园的面积的最大值,最大面积为.
【点睛】
本题主要考查了二次函数的实际应用问题,解决本题的关键是根据题意构建二次函数模型,然后根据二次函数的性质求解即可.
2.(1)y=﹣0.75x+1.35,1≤x≤1.3;(2)这个窗子的采光面积有最大值,最大值为1.2m2,见解析.
【分析】
(1)根据长方形的面积公式即可得到y和x的函数关系式;根据题意可得关于x的不等式组,解不等式组即可求出x的取值范围;
(2)设这个窗子的采光面积为Sm2,由(1)中的函数关系可知S和x是二次函数关系,根据二次函数的性质即可得到最大面积.
【详解】
解:(1)由题意,得3x+2(2y+0.1×3)=6,
整理,得3x+4y=5.4,
∴y=﹣0.75x+1.35,
∴y与x之间的函数关系式为y=﹣0.75x+1.35,
由题意,得,
解得1≤x≤1.3,
即x的取值范围是1≤x≤1.3;
(2)设这个窗子的采光面积为Sm2,
由题意,得S=2xy=2x(﹣0.75x+1.35)=﹣1.5x2+2.7x,
配方,得S=﹣1.5(x﹣0.9)2+1.215,
∵a=﹣1.5<0,对称轴为x=0.9,
∴当x>0.9时,y随x的增大而减小,
∵1≤x≤1.3,
∴当x=1时,S有最大值,
S最大=1.2,
答:这个窗子的采光面积有最大值,最大值为1.2m2.
【点睛】
本题考查的是长方形的面积公式及二次函数的最值问题,求出S与x的关系式是解答本题的关键.
3.(1)这个工艺盒的体积是5400cm3;(2)当x=30时,S最大,最大值为7200cm2.
【分析】
(1)先根据已知条件求得正方体的底面边长FG=GN=x,MN=GM=2x,再利用CD=120cm,求出x,最后求正方体的体积即可;
(2)先利用已知表示出工艺盒的侧面面积,进而利用二次函数求最值即可.
【详解】
解:(1)根据题意,设CM=DN=x(cm),折成的工艺盒恰好是个正方体,
由勾股定理可得:MG=GN=x,MN=2x
∵正方形纸片ABCD边长为120cm,即CM+MN+DN=120
∴x+2x+x=120,解得:x=30,
∴正方体的底面边长a=30,
∴V=a3==5400(cm3);
答:这个工艺盒的体积是5400cm3;
(2)设工艺盒的底面边长为acm,高为hcm,
则a=x,h==(60﹣x),
∴S=4ah=4x (60﹣x)=﹣8x2+480x=﹣8(x﹣30)2+7200,
∵0<x<60,
∴当x=30时,S最大,最大值为7200cm2.
【点睛】
本题主要考查了二次函数的应用,将实际问题转化成函数问题是解答本题的关键.
4.A
【分析】
本题考查了动点的函数图象,先判定图中的四个小直角三角形全等,再用大正方形的面积减去四个直角三角形的面积,得函数y的表达式,结合选项的图象可得答案.
【详解】
解:∵正方形ABCD边长为4,AE=BF=CG=DH
∴AH=BE=CF=DG,∠A=∠B=∠C=∠D
∴△AEH≌△BFE≌△CGF≌△DHG
∴y=4×4-x(4-x)×4
=16-8x+2x2
=2(x-2)2+8
∴y是x的二次函数,函数的顶点坐标为(2,8),开口向上,
从4个选项来看,开口向上的只有A和B,C和D图象开口向下,不符合题意;
但是B的顶点在x轴上,故B不符合题意,只有A符合题意.
故选:A.
【点睛】
本题考查了动点问题的函数图象,正确地写出函数解析式并数形结合分析是解题的关键.
5.B
【分析】
设矩形的长为am,宽为bm,根据矩形的性质可得a+b=10,根据勾股定理可得a、b、x的关系,从而得出y与x的函数关系式,然后问题可求解.
【详解】
解:设矩形的长为am,宽为bm,由题意得:,
∵菜园的对角线长为,
∴,
∴a2+(10-a)2=x2,
整理,得2a2-20a+100=x2,
易得≤x<10,
∵(a+b)2=a2+2ab+b2,
∴102=x2+2ab,
∴,
∴0≤y<25,且x=时,y=25,
∴y与x函数图象是二次函数的图象,即开口向下的抛物线;
故选B.
【点睛】
本题主要考查二次函数的实际应用,熟练掌握二次函数的图象与性质是解题的关键.
6.4
【分析】
设OP=x,则OQ=8-x,过点P作PM⊥OQ,,由30°角所对的直角边等于斜边的一半可得PM=,根据三角形面积公式可得面积关于OQ的二次函数,配方后即可求解.
【详解】
解:设OP=x,则OQ=8-x,
过点P作PM⊥OQ,交OQ于点M,如图,
∵
∴
∴
∵
∴函数图象开口向下,有最大值,为4,
故当OP=4时,花坛的面积最大.
故答案为:4.
【点睛】
此题主要考查了二次函数的应用,利用面积法求出二次函数关系式是解答此题的关键.
7.24
【分析】
以FE为x轴,以FC为y轴,先建立平面直角坐标系,求出A
B的解析式为,设P(a,),用含a的式子表示出PM,PN,根据矩形面积公式列式,根据二次函数的性质即可求解.
【详解】
解:以FE为x轴,以FC为y轴,建立平面直角坐标系,
∵边长为6的正方形中,为的中点,,
∴A(-3,0),B(0,-2),C(0,-6),E(-6,0),
设A
B的解析式为,则
,解得,
∴(),
设P(a,)(),则PM=6+a,PN=,
∴,
∴当a=0时,矩形面积的最大值是24.
故答案为:24.
【点睛】
本题考查了二次函数的应用问题,用待定系数法求一次函数的解析式,矩形的面积,正方形的性质等知识点,能灵活运用知识点是解此题的关键.
8.(1)所围矩形猪舍的长为,宽为时,猪舍的面积为;(2)所围矩形猪舍的长为,宽为时,面积最大,最大面积是.
【分析】
(1)设,则,根据题意列式即可;
(2)设,所围矩形猪圈的面积为,列出二次函数计算即可;
【详解】
解:(1)设,则.
根据题意可得:,
解得:,.
当时,,不符合题意,舍去;
当时,,符合题意.
答:所围矩形猪舍的长为,宽为时,猪舍的面积为.
(2)设,所围矩形猪圈的面积为.
,
.
当,时,.
答:所围矩形猪舍的长为,宽为时,面积最大,最大面积是.
【点睛】
本题主要考查了二次函数与一元二次方程的应用,准确计算是解题的关键.
9.(1)y=2x2﹣42x+160;(2)竖甬道的宽度为1米.
【分析】
(1)设竖甬道的宽度为x米,草坪面积为y平方米,则横甬道的宽度为2x米,剩余部分可合成长(16﹣x)米,宽(10﹣2x)米的矩形,即可写出y与x之间的函数关系式;
(2)由(1)把
代入函数关系式,然后解一元二次方程即可求解.
【详解】
解:(1)设竖甬道的宽度为x米,草坪面积为y平方米,则横甬道的宽度为2x米,剩余部分可合成长(16﹣x)米,宽(10﹣2x)米的矩形,
依题意得:y=(16﹣x)(10﹣2x)=2x2﹣42x+160.
(2)依题意得:2x2﹣42x+160=120,
整理得:x2﹣21x+20=0,
解得:x1=1,x2=20.
当x=1时,10﹣2x=10﹣2×1=8>0,符合题意;
当x=20时,10﹣2x=10﹣2×20=﹣30<0,不符合题意,舍去.
答:竖甬道的宽度为1米.
【点睛】
本题主要考查了列函数关系式和解一元二次方程,解题的关键是理解题意,列出函数关系式.
10.(1)11或17;(2)192平方米
【分析】
(1)根据题意得出长×宽=187,进而得出答案;
(2)由题意可得出:S=x(28-x)=-x2+28x=-(x-14)2+196,再利用二次函数增减性求得最值.
【详解】
解:(1)∵AB=xm,则BC=(28-x)m,
∴x(28-x)=187,
解得:x1=11,x2=17,
答:x的值为11m或17m;
(2)∵AB=xm,
∴BC=28-x,
∴S=x(28-x)=-x2+28x=-(x-14)2+196,
∵在P处有一棵树与墙CD,AD的距离分别是16m和6m,
∵28-x≥16,x≥6
∴6≤x≤12,
∴当x=12时,S取到最大值为:S=-(12-14)2+196=192,
答:花园面积S的最大值为192平方米.
【点睛】
此题主要考查了二次函数的应用以及二次函数最值求法,得出S与x的函数关系式是解题关键.
11.(1)①;②饲养场的宽为11米;(2)饲养场的宽为8米时,饲养场的面积最大,最大面积为96平方米.
【分析】
(1)①根据矩形的性质求出GH和DB的长度,进而求出AD的长度,再根据篱笆总长度为36米,做减法即可求出DE的长度.
②根据矩形的面积公式列出一元二次方程并求解即可.
(2)根据题意,对点F是在线段BC上还是在线段BC的延长线上进行分类讨论,然后根据矩形的面积公式列出饲养场BDEF的面积S与EF的长度x的关系式,再根据二次函数的性质求出当x为何值时,S取到最大值.
【详解】
解:(1)①∵饲养场BDEF是一个“日”形,
∴四边形BDEF是由矩形BDGH和矩形FEGH组成的矩形.
∴DE=BF,DB=GH=EF.
∵EF=x,
∴DB=GH=EF=x.
又∵AB=3,
∴.
∴.
∴.
故答案为:().
②∵要求所围成的饲养场的面积为66平方米,
∴.
∴.
解得,,
∵点在线段上,且BC=9,
∴,即.
解得.
∴x=11,即饲养场的宽为11米.
答:饲养场的宽为11米.
(2)设饲养场的面积为,的长为米.
①当点在线段上时,
根据(1)可得:,
∵,
∴当时,有最大值,最大值为,且当时,随的增大而减小.
∵当点在线段上时,需满足,
∴时,有最大值,最大值为(平方米).
此时,满足点F在线段BC上.
②当点在线段的延长线上时,设DE为y米,
由(1)可得DB=GH=EF=x,DE=BF=y,,
∵BC=9,
∴.
∴.
∴.
解得.
∴.
∴.
∵,
∴当时,有最大值,最大值为(平方米).
此时,满足点F在线段BC的延长线上.
∵,
∴饲养场的宽为8米时,饲养场的面积最大,最大面积为96平方米.
答:饲养场的宽为8米时,饲养场的面积最大,最大面积为96平方米.
【点睛】
本题考查一元二次方程的应用和二次函数的应用,把实际问题抽象成数学问题并列出方程或关系式是解题关键,同时根据题目实际情况要注意分类讨论和实际意义.
12.(1),;(2)①6.75;②见解析;(3)①当时,随的增大而增大;②3
【分析】
(1)根据题意和矩形的面积表示方法即可求得.
(2)①当x=4.5时,代入表达式即可求得.②用平滑的曲线把每个点连起来即可.
(3)①由图像可知当x<3时的增减性.②由图像可知面积最大时x的取值.
【详解】
解:(1),.
(2)①6.75.
②函数图象如图所示:
(3)①当时,随的增大而增大;
②3.
【点睛】
此题考查了二次函数应用题表达式的求法,二次函数图像和性质的关系.解题的关键是熟练掌握二次函数表达式的求法,二次函数图像和性质的关系.
13.(1)①;②3米;(2)当米时,最大为平方米
【分析】
(1)①根据题意用篱笆总长度为11米,减去DF、GH、CE的长度,即可求得EF的长度;
②小型农场形状为矩形,面积,解出x的值即可;
(2)设小型农场的面积为S,求出关于EF的长的函数关系式,根据二次函数的性质即可解答.
【详解】
解(1)①
②
,解得,
∵点在线段上,,
舍去,.
(2)当点在线段上时,即,时
,∴当时,最大为9.
当点在线段的延长线上时,
即时,
当时,最大为.
∴综上所述,当时,最大为.
【点睛】
此题主要考查的是二次函数的应用,一元二次方程的应用,掌握矩形的面积计算方法是解题的关键.
14.(1);(2)不够,理由见解析;(3)40
【分析】
(1)利用x表示各边长,利用勾股定理得到,即可得出结果;
(2)求出总费用为,利用二次函数的性质求出EF最小值为7时,总费用最小,从而得到,代入二次函数表达式求出总费用的最小值,再比较即可;
(3)根据(2)中结果得到不等式,解之即可.
【详解】
解:(1)∵四个阴影部分直角三角形全等,
∴,,
在中,由勾股定理得:
,
∴正方形EFGH面积,
故使用新能源涂料的面积为.
(2)铺设绿植面积为:,
∴铺设绿植费用为:,
新能源涂料费用为:,
∴总费用为:,
关于的二次函数图象开口向上,对称轴为直线,
当时,函数值随增大而增大,当时,函数值随增大而减小,
当时,,
又,为整数,
∴EF最小值为7,即EF取最小值时,总费用最小,
∴,
即,
∴,
∴总费用最少为,
故资金11040不够.
(3)由(2)可知时使用资金最少,为13000元,
∴,
∴,
故至少为40.
【点睛】
本题考查了二次函数的实际应用,解题的关键是理解题意,列出函数表达式,注意题中正方形边长为整数.
答案第13页,总13页
同课章节目录
