22.3.3 抛物线形问题-初中数学人教版九年级上册同步试题精编(Word版 含答案)
文档属性
| 名称 | 22.3.3 抛物线形问题-初中数学人教版九年级上册同步试题精编(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 417.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 11:03:36 | ||
图片预览




文档简介
22.3抛物线形问题
一、选择题
1.某公园有一个圆形喷水池,喷出的水流呈抛物线状,一条水流的高度与水流时间之间的解析式为,那么水流从抛出至落到地面所需要的时间是(
)
A.
B.
C.
D.
2.如图是抛物线型拱桥,当拱顶离水面时,水面宽.若水面再下降,水面宽度为(
).
A.
B.
C.
D.
3.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t=;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③
B.①②③
C.①②③④
D.②③④
二、填空题
4.为了在体育中考中取得更好的成绩,小明积极训练,体育老师对小明投掷铅球的录像进行技术分析,如图,发现铅球在行进过程中高度y(m)与水平距离x(m)之间的关系为,由此可知小明此次投掷的成绩是___.
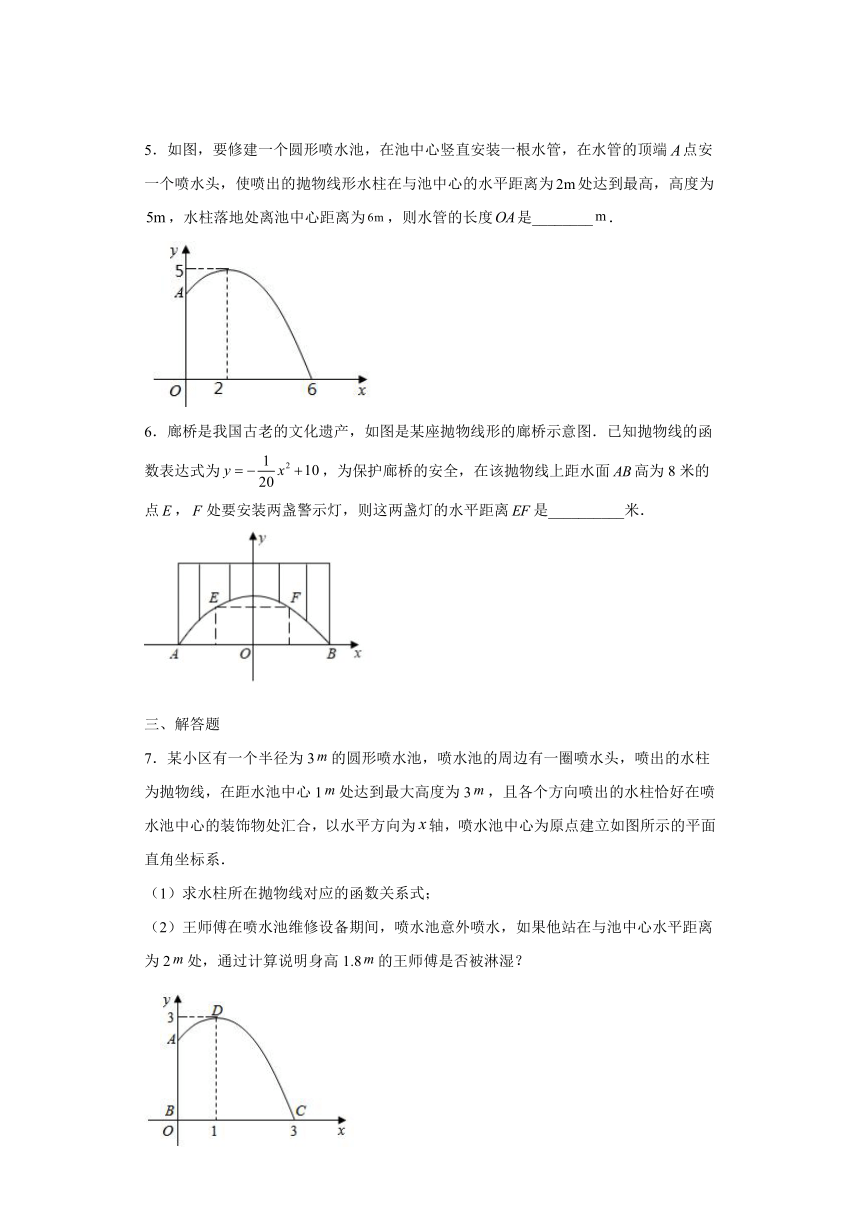
5.如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端点安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心距离为,则水管的长度是________.
6.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为8米的点,处要安装两盏警示灯,则这两盏灯的水平距离是__________米.
三、解答题
7.某小区有一个半径为3的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心1处达到最大高度为3,且各个方向喷出的水柱恰好在喷水池中心的装饰物处汇合,以水平方向为轴,喷水池中心为原点建立如图所示的平面直角坐标系.
(1)求水柱所在抛物线对应的函数关系式;
(2)王师傅在喷水池维修设备期间,喷水池意外喷水,如果他站在与池中心水平距离为2处,通过计算说明身高1.8的王师傅是否被淋湿?
8.公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的表达式为且过顶点(长度单位:m).
(1)直接写出c的值;
(2)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H,G分别在抛物线上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求点G的坐标.
9.如图是某公园一喷水池(示意图),在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25.
(1)求喷出的水流离地面的最大高度;
(2)求喷嘴离地面的高度;
(3)若把喷水池改成圆形,则水池半径至少为多少时,才能使喷出的水流不落在水池外?
10.已知,足球球门高米,宽米(如图1)在射门训练中,一球员接传球后射门,击球点A距离地面米,即米,球的运动路线是抛物线的一部分,当球的水平移动距离为6米时,球恰好到达最高点D,即米.以直线为x轴,以直线为y轴建立平面直角坐标系(如图2).
(1)求该抛物线的表达式;
(2)若足球恰好击中球门横梁,求该足球运动的水平距离;
(3)若要使球直接落在球门内,则该球员应后退m米后接球射门,击球点为(如图3),请直接写出m的取值范围.
11.在一次篮球比赛中,如图,队员甲正在投篮.已知球出手时离地面,与篮圈中心的水平距离为,球出手后水平距离为时达到最大高度,设篮球运行轨迹为抛物线,篮圈距地面.
(1)建立如图所示的平面直角坐标系,求此抛物线的解析式;
(2)此时球能否准确投中?
(3)此时,对方队员乙在甲面前处跳起盖帽拦截,已知乙的最大摸高为,那么他能否获得成功?
12.一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
试卷第4页,总4页
参考答案
1.B
【分析】
求出解析中h=0时t的值即可得.
【详解】
在h=30t 5t2中,令h=0可得30t 5t2=0,
解得:t=0或t=6,
所以水流从抛出至落到地面所需要的时间是6s,
故选:B.
【点睛】
本题主要考查二次函数的应用,解题的关键是明确解析式中水流落到地面所对应的函数值为0.
2.D
【分析】
以AB所在直线为x轴,以过拱顶C且垂直于AB的直线为y轴,建立平面直角坐标系,由待定系数法求得二次函数的解析式,然后由题意得关于x的一元二次方程,解得x的值,用较大的x值减去较小的x值即可得出答案.
【详解】
解:如图,以AB所在直线为x轴,以过拱顶C且垂直于AB的直线为y轴,建立平面直角坐标系,
则由题意可知A(-2,0),B(2,0),C(0,2),
设该抛物线的解析式为y=ax2+2,将B(2,0)代入得:
0=a×4+2,
解得:a=-.
∴抛物线的解析式为y=-x2+2,
∴若水面再下降1.5m,则有-1.5=-x2+2,
解得:x=±.
∵-(-)=2,
∴水面宽度为2m.
故选:D.
【点睛】
本题考查了二次函数在实际问题中的应用,明确二次函数的性质是解题的关键.
3.C
【分析】
由题意,抛物线经过(0,0),(9,0),所以可以假设抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,可得h=﹣t2+9t=﹣(t﹣4.5)2+20.25,由此即可一一判断.
【详解】
解:由题意,抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
∴h=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m>20m,故①正确,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,h=0,
∴点(9,0)在该抛物线上,故③正确,
∵当t=5时,h=20,当t=7时,h=14,
∴足球被踢出5s~7s时,距离地面的高度逐渐下降,故④正确.
∴正确的有①②③④,
故选:C.
【点睛】
本题考查二次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用二次函数的性质解答.
4.7m
【分析】
当y=0时代入解析式,求出x的值就可以求出结论.
【详解】
解:由题意,得
当y=0时,,
化简,得:,
解得:(舍去),
故答案为:7m.
【点睛】
本题考查了二次函数的应用,一元二次方程的解法,解题关键是结合题意,取函数或者自变量的特殊值列方程求解.
5.
【分析】
设抛物线解析式为y=a(x-h)2+k,将(2,5)与(6,0)代入解析式,求得a的值,再令x=0,求得y的值,即可得出答案.
【详解】
解:设抛物线解析式为y=a(x-h)2+k,
由题意可知抛物线的顶点为(2,5),与x轴的一个交点为(6,0),
∴0=a(6-2)2+5,解得:,
∴抛物线解析式为:
当x=0时,
∴水管的长度OA是m.
故答案为:.
【点睛】
本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握待定系数法是解题的关键.
6.
【分析】
根据题意可知E、F两点是关于y轴对称的,且纵坐标都为8,则代入解析式可分别求解出两点的横坐标,从而计算出EF的长度.
【详解】
由题,E、F两点是关于y轴对称,纵坐标都为8,代入解析式,
∴,解得:,,
∴,
故答案为:.
【点睛】
本题考查二次函数的实际应用,仔细观察图形并理解题意,准确建立并求解方程是解题关键.
7.(1)(0<x<3);(2)不会被淋湿,理由见解析
【分析】
(1)根据顶点坐标可设二次函数的顶点式,代入点(3,0),求出a值,此题得解;
(2)利用二次函数图象上点的坐标特征,求出当时的函数值,由此即可得出结论.
【详解】
(1)设水柱所在抛物线(第一象限部分)的函数表达式为(a≠0),
将(3,0)代入,得:4a+3=0,
解得:,
∴水柱所在抛物线的函数表达式为(0<x<3).
(2)当时,有,
∵
∴不会被淋湿.
【点睛】
本题考查的知识点是二次函数的实际应用,掌握二次函数的图象及其性质是解此题的关键.
8.(1)的值为5;(2).
【分析】
(1)把顶点坐标代入解析式即可确定c的值;
(2)用点G的坐标分别表示EF,FG的长,后根据矩形EFGH的周长,构造一元二次方程求解即可.
【详解】
(1)由抛物线的表达式为,
∵点在抛物线上,
∴的值为5;
(2)设,
∴矩形的周长,
∴,
把m=5代入==3.75;
∴的坐标为(5,3.75).
【点睛】
本题考查了二次函数的实际应用,矩形的周长,用坐标表示线段的长,利用数形结合思想,把矩形的周长转化为点的坐标为未知数的一元二次方程是解题的关键.
9.(1)喷出的水流离地面的最大高度为2.25m;(2)水池半径至少为2.5m时,才能使喷出的水流不落在水池.
【分析】
(1)直接利用二次函数解析式得出水流离地面的最大高度;
(2)利用x=0求出y的值即可;
(3)利用y=0求出x的值,进而得出答案.
【详解】
解:(1)∵水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25,
∴喷出的水流离地面的最大高度为:2.25m;
(2)当x=0,则y=-(0-1)2+2.25=1.25(m),
答:喷嘴离地面的高度为1.25m;
(3)由题意可得:y=0时,0=-(x-1)2+2.25,
解得:x1=-0.5(舍去),,x2=2.5,
答:水池半径至少为2.5m时,才能使喷出的水流不落在水池外.
【点睛】
本题主要考查了二次函数的应用,根据题意得出x=0以及y=0的意义是解题关键.
10.(1);(2)10.2米;(3)
【分析】
(1)根据条件可以得到抛物线的顶点坐标是(6,4.4),利用待定系数法即可求得函数的解析式;
(2)求出当y=2.44时x的值,再检验即得答案;
(3)先求出y=0时,x的值,取正,减去恰好击中球门横梁时,足球的水平距离即可.
【详解】
解:(1)抛物线的顶点坐标是,
设抛物线的解析式是:,
把代入得,
解得,
则抛物线是;
(2)球门高为2.44米,即,
则有,
解得:,,
从题干图2中,发现球门在右边,
,
即足球运动的水平距离是10.2米;
(3)不后退时,刚好击中横梁,
往后退,则球可以进入球门,
而当球落地时,球刚好在门口,是一个临界值,
当时,
有,
解得:,,
取正值,,
后退的距离需小于米
故.
【点睛】
本题考查了待定系数法求二次函数的解析式,以及二次函数的应用,正确求得解析式是关键.
11.(1);(2)能投中;(3)能拦截成功,理由见解析
【分析】
(1)根据抛物线的顶点坐标及球出手时的坐标,可确定抛物线的解析式;
(2)令x=7,求出y的值,与3m比较即可作出判断;
(3)将x=1代入进而得出答案.
【详解】
(1)
如图,球出手点、最高点(顶点)坐标分别为:,
设二次函数解析式为,将点代入可得:,
解得:,抛物线解析式为:;
(2)将点横坐标代入抛物线解析式得:
即点在抛物线上,此球一定能投中;
(3)能拦截成功.理由:将代入得
,他能拦截成功.
【点睛】
本题考查了二次函数解析式的求法,及其实际应用.此题为数学建模题,借助二次函数解决实际问题.
12.(1)y=-x2+4;(2)能安全通过,见解析;(3)n=4时,L有最大值,最大值为14
【分析】
(1)根据题意和函数图象,可以设出抛物线的解析式,然后根据抛物线过点F和点M即可求得该抛物线的解析式;
(2)先求出抛物线的解析式,再根据题意判断该隧道能通过的车辆的最高高度,便可判断该车辆能安全通过.
(3)射出H的坐标,用n表示出L,利用二次函数的性质求解即可.
【详解】
解:(1)由题意得M(0,4),F(4,0)
可设抛物线的解析式为y=ax2+4,
将F(4,0)代入y=ax2+4中,得a=-,
∴抛物线的解析式为y=-x2+4;
(2)当x=3,y=,
+2-=3.253.2,∴能安全通过;
(3)由GH=n,可设H(),
∴GH+GA+BH=n+()×2+2×2=,
∴L=,
∵a<0,抛物线开口向下,
∴当n=-=4时,L有最大值,最大值为14.
【点睛】
本题考查了二次函数的实际应用,解题的关键是要注意自变量的取值范围必须使实际问题有意义.
答案第8页,总8页
一、选择题
1.某公园有一个圆形喷水池,喷出的水流呈抛物线状,一条水流的高度与水流时间之间的解析式为,那么水流从抛出至落到地面所需要的时间是(
)
A.
B.
C.
D.
2.如图是抛物线型拱桥,当拱顶离水面时,水面宽.若水面再下降,水面宽度为(
).
A.
B.
C.
D.
3.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t=;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③
B.①②③
C.①②③④
D.②③④
二、填空题
4.为了在体育中考中取得更好的成绩,小明积极训练,体育老师对小明投掷铅球的录像进行技术分析,如图,发现铅球在行进过程中高度y(m)与水平距离x(m)之间的关系为,由此可知小明此次投掷的成绩是___.
5.如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端点安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心距离为,则水管的长度是________.
6.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为8米的点,处要安装两盏警示灯,则这两盏灯的水平距离是__________米.
三、解答题
7.某小区有一个半径为3的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心1处达到最大高度为3,且各个方向喷出的水柱恰好在喷水池中心的装饰物处汇合,以水平方向为轴,喷水池中心为原点建立如图所示的平面直角坐标系.
(1)求水柱所在抛物线对应的函数关系式;
(2)王师傅在喷水池维修设备期间,喷水池意外喷水,如果他站在与池中心水平距离为2处,通过计算说明身高1.8的王师傅是否被淋湿?
8.公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的表达式为且过顶点(长度单位:m).
(1)直接写出c的值;
(2)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H,G分别在抛物线上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求点G的坐标.
9.如图是某公园一喷水池(示意图),在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25.
(1)求喷出的水流离地面的最大高度;
(2)求喷嘴离地面的高度;
(3)若把喷水池改成圆形,则水池半径至少为多少时,才能使喷出的水流不落在水池外?
10.已知,足球球门高米,宽米(如图1)在射门训练中,一球员接传球后射门,击球点A距离地面米,即米,球的运动路线是抛物线的一部分,当球的水平移动距离为6米时,球恰好到达最高点D,即米.以直线为x轴,以直线为y轴建立平面直角坐标系(如图2).
(1)求该抛物线的表达式;
(2)若足球恰好击中球门横梁,求该足球运动的水平距离;
(3)若要使球直接落在球门内,则该球员应后退m米后接球射门,击球点为(如图3),请直接写出m的取值范围.
11.在一次篮球比赛中,如图,队员甲正在投篮.已知球出手时离地面,与篮圈中心的水平距离为,球出手后水平距离为时达到最大高度,设篮球运行轨迹为抛物线,篮圈距地面.
(1)建立如图所示的平面直角坐标系,求此抛物线的解析式;
(2)此时球能否准确投中?
(3)此时,对方队员乙在甲面前处跳起盖帽拦截,已知乙的最大摸高为,那么他能否获得成功?
12.一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
试卷第4页,总4页
参考答案
1.B
【分析】
求出解析中h=0时t的值即可得.
【详解】
在h=30t 5t2中,令h=0可得30t 5t2=0,
解得:t=0或t=6,
所以水流从抛出至落到地面所需要的时间是6s,
故选:B.
【点睛】
本题主要考查二次函数的应用,解题的关键是明确解析式中水流落到地面所对应的函数值为0.
2.D
【分析】
以AB所在直线为x轴,以过拱顶C且垂直于AB的直线为y轴,建立平面直角坐标系,由待定系数法求得二次函数的解析式,然后由题意得关于x的一元二次方程,解得x的值,用较大的x值减去较小的x值即可得出答案.
【详解】
解:如图,以AB所在直线为x轴,以过拱顶C且垂直于AB的直线为y轴,建立平面直角坐标系,
则由题意可知A(-2,0),B(2,0),C(0,2),
设该抛物线的解析式为y=ax2+2,将B(2,0)代入得:
0=a×4+2,
解得:a=-.
∴抛物线的解析式为y=-x2+2,
∴若水面再下降1.5m,则有-1.5=-x2+2,
解得:x=±.
∵-(-)=2,
∴水面宽度为2m.
故选:D.
【点睛】
本题考查了二次函数在实际问题中的应用,明确二次函数的性质是解题的关键.
3.C
【分析】
由题意,抛物线经过(0,0),(9,0),所以可以假设抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,可得h=﹣t2+9t=﹣(t﹣4.5)2+20.25,由此即可一一判断.
【详解】
解:由题意,抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
∴h=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m>20m,故①正确,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,h=0,
∴点(9,0)在该抛物线上,故③正确,
∵当t=5时,h=20,当t=7时,h=14,
∴足球被踢出5s~7s时,距离地面的高度逐渐下降,故④正确.
∴正确的有①②③④,
故选:C.
【点睛】
本题考查二次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用二次函数的性质解答.
4.7m
【分析】
当y=0时代入解析式,求出x的值就可以求出结论.
【详解】
解:由题意,得
当y=0时,,
化简,得:,
解得:(舍去),
故答案为:7m.
【点睛】
本题考查了二次函数的应用,一元二次方程的解法,解题关键是结合题意,取函数或者自变量的特殊值列方程求解.
5.
【分析】
设抛物线解析式为y=a(x-h)2+k,将(2,5)与(6,0)代入解析式,求得a的值,再令x=0,求得y的值,即可得出答案.
【详解】
解:设抛物线解析式为y=a(x-h)2+k,
由题意可知抛物线的顶点为(2,5),与x轴的一个交点为(6,0),
∴0=a(6-2)2+5,解得:,
∴抛物线解析式为:
当x=0时,
∴水管的长度OA是m.
故答案为:.
【点睛】
本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握待定系数法是解题的关键.
6.
【分析】
根据题意可知E、F两点是关于y轴对称的,且纵坐标都为8,则代入解析式可分别求解出两点的横坐标,从而计算出EF的长度.
【详解】
由题,E、F两点是关于y轴对称,纵坐标都为8,代入解析式,
∴,解得:,,
∴,
故答案为:.
【点睛】
本题考查二次函数的实际应用,仔细观察图形并理解题意,准确建立并求解方程是解题关键.
7.(1)(0<x<3);(2)不会被淋湿,理由见解析
【分析】
(1)根据顶点坐标可设二次函数的顶点式,代入点(3,0),求出a值,此题得解;
(2)利用二次函数图象上点的坐标特征,求出当时的函数值,由此即可得出结论.
【详解】
(1)设水柱所在抛物线(第一象限部分)的函数表达式为(a≠0),
将(3,0)代入,得:4a+3=0,
解得:,
∴水柱所在抛物线的函数表达式为(0<x<3).
(2)当时,有,
∵
∴不会被淋湿.
【点睛】
本题考查的知识点是二次函数的实际应用,掌握二次函数的图象及其性质是解此题的关键.
8.(1)的值为5;(2).
【分析】
(1)把顶点坐标代入解析式即可确定c的值;
(2)用点G的坐标分别表示EF,FG的长,后根据矩形EFGH的周长,构造一元二次方程求解即可.
【详解】
(1)由抛物线的表达式为,
∵点在抛物线上,
∴的值为5;
(2)设,
∴矩形的周长,
∴,
把m=5代入==3.75;
∴的坐标为(5,3.75).
【点睛】
本题考查了二次函数的实际应用,矩形的周长,用坐标表示线段的长,利用数形结合思想,把矩形的周长转化为点的坐标为未知数的一元二次方程是解题的关键.
9.(1)喷出的水流离地面的最大高度为2.25m;(2)水池半径至少为2.5m时,才能使喷出的水流不落在水池.
【分析】
(1)直接利用二次函数解析式得出水流离地面的最大高度;
(2)利用x=0求出y的值即可;
(3)利用y=0求出x的值,进而得出答案.
【详解】
解:(1)∵水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25,
∴喷出的水流离地面的最大高度为:2.25m;
(2)当x=0,则y=-(0-1)2+2.25=1.25(m),
答:喷嘴离地面的高度为1.25m;
(3)由题意可得:y=0时,0=-(x-1)2+2.25,
解得:x1=-0.5(舍去),,x2=2.5,
答:水池半径至少为2.5m时,才能使喷出的水流不落在水池外.
【点睛】
本题主要考查了二次函数的应用,根据题意得出x=0以及y=0的意义是解题关键.
10.(1);(2)10.2米;(3)
【分析】
(1)根据条件可以得到抛物线的顶点坐标是(6,4.4),利用待定系数法即可求得函数的解析式;
(2)求出当y=2.44时x的值,再检验即得答案;
(3)先求出y=0时,x的值,取正,减去恰好击中球门横梁时,足球的水平距离即可.
【详解】
解:(1)抛物线的顶点坐标是,
设抛物线的解析式是:,
把代入得,
解得,
则抛物线是;
(2)球门高为2.44米,即,
则有,
解得:,,
从题干图2中,发现球门在右边,
,
即足球运动的水平距离是10.2米;
(3)不后退时,刚好击中横梁,
往后退,则球可以进入球门,
而当球落地时,球刚好在门口,是一个临界值,
当时,
有,
解得:,,
取正值,,
后退的距离需小于米
故.
【点睛】
本题考查了待定系数法求二次函数的解析式,以及二次函数的应用,正确求得解析式是关键.
11.(1);(2)能投中;(3)能拦截成功,理由见解析
【分析】
(1)根据抛物线的顶点坐标及球出手时的坐标,可确定抛物线的解析式;
(2)令x=7,求出y的值,与3m比较即可作出判断;
(3)将x=1代入进而得出答案.
【详解】
(1)
如图,球出手点、最高点(顶点)坐标分别为:,
设二次函数解析式为,将点代入可得:,
解得:,抛物线解析式为:;
(2)将点横坐标代入抛物线解析式得:
即点在抛物线上,此球一定能投中;
(3)能拦截成功.理由:将代入得
,他能拦截成功.
【点睛】
本题考查了二次函数解析式的求法,及其实际应用.此题为数学建模题,借助二次函数解决实际问题.
12.(1)y=-x2+4;(2)能安全通过,见解析;(3)n=4时,L有最大值,最大值为14
【分析】
(1)根据题意和函数图象,可以设出抛物线的解析式,然后根据抛物线过点F和点M即可求得该抛物线的解析式;
(2)先求出抛物线的解析式,再根据题意判断该隧道能通过的车辆的最高高度,便可判断该车辆能安全通过.
(3)射出H的坐标,用n表示出L,利用二次函数的性质求解即可.
【详解】
解:(1)由题意得M(0,4),F(4,0)
可设抛物线的解析式为y=ax2+4,
将F(4,0)代入y=ax2+4中,得a=-,
∴抛物线的解析式为y=-x2+4;
(2)当x=3,y=,
+2-=3.253.2,∴能安全通过;
(3)由GH=n,可设H(),
∴GH+GA+BH=n+()×2+2×2=,
∴L=,
∵a<0,抛物线开口向下,
∴当n=-=4时,L有最大值,最大值为14.
【点睛】
本题考查了二次函数的实际应用,解题的关键是要注意自变量的取值范围必须使实际问题有意义.
答案第8页,总8页
同课章节目录
