23.1.2 旋转作图-初中数学人教版九年级上册同步试题精编(Word版 含答案)
文档属性
| 名称 | 23.1.2 旋转作图-初中数学人教版九年级上册同步试题精编(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 384.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览

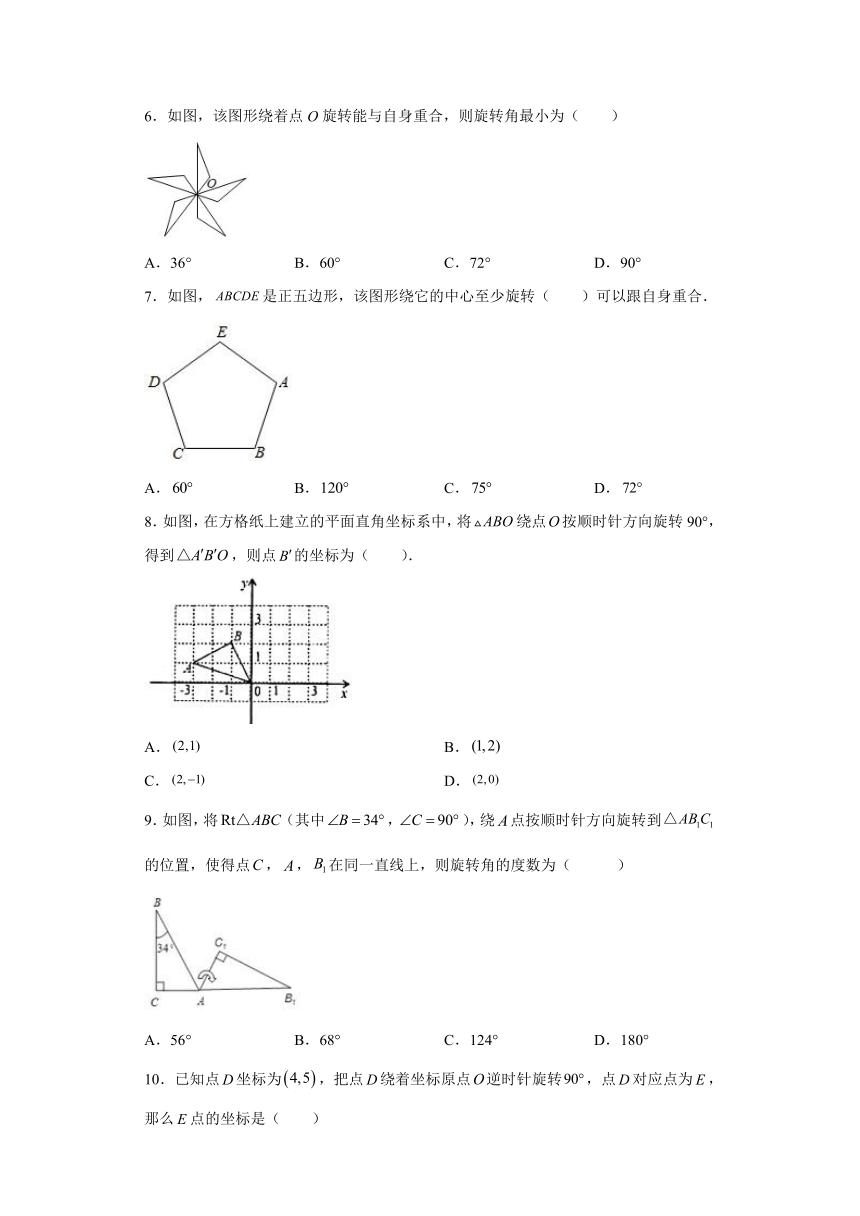


文档简介
23.1旋转作图
一、选择题
1.下列图形中,是旋转对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
2.下列图形中,不是旋转对称图形的是(
)
A.正三角形
B.等腰梯形
C.正五边形
D.正六边形
3.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转后,能与原图形完全重合的是(
)
A.
B.
C.
D.
4.如图,经过旋转或轴对称得到,其中绕点A逆时针旋转的是(
)
A.
B.
C.
D.
5.将如图所示的图形按逆时针方向旋转90 后得到图形是(
)
A.
B.
C.
D.
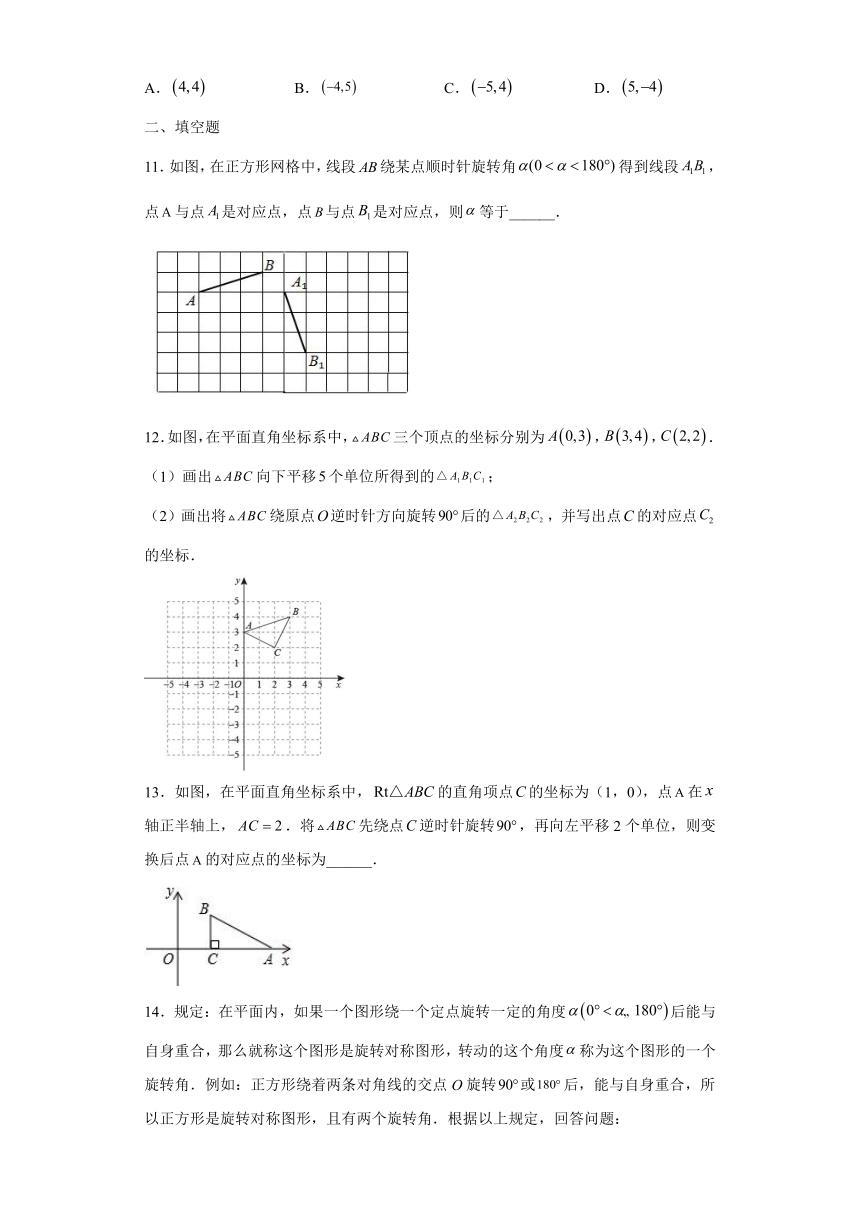
6.如图,该图形绕着点O旋转能与自身重合,则旋转角最小为( )
A.36°
B.60°
C.72°
D.90°
7.如图,是正五边形,该图形绕它的中心至少旋转(
)可以跟自身重合.
A.
B.
C.
D.
8.如图,在方格纸上建立的平面直角坐标系中,将绕点按顺时针方向旋转90°,得到,则点的坐标为(
).
A.
B.
C.
D.
9.如图,将(其中,),绕点按顺时针方向旋转到的位置,使得点,,在同一直线上,则旋转角的度数为( )
A.56°
B.68°
C.124°
D.180°
10.已知点坐标为,把点绕着坐标原点逆时针旋转,点对应点为,那么点的坐标是(
)
A.
B.
C.
D.
二、填空题
11.如图,在正方形网格中,线段绕某点顺时针旋转角得到线段,点与点是对应点,点与点是对应点,则等于______.
12.如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)画出向下平移个单位所得到的;
(2)画出将绕原点逆时针方向旋转后的,并写出点的对应点的坐标.
13.如图,在平面直角坐标系中,的直角项点的坐标为(1,0),点在轴正半轴上,.将先绕点逆时针旋转,再向左平移2个单位,则变换后点的对应点的坐标为______.
14.规定:在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转或后,能与自身重合,所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形;B.正五边形;C.菱形;D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:___________(填序号);
(3)下列三个命题:
①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形.其中真命题的个数有______个;
三、解答题
15.如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(﹣3,2),B(﹣1,4),C(0,2).
(1)将△ABC以顶点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)平移△ABC,若A的对应点A2的坐标为(5,﹣2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C1,请直接写出旋转中心的坐标.
试卷第4页,总4页
参考答案
1.C
【分析】
根据旋转对称图形的定义对四个图形进行分析即可.
【详解】
解:左边数第一个旋转180°后与初始位置重合,是旋转对称图形;
左边数第二个旋转72°后与初始位置重合,是旋转对称图形;
左边数第三个旋转120°后与初始位置重合,是旋转对称图形;
左边数第四个不是旋转对称图形.
故选:C.
【点睛】
本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
2.B
【分析】
根据旋转对称图形的定义选出正确选项.
【详解】
A选项,正三角形旋转会重合,是旋转对称图形;
B选项,不是旋转对称图形;
C选项,正五边形旋转会重合,是旋转对称图形;
D选项,正六边形旋转会重合,是旋转对称图形.
故选:B.
【点睛】
本题考查旋转对称图形,解题的关键是掌握旋转对称图形的定义.
3.D
【分析】
观察图形,从图形的性质可以确定旋转角,然后进行判断即可得到答案.
【详解】
解:A图形顺时针旋转120°后,能与原图形完全重合,A不正确;
B图形顺时针旋转90°后,能与原图形完全重合,B不正确;
C图形顺时针旋转180°后,能与原图形完全重合,C不正确;
D图形顺时针旋转72°后,能与原图形完全重合,D正确;
故选:D.
【点睛】
此题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转角度叫做旋转角.
4.D
【分析】
根据旋转的性质及轴对称的性质逐一判断即可得答案.
【详解】
A.从△ABC到△A′B′C′是绕点A逆时针旋转90°,故该选项不符合题意,
B.从△ABC到△A′B′C′是轴对称所得,故该选项不符合题意,
C.从△ABC到△A′B′C′是轴对称所得,故该选项不符合题意,
D.从△ABC到△A′B′C′是绕点A逆时针旋转60°,故该选项符合题意,
故选:D.
【点睛】
本题考查旋转的性质及轴对称的性质,正确找出对应边和对应角是解题关键.
5.A
【分析】
根据旋转的定义,观察图形即可解答.
【详解】
根据旋转的定义,图片按逆时针方向旋转90°,箭头竖直向下,从而可确定为A图.
故选A.
【点睛】
本题主要考查了旋转的性质,熟知性质是解题的关键.
6.C
【分析】
根据旋转对称图形的性质判断即可.
【详解】
解:由题意,=72°,
故该图形围绕点O旋转能与自身重合,则旋转角最小为72°,
故选:C.
【点睛】
本题考查了旋转的性质,掌握旋转的性质是解题的关键.
7.D
【分析】
根据正五边形的每个中心角相等且其和为360°即可得到结论.
【详解】
根据正五边形的性质,每个中心角的相等,则每个中心角的度数为360°÷5=72°,故该图形绕它的中心至少旋转72度可以跟自身重合.
故选:D.
【点睛】
本题考查了图形的旋转及正多边形的性质,关键是抓住正多边形的中心角相等这一性质,问题即解决.
8.A
【分析】
根据网格结构作出旋转后的图形,然后根据平面直角坐标系写出点B′的坐标即可.
【详解】
△A′B′O如图所示,点B′(2,1).
故选A.
【点睛】
本题考查了坐标与图形变化,熟练掌握网格结构,作出图形是解题的关键.
9.C
【分析】
根据旋转的定义知∠BAB1即为旋转角,则在中求解出∠BAC即可.
【详解】
在中,∠BAC=90°-34°=56°,
∴∠BAB1=180°-56°=124°,即旋转角为124°,
故选:C.
【点睛】
本题考查旋转角的确定,理解旋转角的概念是解题关键.
10.C
【分析】
建立平面直角坐标系,作出图形,然后根据图形写出点E的坐标即可.
【详解】
解:如图所示,建立平面直角坐标系,点E的坐标为( 5,4).
故选:C.
【点睛】
此题主要考查了坐标与图形变换 旋转,要熟练掌握,解答此题的关键是要明确:旋转变换只改变图形的位置,不改变图形的形状与大小.
11.90°
【分析】
连接BB1、AA1,再分别作两线段的中垂线,两中垂线的交点得出旋转中心,连接AO、A1O,结合网格特点可得旋转角;
【详解】
解:如图所示,点O为旋转中心,∠AOA1=α=90°.
故答案为:90°
【点睛】
本题主要考查作图-旋转变换,解题的关键是掌握旋转变换的定义和性质.
12.(1)见解析;(2)见解析,点的坐标为
【分析】
(1)利用平移的坐标特征写出
A1
、
B1
、
C1
的坐标,然后描点即可;
(2)利用网格特点和旋转的性质画出
A
、
B
、
C
的对应点
A2
、
B2
、
C2
并写出坐标即可;
【详解】
解(1)如图,为所作.
(2)如图,为所作.
点的对应点的坐标为,
【点睛】
本题考查了作图
旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
13.
【分析】
求出两次变换后点A的对应点的坐标即可.
【详解】
解:∵点(1,0),,
∴将△ABC先绕点C逆时针旋转90°,点A的对应点的坐标为(1,2),
∴再向左平移2个单位,变换后点A的对应点的坐标为,
故答案为:.
【点睛】
本题考查旋转变换,平移变换,解题的关键是熟练掌握基本知识,属于中考常考题型.
14.B
(1)(3)(5)
2
【分析】
(1)根据旋转对称图形的定义即可解答;
(2)分别求出各图形的旋转角即可解答;
(3)根据旋转对称图形的定义判断即可.
【详解】
(1)是旋转图形,不是中心对称图形是正五边形,故选B.
(2)图形(1)的旋转角为60°,120°,180°;图形(2)的旋转角为180°;图形(3)的旋转角为60°,120°,180°;图形(4)的旋转角为180°;图形(5)的旋转角为60°,120°,180°;图形(6)的旋转角为°,°,°,°,°;综上,是旋转对称图形,且有一个旋转角是60°的图形是.
故答案为:.
(3)根据旋转对称图形的定义可得:①中心对称图形是旋转对称图形是真命题;②等腰三角形是旋转对称图形是假命题;③圆是旋转对称图形是真命题.所以真命题有2个.
故答案为:2.
【点睛】
本题是新定义题目,熟练运用旋转对称图形的定义是解决问题的关键.
15.(1)见解析;(2)见解析;(3)图形见解析,旋转中心的坐标为(-1,0)
【分析】
(1)根据网格结构找出点A、B绕点C旋转180°后的对应点A1、B1的位置,然后顺次连接即可;
(2)根据网格结构找出点A、B、C平移后的位置,然后顺次连接即可;
(3)根据旋转的性质,确定出旋转中心即可.
【详解】
(1)△A1B1C如图所示;
(2)△A2B2C2如图所示;
(3)如图所示,旋转中心为(-1,0).
【点睛】
考查了利用旋转变换作图,解题关键是利用平移变换作图,熟练掌握网格结构以及旋转的性质,准确找出对应点的位置.
答案第7页,总7页
一、选择题
1.下列图形中,是旋转对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
2.下列图形中,不是旋转对称图形的是(
)
A.正三角形
B.等腰梯形
C.正五边形
D.正六边形
3.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转后,能与原图形完全重合的是(
)
A.
B.
C.
D.
4.如图,经过旋转或轴对称得到,其中绕点A逆时针旋转的是(
)
A.
B.
C.
D.
5.将如图所示的图形按逆时针方向旋转90 后得到图形是(
)
A.
B.
C.
D.
6.如图,该图形绕着点O旋转能与自身重合,则旋转角最小为( )
A.36°
B.60°
C.72°
D.90°
7.如图,是正五边形,该图形绕它的中心至少旋转(
)可以跟自身重合.
A.
B.
C.
D.
8.如图,在方格纸上建立的平面直角坐标系中,将绕点按顺时针方向旋转90°,得到,则点的坐标为(
).
A.
B.
C.
D.
9.如图,将(其中,),绕点按顺时针方向旋转到的位置,使得点,,在同一直线上,则旋转角的度数为( )
A.56°
B.68°
C.124°
D.180°
10.已知点坐标为,把点绕着坐标原点逆时针旋转,点对应点为,那么点的坐标是(
)
A.
B.
C.
D.
二、填空题
11.如图,在正方形网格中,线段绕某点顺时针旋转角得到线段,点与点是对应点,点与点是对应点,则等于______.
12.如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)画出向下平移个单位所得到的;
(2)画出将绕原点逆时针方向旋转后的,并写出点的对应点的坐标.
13.如图,在平面直角坐标系中,的直角项点的坐标为(1,0),点在轴正半轴上,.将先绕点逆时针旋转,再向左平移2个单位,则变换后点的对应点的坐标为______.
14.规定:在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转或后,能与自身重合,所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形;B.正五边形;C.菱形;D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:___________(填序号);
(3)下列三个命题:
①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形.其中真命题的个数有______个;
三、解答题
15.如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(﹣3,2),B(﹣1,4),C(0,2).
(1)将△ABC以顶点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)平移△ABC,若A的对应点A2的坐标为(5,﹣2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C1,请直接写出旋转中心的坐标.
试卷第4页,总4页
参考答案
1.C
【分析】
根据旋转对称图形的定义对四个图形进行分析即可.
【详解】
解:左边数第一个旋转180°后与初始位置重合,是旋转对称图形;
左边数第二个旋转72°后与初始位置重合,是旋转对称图形;
左边数第三个旋转120°后与初始位置重合,是旋转对称图形;
左边数第四个不是旋转对称图形.
故选:C.
【点睛】
本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
2.B
【分析】
根据旋转对称图形的定义选出正确选项.
【详解】
A选项,正三角形旋转会重合,是旋转对称图形;
B选项,不是旋转对称图形;
C选项,正五边形旋转会重合,是旋转对称图形;
D选项,正六边形旋转会重合,是旋转对称图形.
故选:B.
【点睛】
本题考查旋转对称图形,解题的关键是掌握旋转对称图形的定义.
3.D
【分析】
观察图形,从图形的性质可以确定旋转角,然后进行判断即可得到答案.
【详解】
解:A图形顺时针旋转120°后,能与原图形完全重合,A不正确;
B图形顺时针旋转90°后,能与原图形完全重合,B不正确;
C图形顺时针旋转180°后,能与原图形完全重合,C不正确;
D图形顺时针旋转72°后,能与原图形完全重合,D正确;
故选:D.
【点睛】
此题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转角度叫做旋转角.
4.D
【分析】
根据旋转的性质及轴对称的性质逐一判断即可得答案.
【详解】
A.从△ABC到△A′B′C′是绕点A逆时针旋转90°,故该选项不符合题意,
B.从△ABC到△A′B′C′是轴对称所得,故该选项不符合题意,
C.从△ABC到△A′B′C′是轴对称所得,故该选项不符合题意,
D.从△ABC到△A′B′C′是绕点A逆时针旋转60°,故该选项符合题意,
故选:D.
【点睛】
本题考查旋转的性质及轴对称的性质,正确找出对应边和对应角是解题关键.
5.A
【分析】
根据旋转的定义,观察图形即可解答.
【详解】
根据旋转的定义,图片按逆时针方向旋转90°,箭头竖直向下,从而可确定为A图.
故选A.
【点睛】
本题主要考查了旋转的性质,熟知性质是解题的关键.
6.C
【分析】
根据旋转对称图形的性质判断即可.
【详解】
解:由题意,=72°,
故该图形围绕点O旋转能与自身重合,则旋转角最小为72°,
故选:C.
【点睛】
本题考查了旋转的性质,掌握旋转的性质是解题的关键.
7.D
【分析】
根据正五边形的每个中心角相等且其和为360°即可得到结论.
【详解】
根据正五边形的性质,每个中心角的相等,则每个中心角的度数为360°÷5=72°,故该图形绕它的中心至少旋转72度可以跟自身重合.
故选:D.
【点睛】
本题考查了图形的旋转及正多边形的性质,关键是抓住正多边形的中心角相等这一性质,问题即解决.
8.A
【分析】
根据网格结构作出旋转后的图形,然后根据平面直角坐标系写出点B′的坐标即可.
【详解】
△A′B′O如图所示,点B′(2,1).
故选A.
【点睛】
本题考查了坐标与图形变化,熟练掌握网格结构,作出图形是解题的关键.
9.C
【分析】
根据旋转的定义知∠BAB1即为旋转角,则在中求解出∠BAC即可.
【详解】
在中,∠BAC=90°-34°=56°,
∴∠BAB1=180°-56°=124°,即旋转角为124°,
故选:C.
【点睛】
本题考查旋转角的确定,理解旋转角的概念是解题关键.
10.C
【分析】
建立平面直角坐标系,作出图形,然后根据图形写出点E的坐标即可.
【详解】
解:如图所示,建立平面直角坐标系,点E的坐标为( 5,4).
故选:C.
【点睛】
此题主要考查了坐标与图形变换 旋转,要熟练掌握,解答此题的关键是要明确:旋转变换只改变图形的位置,不改变图形的形状与大小.
11.90°
【分析】
连接BB1、AA1,再分别作两线段的中垂线,两中垂线的交点得出旋转中心,连接AO、A1O,结合网格特点可得旋转角;
【详解】
解:如图所示,点O为旋转中心,∠AOA1=α=90°.
故答案为:90°
【点睛】
本题主要考查作图-旋转变换,解题的关键是掌握旋转变换的定义和性质.
12.(1)见解析;(2)见解析,点的坐标为
【分析】
(1)利用平移的坐标特征写出
A1
、
B1
、
C1
的坐标,然后描点即可;
(2)利用网格特点和旋转的性质画出
A
、
B
、
C
的对应点
A2
、
B2
、
C2
并写出坐标即可;
【详解】
解(1)如图,为所作.
(2)如图,为所作.
点的对应点的坐标为,
【点睛】
本题考查了作图
旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
13.
【分析】
求出两次变换后点A的对应点的坐标即可.
【详解】
解:∵点(1,0),,
∴将△ABC先绕点C逆时针旋转90°,点A的对应点的坐标为(1,2),
∴再向左平移2个单位,变换后点A的对应点的坐标为,
故答案为:.
【点睛】
本题考查旋转变换,平移变换,解题的关键是熟练掌握基本知识,属于中考常考题型.
14.B
(1)(3)(5)
2
【分析】
(1)根据旋转对称图形的定义即可解答;
(2)分别求出各图形的旋转角即可解答;
(3)根据旋转对称图形的定义判断即可.
【详解】
(1)是旋转图形,不是中心对称图形是正五边形,故选B.
(2)图形(1)的旋转角为60°,120°,180°;图形(2)的旋转角为180°;图形(3)的旋转角为60°,120°,180°;图形(4)的旋转角为180°;图形(5)的旋转角为60°,120°,180°;图形(6)的旋转角为°,°,°,°,°;综上,是旋转对称图形,且有一个旋转角是60°的图形是.
故答案为:.
(3)根据旋转对称图形的定义可得:①中心对称图形是旋转对称图形是真命题;②等腰三角形是旋转对称图形是假命题;③圆是旋转对称图形是真命题.所以真命题有2个.
故答案为:2.
【点睛】
本题是新定义题目,熟练运用旋转对称图形的定义是解决问题的关键.
15.(1)见解析;(2)见解析;(3)图形见解析,旋转中心的坐标为(-1,0)
【分析】
(1)根据网格结构找出点A、B绕点C旋转180°后的对应点A1、B1的位置,然后顺次连接即可;
(2)根据网格结构找出点A、B、C平移后的位置,然后顺次连接即可;
(3)根据旋转的性质,确定出旋转中心即可.
【详解】
(1)△A1B1C如图所示;
(2)△A2B2C2如图所示;
(3)如图所示,旋转中心为(-1,0).
【点睛】
考查了利用旋转变换作图,解题关键是利用平移变换作图,熟练掌握网格结构以及旋转的性质,准确找出对应点的位置.
答案第7页,总7页
同课章节目录
