2020-2021学年山东省烟台市海阳市八年级(下)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省烟台市海阳市八年级(下)期末数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览




文档简介
2020-2021学年山东省烟台市海阳市八年级(下)期末数学试卷(五四学制)
一、选择题(共12个小题,每小题3分,满分36分).
1.下列二次根式中,与是同类二次根式的是( )
A.
B.
C.
D.
2.下列等式正确的是( )
A.5=
B.=
C.=﹣
D.=1
3.下列方程中,没有实数根的是方程( )
A.﹣3x2+2x+10=0
B.2x2+8x﹣3=0
C.3x2+2x=1
D.x2+3x+3=0
4.根据下列表格的对应值:
x
﹣1
1
1.1
1.2
x2+12x﹣15
﹣26
﹣2
﹣0.59
0.84
由此可判断方程x2+12x﹣15=0必有一个解x满足( )
A.﹣1<x<1
B.1<x<1.1
C.1.1<x<1.2
D.﹣0.59<x<0.84
5.用配方法解方程3x2+2x﹣1=0,配方后的方程是( )
A.3(x﹣1)2=0
B.(x+)2=
C.(x+)2=
D.(x+)2=
6.若关于x的方程kx2+2x+1=0有实数根,则实数k的取值范围是( )
A.k≠0
B.k≤1
C.k≥1
D.k≤1且k≠0
7.如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A.BA=BC
B.AC、BD互相平分
C.AC=BD
D.AB∥CD
8.在菱形ABCD中,对角线BD=4,∠ABC=120°,则菱形ABCD的面积为( )
A.16
B.4
C.8
D.16
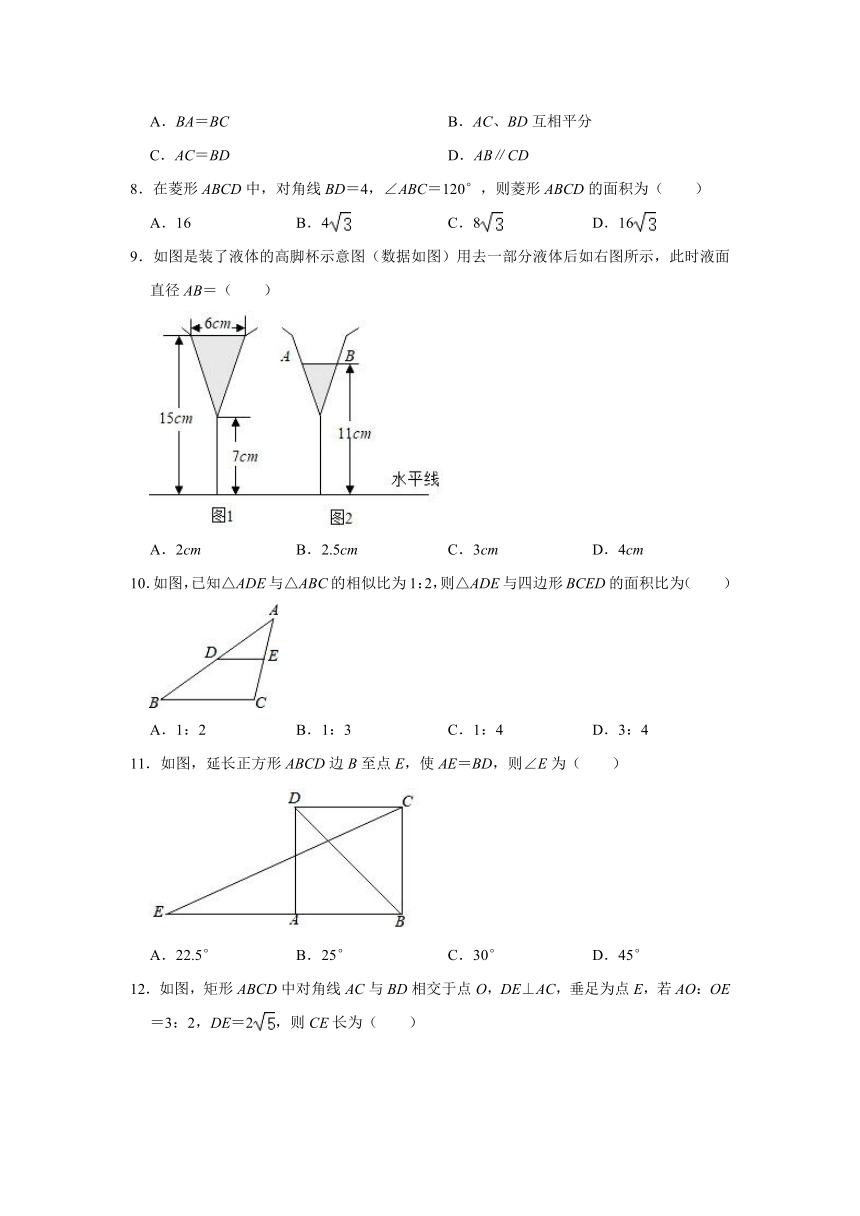
9.如图是装了液体的高脚杯示意图(数据如图)用去一部分液体后如右图所示,此时液面直径AB=( )
A.2cm
B.2.5cm
C.3cm
D.4cm
10.如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )
A.1:2
B.1:3
C.1:4
D.3:4
11.如图,延长正方形ABCD边B至点E,使AE=BD,则∠E为( )
A.22.5°
B.25°
C.30°
D.45°
12.如图,矩形ABCD中对角线AC与BD相交于点O,DE⊥AC,垂足为点E,若AO:OE=3:2,DE=2,则CE长为( )
A.1
B.2
C.
D.
二、填空题:(本大题共6个小题,每小题3分,满分18分)
13.若使在实数范围内有意义,则x的取值范围为
.
14.计算3 ÷=
.
15.已知==(b+d≠0),则的值为
.
16.如图,在平面直角坐标系中,△ABO的顶点都在坐标轴上,OA=4.若△CDO是以原点O为位似图形,△ABO的位似图形(C为点A的对应点),且△CDO与△ABO相似比为,则点C的坐标为
.
17.若x=2﹣是方程x2﹣4x+c=0的一个根,则c的值是
.
18.如图,在Rt△ABC纸板中,AC=4,BC=3,P是AC上一点,过点P沿直线剪一次剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是
.
三、解答题(本大题共7个小题,满分66分)
19.解下列方程:
(1)(x﹣)2=;
(2)x(x﹣2)=(x﹣2);
20.已知:如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,DE∥AC,CE∥AD,连接BE,CD.求证:四边形CDBE是正方形.
21.如图,已知在△ABC和△DAC中,∠B=∠DAC,∠D=115°,E,F分别为AB和BC上的点,且EF∥AC,AE=AD,CF=AC.
(1)求∠BAC的度数;
(2)若BC=8,CD=,求的值.
22.李先生存入银行4万元,先存一个一年定期,一年后将本息自动转存为一个一年定期,年利率不变,两年后共得本息4.1412万元.
(1)一年定期存款的年利率为多少?(参考数值:=2.035)
(2)若两年定期存款的年利率为2.25%,则李先生4万元存款已得到的利息比按两年定期存款所得利息少多少元?
23.如图,在边长为8的正方形ABCD中,点M是边DC上一动点(点M不与边DC端
点重合),点O在边AD上,且OA=OM,作MN⊥MO,交BC于点N.设DM=x,OM=y.
(1)求证:△OMD∽△MNC.
(2)求y关于x的函数表达式.
(3)当x=2时,求△MNC的周长.
24.如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)是否存在某时刻t使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由;
(2)如果BP=PQ,求此时t的值.
25.如图,在△ABC中,∠C=90°,AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,过点A作AE⊥AD交BD的延长线于点E,△ABC∽△EDA.
(1)求∠ABC的度数;
(2)求的值.
参考答案
一、选择题(本大题共12个小题,每小题3分,满分36分).下列每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的
1.下列二次根式中,与是同类二次根式的是( )
A.
B.
C.
D.
【分析】把各项进行化简,再根据同类二次根式的概念逐一判断即可.
解:A.∵,被开方数不相同,
∴不是同类二次根式,故本选项不符合题意;
B.∵,被开方数不相同,
∴不是同类二次根式,故本选项不符合题意;
C.∵,被开方数相同,
∴是同类二次根式,故本选项符合题意;
D.∵,被开方数不相同,
∴不是同类二次根式,故本选项不符合题意;
故选:C.
2.下列等式正确的是( )
A.5=
B.=
C.=﹣
D.=1
【分析】利用二次根式的乘除法法则,以及二次根式的化简对各项进行运算,即可求解.
解:A、,故A符合题意;
B、,故B不符合题意;
C、,故C不符合题意;
D、,故D不符合题意.
故选:A.
3.下列方程中,没有实数根的是方程( )
A.﹣3x2+2x+10=0
B.2x2+8x﹣3=0
C.3x2+2x=1
D.x2+3x+3=0
【分析】分别计算四个方程的判别式的值,然后根据判别式的意义进行判断.
解:A、Δ=b2﹣4ac=22﹣4×(﹣3)×10=124>0,方程有两个不相等的实数根,所以A选项错误;
B、Δ=b2﹣4ac=82﹣4×2×(﹣3)=88>0,方程有两个不相等的实数根,所以B选项错误;
C、Δ=b2﹣4ac=22﹣4×3×(﹣1)=16>0,方程有两个不相等的实数根,所以C选项错误;
D、Δ=b2﹣4ac=32﹣4×1×3=﹣3<0,方程没有实数根,所以D选项正确.
故选:D.
4.根据下列表格的对应值:
x
﹣1
1
1.1
1.2
x2+12x﹣15
﹣26
﹣2
﹣0.59
0.84
由此可判断方程x2+12x﹣15=0必有一个解x满足( )
A.﹣1<x<1
B.1<x<1.1
C.1.1<x<1.2
D.﹣0.59<x<0.84
【分析】利用表中数据得到x=1.1时,x2+12x﹣15=﹣0.59<0,x=1.2时,x2+12x﹣15=0.84>0,则可判断x2+12x﹣15=0时,1.1<x<1.2.
解:∵x=1.1时,x2+12x﹣15=﹣0.59<0,
x=1.2时,x2+12x﹣15=0.84>0,
∴x2+12x﹣15=0时,1.1<x<1.2,
即方程x2+12x﹣15=0必有一个解x满足1.1<x<1.2,
故选:C.
5.用配方法解方程3x2+2x﹣1=0,配方后的方程是( )
A.3(x﹣1)2=0
B.(x+)2=
C.(x+)2=
D.(x+)2=
【分析】方程整理后,利用完全平方公式配方可得到结果.
解:方程3x2+2x﹣1=0,
变形得:x2+x=,
配方得:x2+x+=,即(x+)2=,
故选:D.
6.若关于x的方程kx2+2x+1=0有实数根,则实数k的取值范围是( )
A.k≠0
B.k≤1
C.k≥1
D.k≤1且k≠0
【分析】根据一元二次方程的根的判别式即可求出答案.
解:当k≠0时,Δ=4﹣4k≥0,
∴k≤1,即k≤1且k≠0,
当k=0时,
此时方程为2x+1=0,满足题意,
∴k≤1.
故选:B.
7.如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A.BA=BC
B.AC、BD互相平分
C.AC=BD
D.AB∥CD
【分析】已知四边形的对角线互相垂直,可依据“对角线互相垂直且平分的四边形是菱形”的判定方法,来选择条件.
解:四边形ABCD中,AC、BD互相垂直,
若四边形ABCD是菱形,需添加的条件是:
AC、BD互相平分;(对角线互相垂直且平分的四边形是菱形)
故选:B.
8.在菱形ABCD中,对角线BD=4,∠ABC=120°,则菱形ABCD的面积为( )
A.16
B.4
C.8
D.16
【分析】作出图形,连接AC、BD,根据菱形的对角线互相垂直平分可得AC⊥BD,OB=BD,菱形的对角线平分一组对角求出∠ABO=60°,再求出AB,AC,进而解答即可.
解:如图,连接AC、BD,
在菱形ABCD中,AC⊥BD,OB=BD=×4=2,
∵∠BAD=120°,
∴∠BAO=60°,
在Rt△AOB中,AB=2OB=4,OA=OB=2,
∴AC=2OA=4,
∴菱形ABCD的面积=,
故选:C.
9.如图是装了液体的高脚杯示意图(数据如图)用去一部分液体后如右图所示,此时液面直径AB=( )
A.2cm
B.2.5cm
C.3cm
D.4cm
【分析】高脚杯前后的两个三角形相似,根据相似三角形的判定和性质即可得出结果.
解:如图:过O作OM⊥CD,垂足为M,过O′作O′N⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO′,即相似比为,
∴=,
∵OM=15﹣7=8(cm),O′N=11﹣7=4(cm),
∴=
∴AB=3(cm),
故选:C.
10.如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )
A.1:2
B.1:3
C.1:4
D.3:4
【分析】由三角形ADE与三角形ABC相似,利用相似三角形面积之比等于相似比,求出两三角形面积之比,即可求出△ADE与四边形BCED的面积比.
解:∵△ADE∽△ABC,且相似比为1:2,
∴S△ADE:S△ABC=1:4,
∵S△ABC=S四边形BCED+S△ADE,
∴S△ADE:S四边形BCED=1:3,
故选:B.
11.如图,延长正方形ABCD边B至点E,使AE=BD,则∠E为( )
A.22.5°
B.25°
C.30°
D.45°
【分析】连接AC,根据题意可得AC=BD=CE,则∠ACE=∠E,由外角的性质可得:∠CAB=∠ACE+∠E=45°,即可求解.
解:连接AC,
∵四边形ABCD是正方形,
∴AC=BD,且∠CAB=45°,
又∵BD=AE,
∴AE=CA,
∴∠E=∠ACE,
∵∠CAB=∠ACE+∠E=2∠E=45°,
∴∠E=22.5°.
故选:A.
12.如图,矩形ABCD中对角线AC与BD相交于点O,DE⊥AC,垂足为点E,若AO:OE=3:2,DE=2,则CE长为( )
A.1
B.2
C.
D.
【分析】由矩形的性质得到∠ADC=90°,BD=AC,OD=BD,OC=AC,求得OC=OD,设OA=3x,OE=2x,得到OD=OA=3x,根据勾股定理即可得到结论.
解:∵四边形ABCD是矩形,
∴AC=BD,OD=BD,OC=AC,∠ADC=90°,
∴OC=OD,
∵AO:OE=3:2,DE⊥AC,
设OA=3x,OE=2x,
在Rt△DOE中,OD2=OE2+DE2,
即,
解得:x=2或x=﹣2(舍去),
∴OC=OA=6,OE=4,
∴EC=OC﹣OE=6﹣4=2,
故选:B.
二、填空题:(本大题共6个小题,每小题3分,满分18分)
13.若使在实数范围内有意义,则x的取值范围为
x<2 .
【分析】根据二次根式有意义时被开方数为非负数,分式的分母不为零列式计算可求解.
解:由题意得6﹣3x>0,
解得x<2,
故答案为x<2.
14.计算3 ÷= .
【分析】利用二次根式乘除法的法则对式子进行运算即可求解.
解:3 ÷
=3÷
=
=.
故答案为:.
15.已知==(b+d≠0),则的值为
.
【分析】根据合比的性质即可求解.
解:∵==(b+d≠0),
∴=.
故答案为:.
16.如图,在平面直角坐标系中,△ABO的顶点都在坐标轴上,OA=4.若△CDO是以原点O为位似图形,△ABO的位似图形(C为点A的对应点),且△CDO与△ABO相似比为,则点C的坐标为
(2,0)或(﹣2,0) .
【分析】先写出A点坐标,然后根据关于原点为位似中心的对应点的坐标关系,把A点的横纵坐标都乘以(或﹣)得到C点坐标.
解:∵OA=4,
∴A(4,0),
∵△CDO是以原点O为位似图形,△ABO的位似图形,且△CDO与△ABO相似比为,
∴C点坐标为(×4,0)或(﹣×4,0),即C(2,0)或(﹣2,0).
故答案为(2,0)或(﹣2,0).
17.若x=2﹣是方程x2﹣4x+c=0的一个根,则c的值是 1 .
【分析】把x=2﹣代入方程x2﹣4x+c=0就得到关于c的方程,就可以解得c的值.
解:把x=2﹣代入方程x2﹣4x+c=0,得(2﹣)2﹣4(2﹣)+c=0,
解得c=1;
故答案为:1.
18.如图,在Rt△ABC纸板中,AC=4,BC=3,P是AC上一点,过点P沿直线剪一次剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是
0<CP≤ .
【分析】分四种情况讨论,依据相似三角形的对应边成比例,即可得到CP长的取值范围.
解:如图所示,过P作PD∥AB交BC于D或PE∥BC交AB于E,则△PCD∽△ACB或△APE∽△ACB,
此时0<CP<4;
如图所示,过P作∠APF=∠B交AB于F,则△APF∽△ABC,
此时0≤CP<4;
如图所示,过P作∠CPG=∠CBA交BC于G,则△CPG∽△CBA,
当点G与点B重合时,CB2=CP×CA,即32=CP×4,
∴CP=,
∴此时,0<CP≤;
综上所述,CP长的取值范围是0<CP≤.
故答案为:0<CP≤.
三、解答题(本大题共7个小题,满分66分)
19.解下列方程:
(1)(x﹣)2=;
(2)x(x﹣2)=(x﹣2);
【分析】(1)由直接开平方法可得出答案;
(2)方程左边因式分解得到两个一元一次方程,解方程即可求出方程的解.
解:(1)原方程可变形为,
∴x1=,x2=;
(2)原方程可变形为x(x﹣2)﹣(x﹣2)=0,
∴=0,
∴x﹣2=0或x﹣=0,
∴x1=2,x2=.
20.已知:如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,DE∥AC,CE∥AD,连接BE,CD.求证:四边形CDBE是正方形.
【分析】根据平行四边形的判定和性质得出DE=AC,CE=AD,进而利用正方形的判定解答即可.
【解答】证明:∵DE∥AC,CE∥AD,
∴四边形ADEC是平行四边形,
∴DE=AC,CE=AD,
∵AD=DB,
∴CE=DB,
∵CE∥DB,
∴四边形DBEC是平行四边形,
∵AC=BC,
∴BC=DE,
∴平行四边形DBEC是矩形,
∵∠ACB=90°,
∴CD=AD=DB,
∴矩形DBEC是正方形.
21.如图,已知在△ABC和△DAC中,∠B=∠DAC,∠D=115°,E,F分别为AB和BC上的点,且EF∥AC,AE=AD,CF=AC.
(1)求∠BAC的度数;
(2)若BC=8,CD=,求的值.
【分析】(1)根据平行线分线段成比例可得,从而得出,可证△ABC∽△DAC,得出答案;
(2)由(1)相似可求出AC=6,E根据F∥AC,可得.
解:(1)∵EF∥AC,
∴,
∵AE=AD,CF=AC,
∴,
∵∠B=∠DAC,
∴△ABC∽△DAC,
∴∠BAC=∠D=115°,
(2)∵△ABC∽△DAC,
∴,
∴=36,
∵AC>0,
∴AC=6,
∴CF=6,
∵EF∥AC,
∴.
22.李先生存入银行4万元,先存一个一年定期,一年后将本息自动转存为一个一年定期,年利率不变,两年后共得本息4.1412万元.
(1)一年定期存款的年利率为多少?(参考数值:=2.035)
(2)若两年定期存款的年利率为2.25%,则李先生4万元存款已得到的利息比按两年定期存款所得利息少多少元?
【分析】(1)设一年定期存款的年利率为x,利用两年后的本息和=本金×(1+年利率)2,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)利用利息=本金×年利率×存款年数,可求出按两年定期存款获得的利润,再将两种存款方式获得的利润做差后即可得出结论.
解:(1)设一年定期存款的年利率为x,
依题意得:4(1+x)2=4.1412,
解得:x1=0.0175=1.75%,x2=﹣2.0175(不合题意,舍去).
答:一年定期存款的年利率为1.75%.
(2)40000×2.25%×2=1800(元),
1800﹣(41412﹣40000)=388(元).
答:李先生4万元存款已得到的利息比按两年定期存款所得利息少388元.
23.如图,在边长为8的正方形ABCD中,点M是边DC上一动点(点M不与边DC端
点重合),点O在边AD上,且OA=OM,作MN⊥MO,交BC于点N.设DM=x,OM=y.
(1)求证:△OMD∽△MNC.
(2)求y关于x的函数表达式.
(3)当x=2时,求△MNC的周长.
【分析】(1)由直角三角形的性质得出∠DOM=∠CMN,根据相似三角形的判定方法可得出结论;
(2)由勾股定理得出(8﹣y)2+x2=y2,则可得出答案;
(3)当x=2时,求出y=,由相似三角形的性质可得出答案.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∴∠DMO+∠DOM=90°,
又∵∠DMO+∠OMN+∠CMN=180°,∠OMN=90°,
∴∠DMO+∠CMN=90°,
∴∠DOM=∠CMN,
∴△OMD∽△MNC;
(2)在Rt△OMD中,OD=AD﹣OA=8﹣y,
由勾股定理得,(8﹣y)2+x2=y2,
∴y=;
(3)当x=2时,y=,
∵OA=OM,
∴△OMD的周长=AD+DM=x+8=2+8=10,OD=8﹣y=8﹣=,
∵△MNC∽△OMD,
∴△MNC的周长:△OMD的周长=MC:OD,
即△MNC的周长:10=(8﹣2):,
∴△MNC的周长=16.
24.如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)是否存在某时刻t使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由;
(2)如果BP=PQ,求此时t的值.
【分析】(1)根据PD∥BC,可得=,所以=,得PD=,由S△APQ=2t×=﹣t2+6t=12,得t2﹣5t+10=0,由△=(﹣5)2﹣4×1×10=﹣15<0,可得不存在某时刻t,使线段PQ恰好把△ABC的面积平分;
(2)根据勾股定理可得QD2+PD2=PQ2,所以得()2+()2=(2t)2,解方程可得t的值.
解:(1)不存在某时刻t,使线段PQ恰好把△ABC的面积平分,理由如下:
如图,过点P作PD⊥AC于点D,
∴PD∥BC,
在Rt△ABC中,∠C=90°,
∵AB=10cm,AC=8cm.
∴BC=6cm,
假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△APQ=S△ABC,
∵S△ABC=AC BC=8×6=24(cm2),
∴S△APQ=12(cm2),
∵PD∥BC,
∴=,
∴=,
∴PD=,
∴S△APQ=2t×=﹣t2+6t,
∴﹣t2+6t=12,
化简得t2﹣5t+10=0,
∵△=(﹣5)2﹣4×1×10=﹣15<0,
∴此方程无实数根,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分;
(2)∵PD∥BC,
∴=,
∴=,
∴AD=,
∵PD=,PQ=BP=2t,
∴QD=AD﹣AQ=﹣2t=,
在Rt△PQD中,根据勾股定理,得
QD2+PD2=PQ2,
∴()2+()2=(2t)2,
化简,得13t2﹣90t+125=0,
解得t1=5,t2=,
∵t=5>4,不符合题意,舍去,
∴t=s.
25.如图,在△ABC中,∠C=90°,AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,过点A作AE⊥AD交BD的延长线于点E,△ABC∽△EDA.
(1)求∠ABC的度数;
(2)求的值.
【分析】(1)依据三角形内角和定理以及角平分线的定义,即可得到∠1+∠2的度数,根据三角形外角性质即可得出∠3的度数,最后根据相似三角形的对应角相等,即可得出结论;
(2)过A作AF⊥DE于点F,设AF=a,易得DE=2a,DF=a,AD=a,BF=a+a,依据勾股定理即可得到AB2=AF2+BF2=(4+2)a2,最后根据相似三角形的面积的比等于相似比的平方,即可得出结论.
解:(1)∵AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,
∴∠1=∠ABC,∠2=∠BAC,
∵∠C=90°,
∴∠1+∠2=(∠ABC+∠BAC)=90°=45°,
∴∠3=∠1+∠2=45°,
∵△ABC∽△EDA,
∴∠ABC=∠3=45°;
(2)过A作AF⊥DE于点F,
∵∠3=45°,AE⊥AD,
∴△ADE是等腰直角三角形,
设AF=a,则DE=2a,DF=a,
Rt△ADF中,AD=a,
∵2∠1=2∠2=45°,
∴∠1=∠2,
∴AD=BD=a,
∴BF=a+a,
在Rt△ABF中,AB2=AF2+BF2=a2+(a+a)2=(4+2)a2,
∵△ABC∽△EDA,
∴===.
一、选择题(共12个小题,每小题3分,满分36分).
1.下列二次根式中,与是同类二次根式的是( )
A.
B.
C.
D.
2.下列等式正确的是( )
A.5=
B.=
C.=﹣
D.=1
3.下列方程中,没有实数根的是方程( )
A.﹣3x2+2x+10=0
B.2x2+8x﹣3=0
C.3x2+2x=1
D.x2+3x+3=0
4.根据下列表格的对应值:
x
﹣1
1
1.1
1.2
x2+12x﹣15
﹣26
﹣2
﹣0.59
0.84
由此可判断方程x2+12x﹣15=0必有一个解x满足( )
A.﹣1<x<1
B.1<x<1.1
C.1.1<x<1.2
D.﹣0.59<x<0.84
5.用配方法解方程3x2+2x﹣1=0,配方后的方程是( )
A.3(x﹣1)2=0
B.(x+)2=
C.(x+)2=
D.(x+)2=
6.若关于x的方程kx2+2x+1=0有实数根,则实数k的取值范围是( )
A.k≠0
B.k≤1
C.k≥1
D.k≤1且k≠0
7.如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A.BA=BC
B.AC、BD互相平分
C.AC=BD
D.AB∥CD
8.在菱形ABCD中,对角线BD=4,∠ABC=120°,则菱形ABCD的面积为( )
A.16
B.4
C.8
D.16
9.如图是装了液体的高脚杯示意图(数据如图)用去一部分液体后如右图所示,此时液面直径AB=( )
A.2cm
B.2.5cm
C.3cm
D.4cm
10.如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )
A.1:2
B.1:3
C.1:4
D.3:4
11.如图,延长正方形ABCD边B至点E,使AE=BD,则∠E为( )
A.22.5°
B.25°
C.30°
D.45°
12.如图,矩形ABCD中对角线AC与BD相交于点O,DE⊥AC,垂足为点E,若AO:OE=3:2,DE=2,则CE长为( )
A.1
B.2
C.
D.
二、填空题:(本大题共6个小题,每小题3分,满分18分)
13.若使在实数范围内有意义,则x的取值范围为
.
14.计算3 ÷=
.
15.已知==(b+d≠0),则的值为
.
16.如图,在平面直角坐标系中,△ABO的顶点都在坐标轴上,OA=4.若△CDO是以原点O为位似图形,△ABO的位似图形(C为点A的对应点),且△CDO与△ABO相似比为,则点C的坐标为
.
17.若x=2﹣是方程x2﹣4x+c=0的一个根,则c的值是
.
18.如图,在Rt△ABC纸板中,AC=4,BC=3,P是AC上一点,过点P沿直线剪一次剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是
.
三、解答题(本大题共7个小题,满分66分)
19.解下列方程:
(1)(x﹣)2=;
(2)x(x﹣2)=(x﹣2);
20.已知:如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,DE∥AC,CE∥AD,连接BE,CD.求证:四边形CDBE是正方形.
21.如图,已知在△ABC和△DAC中,∠B=∠DAC,∠D=115°,E,F分别为AB和BC上的点,且EF∥AC,AE=AD,CF=AC.
(1)求∠BAC的度数;
(2)若BC=8,CD=,求的值.
22.李先生存入银行4万元,先存一个一年定期,一年后将本息自动转存为一个一年定期,年利率不变,两年后共得本息4.1412万元.
(1)一年定期存款的年利率为多少?(参考数值:=2.035)
(2)若两年定期存款的年利率为2.25%,则李先生4万元存款已得到的利息比按两年定期存款所得利息少多少元?
23.如图,在边长为8的正方形ABCD中,点M是边DC上一动点(点M不与边DC端
点重合),点O在边AD上,且OA=OM,作MN⊥MO,交BC于点N.设DM=x,OM=y.
(1)求证:△OMD∽△MNC.
(2)求y关于x的函数表达式.
(3)当x=2时,求△MNC的周长.
24.如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)是否存在某时刻t使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由;
(2)如果BP=PQ,求此时t的值.
25.如图,在△ABC中,∠C=90°,AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,过点A作AE⊥AD交BD的延长线于点E,△ABC∽△EDA.
(1)求∠ABC的度数;
(2)求的值.
参考答案
一、选择题(本大题共12个小题,每小题3分,满分36分).下列每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的
1.下列二次根式中,与是同类二次根式的是( )
A.
B.
C.
D.
【分析】把各项进行化简,再根据同类二次根式的概念逐一判断即可.
解:A.∵,被开方数不相同,
∴不是同类二次根式,故本选项不符合题意;
B.∵,被开方数不相同,
∴不是同类二次根式,故本选项不符合题意;
C.∵,被开方数相同,
∴是同类二次根式,故本选项符合题意;
D.∵,被开方数不相同,
∴不是同类二次根式,故本选项不符合题意;
故选:C.
2.下列等式正确的是( )
A.5=
B.=
C.=﹣
D.=1
【分析】利用二次根式的乘除法法则,以及二次根式的化简对各项进行运算,即可求解.
解:A、,故A符合题意;
B、,故B不符合题意;
C、,故C不符合题意;
D、,故D不符合题意.
故选:A.
3.下列方程中,没有实数根的是方程( )
A.﹣3x2+2x+10=0
B.2x2+8x﹣3=0
C.3x2+2x=1
D.x2+3x+3=0
【分析】分别计算四个方程的判别式的值,然后根据判别式的意义进行判断.
解:A、Δ=b2﹣4ac=22﹣4×(﹣3)×10=124>0,方程有两个不相等的实数根,所以A选项错误;
B、Δ=b2﹣4ac=82﹣4×2×(﹣3)=88>0,方程有两个不相等的实数根,所以B选项错误;
C、Δ=b2﹣4ac=22﹣4×3×(﹣1)=16>0,方程有两个不相等的实数根,所以C选项错误;
D、Δ=b2﹣4ac=32﹣4×1×3=﹣3<0,方程没有实数根,所以D选项正确.
故选:D.
4.根据下列表格的对应值:
x
﹣1
1
1.1
1.2
x2+12x﹣15
﹣26
﹣2
﹣0.59
0.84
由此可判断方程x2+12x﹣15=0必有一个解x满足( )
A.﹣1<x<1
B.1<x<1.1
C.1.1<x<1.2
D.﹣0.59<x<0.84
【分析】利用表中数据得到x=1.1时,x2+12x﹣15=﹣0.59<0,x=1.2时,x2+12x﹣15=0.84>0,则可判断x2+12x﹣15=0时,1.1<x<1.2.
解:∵x=1.1时,x2+12x﹣15=﹣0.59<0,
x=1.2时,x2+12x﹣15=0.84>0,
∴x2+12x﹣15=0时,1.1<x<1.2,
即方程x2+12x﹣15=0必有一个解x满足1.1<x<1.2,
故选:C.
5.用配方法解方程3x2+2x﹣1=0,配方后的方程是( )
A.3(x﹣1)2=0
B.(x+)2=
C.(x+)2=
D.(x+)2=
【分析】方程整理后,利用完全平方公式配方可得到结果.
解:方程3x2+2x﹣1=0,
变形得:x2+x=,
配方得:x2+x+=,即(x+)2=,
故选:D.
6.若关于x的方程kx2+2x+1=0有实数根,则实数k的取值范围是( )
A.k≠0
B.k≤1
C.k≥1
D.k≤1且k≠0
【分析】根据一元二次方程的根的判别式即可求出答案.
解:当k≠0时,Δ=4﹣4k≥0,
∴k≤1,即k≤1且k≠0,
当k=0时,
此时方程为2x+1=0,满足题意,
∴k≤1.
故选:B.
7.如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A.BA=BC
B.AC、BD互相平分
C.AC=BD
D.AB∥CD
【分析】已知四边形的对角线互相垂直,可依据“对角线互相垂直且平分的四边形是菱形”的判定方法,来选择条件.
解:四边形ABCD中,AC、BD互相垂直,
若四边形ABCD是菱形,需添加的条件是:
AC、BD互相平分;(对角线互相垂直且平分的四边形是菱形)
故选:B.
8.在菱形ABCD中,对角线BD=4,∠ABC=120°,则菱形ABCD的面积为( )
A.16
B.4
C.8
D.16
【分析】作出图形,连接AC、BD,根据菱形的对角线互相垂直平分可得AC⊥BD,OB=BD,菱形的对角线平分一组对角求出∠ABO=60°,再求出AB,AC,进而解答即可.
解:如图,连接AC、BD,
在菱形ABCD中,AC⊥BD,OB=BD=×4=2,
∵∠BAD=120°,
∴∠BAO=60°,
在Rt△AOB中,AB=2OB=4,OA=OB=2,
∴AC=2OA=4,
∴菱形ABCD的面积=,
故选:C.
9.如图是装了液体的高脚杯示意图(数据如图)用去一部分液体后如右图所示,此时液面直径AB=( )
A.2cm
B.2.5cm
C.3cm
D.4cm
【分析】高脚杯前后的两个三角形相似,根据相似三角形的判定和性质即可得出结果.
解:如图:过O作OM⊥CD,垂足为M,过O′作O′N⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO′,即相似比为,
∴=,
∵OM=15﹣7=8(cm),O′N=11﹣7=4(cm),
∴=
∴AB=3(cm),
故选:C.
10.如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )
A.1:2
B.1:3
C.1:4
D.3:4
【分析】由三角形ADE与三角形ABC相似,利用相似三角形面积之比等于相似比,求出两三角形面积之比,即可求出△ADE与四边形BCED的面积比.
解:∵△ADE∽△ABC,且相似比为1:2,
∴S△ADE:S△ABC=1:4,
∵S△ABC=S四边形BCED+S△ADE,
∴S△ADE:S四边形BCED=1:3,
故选:B.
11.如图,延长正方形ABCD边B至点E,使AE=BD,则∠E为( )
A.22.5°
B.25°
C.30°
D.45°
【分析】连接AC,根据题意可得AC=BD=CE,则∠ACE=∠E,由外角的性质可得:∠CAB=∠ACE+∠E=45°,即可求解.
解:连接AC,
∵四边形ABCD是正方形,
∴AC=BD,且∠CAB=45°,
又∵BD=AE,
∴AE=CA,
∴∠E=∠ACE,
∵∠CAB=∠ACE+∠E=2∠E=45°,
∴∠E=22.5°.
故选:A.
12.如图,矩形ABCD中对角线AC与BD相交于点O,DE⊥AC,垂足为点E,若AO:OE=3:2,DE=2,则CE长为( )
A.1
B.2
C.
D.
【分析】由矩形的性质得到∠ADC=90°,BD=AC,OD=BD,OC=AC,求得OC=OD,设OA=3x,OE=2x,得到OD=OA=3x,根据勾股定理即可得到结论.
解:∵四边形ABCD是矩形,
∴AC=BD,OD=BD,OC=AC,∠ADC=90°,
∴OC=OD,
∵AO:OE=3:2,DE⊥AC,
设OA=3x,OE=2x,
在Rt△DOE中,OD2=OE2+DE2,
即,
解得:x=2或x=﹣2(舍去),
∴OC=OA=6,OE=4,
∴EC=OC﹣OE=6﹣4=2,
故选:B.
二、填空题:(本大题共6个小题,每小题3分,满分18分)
13.若使在实数范围内有意义,则x的取值范围为
x<2 .
【分析】根据二次根式有意义时被开方数为非负数,分式的分母不为零列式计算可求解.
解:由题意得6﹣3x>0,
解得x<2,
故答案为x<2.
14.计算3 ÷= .
【分析】利用二次根式乘除法的法则对式子进行运算即可求解.
解:3 ÷
=3÷
=
=.
故答案为:.
15.已知==(b+d≠0),则的值为
.
【分析】根据合比的性质即可求解.
解:∵==(b+d≠0),
∴=.
故答案为:.
16.如图,在平面直角坐标系中,△ABO的顶点都在坐标轴上,OA=4.若△CDO是以原点O为位似图形,△ABO的位似图形(C为点A的对应点),且△CDO与△ABO相似比为,则点C的坐标为
(2,0)或(﹣2,0) .
【分析】先写出A点坐标,然后根据关于原点为位似中心的对应点的坐标关系,把A点的横纵坐标都乘以(或﹣)得到C点坐标.
解:∵OA=4,
∴A(4,0),
∵△CDO是以原点O为位似图形,△ABO的位似图形,且△CDO与△ABO相似比为,
∴C点坐标为(×4,0)或(﹣×4,0),即C(2,0)或(﹣2,0).
故答案为(2,0)或(﹣2,0).
17.若x=2﹣是方程x2﹣4x+c=0的一个根,则c的值是 1 .
【分析】把x=2﹣代入方程x2﹣4x+c=0就得到关于c的方程,就可以解得c的值.
解:把x=2﹣代入方程x2﹣4x+c=0,得(2﹣)2﹣4(2﹣)+c=0,
解得c=1;
故答案为:1.
18.如图,在Rt△ABC纸板中,AC=4,BC=3,P是AC上一点,过点P沿直线剪一次剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是
0<CP≤ .
【分析】分四种情况讨论,依据相似三角形的对应边成比例,即可得到CP长的取值范围.
解:如图所示,过P作PD∥AB交BC于D或PE∥BC交AB于E,则△PCD∽△ACB或△APE∽△ACB,
此时0<CP<4;
如图所示,过P作∠APF=∠B交AB于F,则△APF∽△ABC,
此时0≤CP<4;
如图所示,过P作∠CPG=∠CBA交BC于G,则△CPG∽△CBA,
当点G与点B重合时,CB2=CP×CA,即32=CP×4,
∴CP=,
∴此时,0<CP≤;
综上所述,CP长的取值范围是0<CP≤.
故答案为:0<CP≤.
三、解答题(本大题共7个小题,满分66分)
19.解下列方程:
(1)(x﹣)2=;
(2)x(x﹣2)=(x﹣2);
【分析】(1)由直接开平方法可得出答案;
(2)方程左边因式分解得到两个一元一次方程,解方程即可求出方程的解.
解:(1)原方程可变形为,
∴x1=,x2=;
(2)原方程可变形为x(x﹣2)﹣(x﹣2)=0,
∴=0,
∴x﹣2=0或x﹣=0,
∴x1=2,x2=.
20.已知:如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,DE∥AC,CE∥AD,连接BE,CD.求证:四边形CDBE是正方形.
【分析】根据平行四边形的判定和性质得出DE=AC,CE=AD,进而利用正方形的判定解答即可.
【解答】证明:∵DE∥AC,CE∥AD,
∴四边形ADEC是平行四边形,
∴DE=AC,CE=AD,
∵AD=DB,
∴CE=DB,
∵CE∥DB,
∴四边形DBEC是平行四边形,
∵AC=BC,
∴BC=DE,
∴平行四边形DBEC是矩形,
∵∠ACB=90°,
∴CD=AD=DB,
∴矩形DBEC是正方形.
21.如图,已知在△ABC和△DAC中,∠B=∠DAC,∠D=115°,E,F分别为AB和BC上的点,且EF∥AC,AE=AD,CF=AC.
(1)求∠BAC的度数;
(2)若BC=8,CD=,求的值.
【分析】(1)根据平行线分线段成比例可得,从而得出,可证△ABC∽△DAC,得出答案;
(2)由(1)相似可求出AC=6,E根据F∥AC,可得.
解:(1)∵EF∥AC,
∴,
∵AE=AD,CF=AC,
∴,
∵∠B=∠DAC,
∴△ABC∽△DAC,
∴∠BAC=∠D=115°,
(2)∵△ABC∽△DAC,
∴,
∴=36,
∵AC>0,
∴AC=6,
∴CF=6,
∵EF∥AC,
∴.
22.李先生存入银行4万元,先存一个一年定期,一年后将本息自动转存为一个一年定期,年利率不变,两年后共得本息4.1412万元.
(1)一年定期存款的年利率为多少?(参考数值:=2.035)
(2)若两年定期存款的年利率为2.25%,则李先生4万元存款已得到的利息比按两年定期存款所得利息少多少元?
【分析】(1)设一年定期存款的年利率为x,利用两年后的本息和=本金×(1+年利率)2,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)利用利息=本金×年利率×存款年数,可求出按两年定期存款获得的利润,再将两种存款方式获得的利润做差后即可得出结论.
解:(1)设一年定期存款的年利率为x,
依题意得:4(1+x)2=4.1412,
解得:x1=0.0175=1.75%,x2=﹣2.0175(不合题意,舍去).
答:一年定期存款的年利率为1.75%.
(2)40000×2.25%×2=1800(元),
1800﹣(41412﹣40000)=388(元).
答:李先生4万元存款已得到的利息比按两年定期存款所得利息少388元.
23.如图,在边长为8的正方形ABCD中,点M是边DC上一动点(点M不与边DC端
点重合),点O在边AD上,且OA=OM,作MN⊥MO,交BC于点N.设DM=x,OM=y.
(1)求证:△OMD∽△MNC.
(2)求y关于x的函数表达式.
(3)当x=2时,求△MNC的周长.
【分析】(1)由直角三角形的性质得出∠DOM=∠CMN,根据相似三角形的判定方法可得出结论;
(2)由勾股定理得出(8﹣y)2+x2=y2,则可得出答案;
(3)当x=2时,求出y=,由相似三角形的性质可得出答案.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∴∠DMO+∠DOM=90°,
又∵∠DMO+∠OMN+∠CMN=180°,∠OMN=90°,
∴∠DMO+∠CMN=90°,
∴∠DOM=∠CMN,
∴△OMD∽△MNC;
(2)在Rt△OMD中,OD=AD﹣OA=8﹣y,
由勾股定理得,(8﹣y)2+x2=y2,
∴y=;
(3)当x=2时,y=,
∵OA=OM,
∴△OMD的周长=AD+DM=x+8=2+8=10,OD=8﹣y=8﹣=,
∵△MNC∽△OMD,
∴△MNC的周长:△OMD的周长=MC:OD,
即△MNC的周长:10=(8﹣2):,
∴△MNC的周长=16.
24.如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)是否存在某时刻t使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由;
(2)如果BP=PQ,求此时t的值.
【分析】(1)根据PD∥BC,可得=,所以=,得PD=,由S△APQ=2t×=﹣t2+6t=12,得t2﹣5t+10=0,由△=(﹣5)2﹣4×1×10=﹣15<0,可得不存在某时刻t,使线段PQ恰好把△ABC的面积平分;
(2)根据勾股定理可得QD2+PD2=PQ2,所以得()2+()2=(2t)2,解方程可得t的值.
解:(1)不存在某时刻t,使线段PQ恰好把△ABC的面积平分,理由如下:
如图,过点P作PD⊥AC于点D,
∴PD∥BC,
在Rt△ABC中,∠C=90°,
∵AB=10cm,AC=8cm.
∴BC=6cm,
假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△APQ=S△ABC,
∵S△ABC=AC BC=8×6=24(cm2),
∴S△APQ=12(cm2),
∵PD∥BC,
∴=,
∴=,
∴PD=,
∴S△APQ=2t×=﹣t2+6t,
∴﹣t2+6t=12,
化简得t2﹣5t+10=0,
∵△=(﹣5)2﹣4×1×10=﹣15<0,
∴此方程无实数根,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分;
(2)∵PD∥BC,
∴=,
∴=,
∴AD=,
∵PD=,PQ=BP=2t,
∴QD=AD﹣AQ=﹣2t=,
在Rt△PQD中,根据勾股定理,得
QD2+PD2=PQ2,
∴()2+()2=(2t)2,
化简,得13t2﹣90t+125=0,
解得t1=5,t2=,
∵t=5>4,不符合题意,舍去,
∴t=s.
25.如图,在△ABC中,∠C=90°,AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,过点A作AE⊥AD交BD的延长线于点E,△ABC∽△EDA.
(1)求∠ABC的度数;
(2)求的值.
【分析】(1)依据三角形内角和定理以及角平分线的定义,即可得到∠1+∠2的度数,根据三角形外角性质即可得出∠3的度数,最后根据相似三角形的对应角相等,即可得出结论;
(2)过A作AF⊥DE于点F,设AF=a,易得DE=2a,DF=a,AD=a,BF=a+a,依据勾股定理即可得到AB2=AF2+BF2=(4+2)a2,最后根据相似三角形的面积的比等于相似比的平方,即可得出结论.
解:(1)∵AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,
∴∠1=∠ABC,∠2=∠BAC,
∵∠C=90°,
∴∠1+∠2=(∠ABC+∠BAC)=90°=45°,
∴∠3=∠1+∠2=45°,
∵△ABC∽△EDA,
∴∠ABC=∠3=45°;
(2)过A作AF⊥DE于点F,
∵∠3=45°,AE⊥AD,
∴△ADE是等腰直角三角形,
设AF=a,则DE=2a,DF=a,
Rt△ADF中,AD=a,
∵2∠1=2∠2=45°,
∴∠1=∠2,
∴AD=BD=a,
∴BF=a+a,
在Rt△ABF中,AB2=AF2+BF2=a2+(a+a)2=(4+2)a2,
∵△ABC∽△EDA,
∴===.
同课章节目录
