第2章 机械振动 本章复习提升 Word版含解析
文档属性
| 名称 | 第2章 机械振动 本章复习提升 Word版含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 221.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-08 08:52:12 | ||
图片预览




文档简介
本章复习提升
易混易错练
易错点一 对振幅、位移和路程概念理解不清
1.()一质点做简谐运动,振幅是4
cm、频率是2.5
Hz,某时刻该质点从平衡位置起向正方向运动,经2.5
s质点的位移和路程分别是( )
A.4
cm,24
cm B.-4
cm,100
cm
C.0,100
cm D.4
cm,100
cm
2.()一弹簧振子做简谐运动,周期为T=2
s,在半分钟内振子通过的路程是60
cm,则在此时间内振子经过平衡位置的次数和振子的振幅分别为
( )
A.15次,2
cm B.30次,1
cm
C.15次,1
cm D.60次,2
cm
易错点二 回复力与合外力混淆
3.(河南安阳高二下月考,)如图所示,将弹簧振子从平衡位置拉下一段距离Δx,释放后振子在A、B间振动。设AB=20
cm,振子由A到B运动时间为0.1
s,则下列说法正确的是
( )
A.振子的振幅为20
cm,周期为0.2
s
B.振子在A、B两处受到的回复力分别为kΔx+mg与kΔx-mg
C.振子在A、B两处受到的回复力大小都是kΔx
D.振子完成一次全振动通过的路程是20
cm
4.()(多选)如图所示,一竖直放置的轻弹簧下端固定在水平地面上,质量为m的小球从弹簧正上方高为h处自由下落到弹簧上端A点,然后压缩弹簧到最低点C,若小球放在弹簧上可静止在B点,小球运动过程中空气阻力忽略不计,则下列说法正确的是
( )
A.B点位于A、C连线中点的上方
B.B点位于A、C连线中点的下方
C.小球在A点的回复力等于mg
D.小球在C点的回复力大于mg
易错点三 图像信息提取不准确
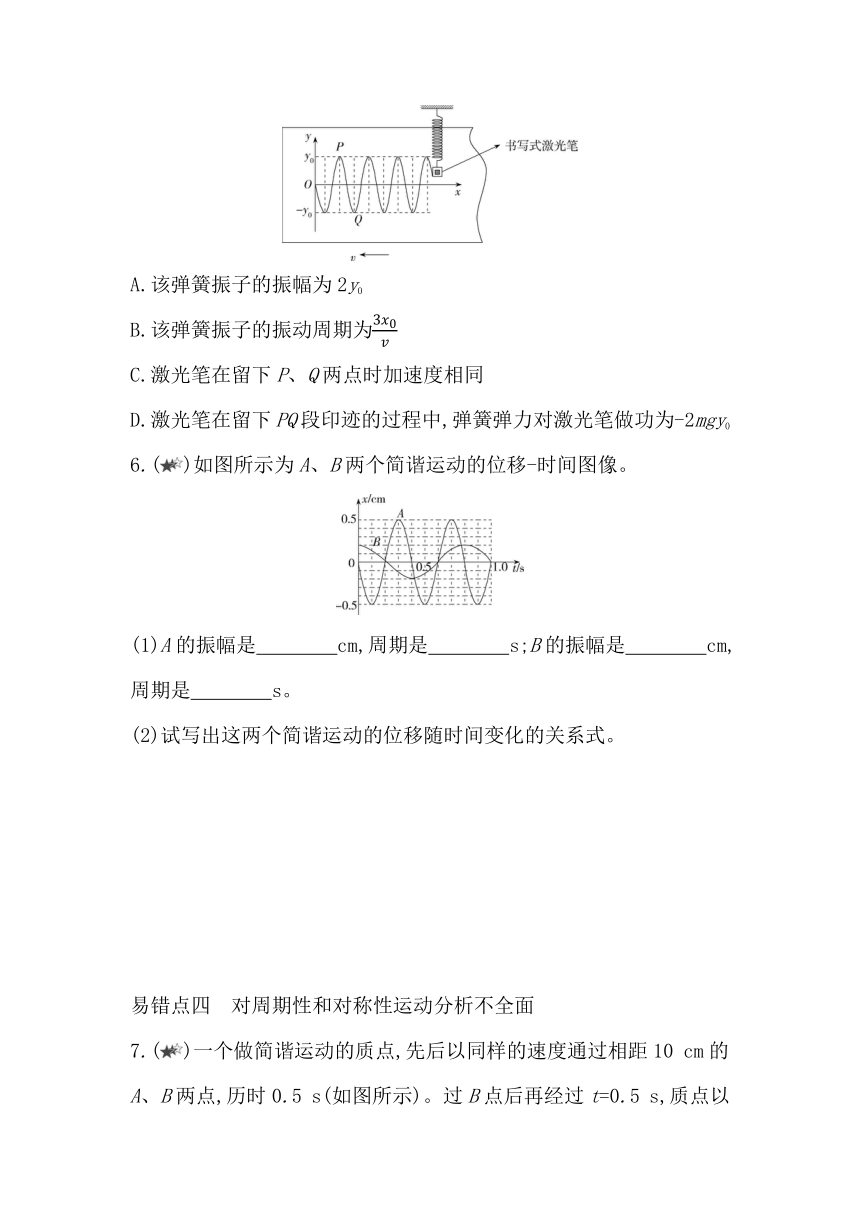
5.(山东临沂十八中高二月考,)如图所示,一轻质弹簧下端系一质量为m的书写式激光笔,组成一弹簧振子,并将其悬挂于教室内一体机白板的前方。使弹簧振子沿竖直方向上下自由振动,白板以速率v水平向左匀速运动,激光笔在白板上留下如图所示的书写印迹。图中相邻竖直虚线的间隔均为x0(未标出),印迹上P、Q两点的纵坐标分别为y0和-y0。忽略空气阻力,重力加速度为g,则
( )
A.该弹簧振子的振幅为2y0
B.该弹簧振子的振动周期为
C.激光笔在留下P、Q两点时加速度相同
D.激光笔在留下PQ段印迹的过程中,弹簧弹力对激光笔做功为-2mgy0
6.()如图所示为A、B两个简谐运动的位移-时间图像。
(1)A的振幅是 cm,周期是 s;B的振幅是 cm,周期是 s。
(2)试写出这两个简谐运动的位移随时间变化的关系式。
易错点四 对周期性和对称性运动分析不全面
7.()一个做简谐运动的质点,先后以同样的速度通过相距10
cm的A、B两点,历时0.5
s(如图所示)。过B点后再经过t=0.5
s,质点以大小相等、方向相反的速度再次通过B点,则质点振动的周期是
( )
A.0.5
s B.1
s C.2
s D.4
s
8.()质点沿x轴做简谐运动,平衡位置为坐标原点O。质点先后经过a点(xa=-5
cm)和b点(xb=5
cm)时速度相同,所用时间tab=0.2
s;质点继续运动由b点回到a点所用的最短时间tba=0.4
s。则该质点做简谐运动的频率为
( )
A.1
Hz B.1.25
Hz C.2
Hz D.2.5
Hz
思想方法练
思想方法一 周期性、对称性思想
1.()(多选)一个质点以O为平衡位置做简谐运动,位移随时间变化的图像如图所示,a、b、c、d表示质点在不同时刻的相应位置,下列说法正确的是
( )
A.质点通过位置b时,相对平衡位置的位移为
B.质点从位置a到c和从位置b到d所用时间相等
C.质点从位置a到b和从位置b到c的平均速度相等
D.质点在b、d两位置速度相同
2.()(多选)一弹簧振子做简谐运动,周期为T。下列说法正确的是
( )
A.若t时刻和(t+Δt)时刻振子运动速度、位移的大小相等、方向相反,则Δt一定等于的奇数倍
B.若t时刻和(t+Δt)时刻振子运动速度的大小相等、方向相反,则Δt一定等于的奇数倍
C.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度一定相等
D.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度可能相等
3.()如图所示,一质点沿水平直线做简谐运动,先后以相同速度通过a、b两点,经历时间tab=1
s,过b点后再经t'=1
s
质点第一次反向通过b点。若在这两秒内质点所通过的路程是8
cm,则该质点的振动周期为 ,振幅为 。
思想方法二 数形结合思想
4.()如图甲所示,一弹簧振子在A、B间做简谐运动,O为平衡位置,图乙是弹簧振子做简谐运动时的位移-时间图像,则关于弹簧振子的加速度随时间的变化规律,下列四个图像中正确的是
( )
5.()在心电图仪、地震仪等仪器工作过程中,要进行振动记录。如图甲所示是一种常用的记录方法,在弹簧振子的小球上安装一支记录用笔P,在下面放一条白纸带,当小球振动时,匀速拉动纸带(纸带速度与振子振动方向垂直),笔就在纸带上画出一条曲线,如图乙所示。若匀速拉动纸带的速度为1
m/s,作出P的振动图像。
6.()如图所示为一单摆的共振曲线,该单摆的摆长约为多少 共振时单摆的振幅多大 共振时摆球的最大速度和最大加速度各为多少 (g取10
m/s2)
答案全解全析
本章复习提升
易混易错练
1.D 周期T==
s=0.4
s,t=2.5
s=6T,质点在2.5
s时到达正向最大位移处,故位移为4
cm,路程为x=6×4A+A=25A=100
cm。
2.B 振子完成一次全振动经过轨迹上每个位置两次(最大位移处除外),而每次全振动振子通过的路程为4个振幅,由此分析可知B正确。
3.C 振子在A、B间振动,AB=20
cm,故振幅为10
cm,选项A错误;根据F=-kx可知振子在A、B两处受到的回复力大小都为kΔx,B错误,C正确;振子完成一次全振动经过的路程为40
cm,D错误。
4.ACD 小球放在弹簧上,可以静止于B点,可知B点为平衡位置,若小球从A点由静止释放,平衡位置在A点和最低点连线的中点,而小球从弹簧的正上方自由下落,最低点需下移,但是平衡位置不变,可知B点位于A、C连线中点的上方,故A项正确,B项错误;小球在A点所受弹力为零,则小球在A点所受的合力为mg,即回复力为mg,故C项正确;若从A点由静止释放小球,到达最低点时的加速度与在A点的加速度对称,大小为g,但是C点所处的位置在A点关于平衡位置对称点的下方,小球在C点的回复力大于mg,故D项正确。
5.D 白板匀速运动,振子振动的周期等于白板运动位移2x0所用的时间,则振动周期T=,振幅为A=y0,A、B错误。加速度是矢量,激光笔在留下P、Q两点时加速度大小相等,方向相反,C错误。在激光笔留下PQ段印迹的过程中,根据动能定理可知,合外力做功为零,由于重力做正功为2mgy0,故弹力对激光笔做负功,为-2mgy0,D正确。故选D。
6.答案 (1)0.5 0.4 0.2 0.8 (2)xA=0.5
sin(5πt+π)cm,xB=0.2
sin
cm
解析 (1)由题图知:A的振幅是0.5
cm,周期是0.4
s;B的振幅是0.2
cm,周期是0.8
s。
(2)由题图知,φA=π,由TA=0.4
s,得ωA==5π
rad/s,则A简谐运动的表达式为xA=0.5
sin(5πt+π)
cm。同样由题图可看出φB=,由TB=0.8
s,得ωB==2.5π
rad/s,则B简谐运动的表达式为xB=0.2
sincm。
7.C 根据题意,由振动的对称性可知:AB的中点(设为O)为平衡位置,A、B两点对称分布于O点两侧,如图所示。质点从平衡位置O向右运动到B的时间tOB=×0.5
s=0.25
s。质点从B向右运动到右方最大位移处(设为D)的时间tBD=×0.5
s=0.25
s。所以,质点从O到D的时间tOD=T=0.25
s+0.25
s=0.5
s,所以T=2
s。故选C。
8.B 由题意可知:a、b两点在O点的两侧,关于O点对称,质点由a点到b点所用时间tab=0.2
s,再由b点回到a点所用最短时间tba=0.4
s,表明质点经过b点后还要继续向x轴的正方向运动,振幅大于5
cm,设周期为T,由简谐运动的对称性可知,tba=,即=0.4
s,T=0.8
s,频率f==
Hz=1.25
Hz,B项正确。
思想方法练
1.BD 质点通过位置b时,相对平衡位置的位移大于,选项A错误;质点从位置a到c和从位置b到d所用时间相等,选项B正确;质点从位置a到b和从位置b到c所用时间相等,位移不相等,所以平均速度不相等,选项C错误;由简谐运动的对称性知选项D正确。
2.AD 若Δt=或Δt=nT-(n=1,2,3…),则在t和(t+Δt)两时刻振子必在关于平衡位置对称的两位置(包括平衡位置),这两时刻,振子的位移、速度均大小相等、方向相反,但在这两时刻弹簧的长度并不一定相等[只有当振子在t和(t+Δt)两时刻均在平衡位置时,弹簧长度才相等]。反过来,若在t和(t+Δt)两时刻振子的位移和速度均大小相等、方向相反,则Δt一定等于的奇数倍,即Δt=(2n-1)(n=1,2,3…)。如果仅仅是振子的速度在t和(t+Δt)两时刻大小相等、方向相反,那么不能得出以上结论。根据以上分析,B、C错误,A、D正确。
3.答案 4
s 4
cm
解析 简谐运动是以平衡位置为中心的对称运动,因为通过a、b两点时的速度相同,所以a、b连线的中点(设为O)必是振动的平衡位置。如图所示,根据简谐运动的对称性可知,从质点反向通过b点到返回a点所用的时间必与从a点到b点所用的时间相同,即tba=tab=1
s,质点从a点经左方最大位移处d再返回a点所用的时间tada必与质点从b点经右方最大位移处c再返回b点所用的时间tbcb相等,即tada=tbcb=t'=1
s。综上所述,质点的振动周期为T=tab+tbcb+tba+tada=4
s。由图和简谐运动的对称性可知,质点在一个周期内通过的路程为s=2
易混易错练
易错点一 对振幅、位移和路程概念理解不清
1.()一质点做简谐运动,振幅是4
cm、频率是2.5
Hz,某时刻该质点从平衡位置起向正方向运动,经2.5
s质点的位移和路程分别是( )
A.4
cm,24
cm B.-4
cm,100
cm
C.0,100
cm D.4
cm,100
cm
2.()一弹簧振子做简谐运动,周期为T=2
s,在半分钟内振子通过的路程是60
cm,则在此时间内振子经过平衡位置的次数和振子的振幅分别为
( )
A.15次,2
cm B.30次,1
cm
C.15次,1
cm D.60次,2
cm
易错点二 回复力与合外力混淆
3.(河南安阳高二下月考,)如图所示,将弹簧振子从平衡位置拉下一段距离Δx,释放后振子在A、B间振动。设AB=20
cm,振子由A到B运动时间为0.1
s,则下列说法正确的是
( )
A.振子的振幅为20
cm,周期为0.2
s
B.振子在A、B两处受到的回复力分别为kΔx+mg与kΔx-mg
C.振子在A、B两处受到的回复力大小都是kΔx
D.振子完成一次全振动通过的路程是20
cm
4.()(多选)如图所示,一竖直放置的轻弹簧下端固定在水平地面上,质量为m的小球从弹簧正上方高为h处自由下落到弹簧上端A点,然后压缩弹簧到最低点C,若小球放在弹簧上可静止在B点,小球运动过程中空气阻力忽略不计,则下列说法正确的是
( )
A.B点位于A、C连线中点的上方
B.B点位于A、C连线中点的下方
C.小球在A点的回复力等于mg
D.小球在C点的回复力大于mg
易错点三 图像信息提取不准确
5.(山东临沂十八中高二月考,)如图所示,一轻质弹簧下端系一质量为m的书写式激光笔,组成一弹簧振子,并将其悬挂于教室内一体机白板的前方。使弹簧振子沿竖直方向上下自由振动,白板以速率v水平向左匀速运动,激光笔在白板上留下如图所示的书写印迹。图中相邻竖直虚线的间隔均为x0(未标出),印迹上P、Q两点的纵坐标分别为y0和-y0。忽略空气阻力,重力加速度为g,则
( )
A.该弹簧振子的振幅为2y0
B.该弹簧振子的振动周期为
C.激光笔在留下P、Q两点时加速度相同
D.激光笔在留下PQ段印迹的过程中,弹簧弹力对激光笔做功为-2mgy0
6.()如图所示为A、B两个简谐运动的位移-时间图像。
(1)A的振幅是 cm,周期是 s;B的振幅是 cm,周期是 s。
(2)试写出这两个简谐运动的位移随时间变化的关系式。
易错点四 对周期性和对称性运动分析不全面
7.()一个做简谐运动的质点,先后以同样的速度通过相距10
cm的A、B两点,历时0.5
s(如图所示)。过B点后再经过t=0.5
s,质点以大小相等、方向相反的速度再次通过B点,则质点振动的周期是
( )
A.0.5
s B.1
s C.2
s D.4
s
8.()质点沿x轴做简谐运动,平衡位置为坐标原点O。质点先后经过a点(xa=-5
cm)和b点(xb=5
cm)时速度相同,所用时间tab=0.2
s;质点继续运动由b点回到a点所用的最短时间tba=0.4
s。则该质点做简谐运动的频率为
( )
A.1
Hz B.1.25
Hz C.2
Hz D.2.5
Hz
思想方法练
思想方法一 周期性、对称性思想
1.()(多选)一个质点以O为平衡位置做简谐运动,位移随时间变化的图像如图所示,a、b、c、d表示质点在不同时刻的相应位置,下列说法正确的是
( )
A.质点通过位置b时,相对平衡位置的位移为
B.质点从位置a到c和从位置b到d所用时间相等
C.质点从位置a到b和从位置b到c的平均速度相等
D.质点在b、d两位置速度相同
2.()(多选)一弹簧振子做简谐运动,周期为T。下列说法正确的是
( )
A.若t时刻和(t+Δt)时刻振子运动速度、位移的大小相等、方向相反,则Δt一定等于的奇数倍
B.若t时刻和(t+Δt)时刻振子运动速度的大小相等、方向相反,则Δt一定等于的奇数倍
C.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度一定相等
D.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度可能相等
3.()如图所示,一质点沿水平直线做简谐运动,先后以相同速度通过a、b两点,经历时间tab=1
s,过b点后再经t'=1
s
质点第一次反向通过b点。若在这两秒内质点所通过的路程是8
cm,则该质点的振动周期为 ,振幅为 。
思想方法二 数形结合思想
4.()如图甲所示,一弹簧振子在A、B间做简谐运动,O为平衡位置,图乙是弹簧振子做简谐运动时的位移-时间图像,则关于弹簧振子的加速度随时间的变化规律,下列四个图像中正确的是
( )
5.()在心电图仪、地震仪等仪器工作过程中,要进行振动记录。如图甲所示是一种常用的记录方法,在弹簧振子的小球上安装一支记录用笔P,在下面放一条白纸带,当小球振动时,匀速拉动纸带(纸带速度与振子振动方向垂直),笔就在纸带上画出一条曲线,如图乙所示。若匀速拉动纸带的速度为1
m/s,作出P的振动图像。
6.()如图所示为一单摆的共振曲线,该单摆的摆长约为多少 共振时单摆的振幅多大 共振时摆球的最大速度和最大加速度各为多少 (g取10
m/s2)
答案全解全析
本章复习提升
易混易错练
1.D 周期T==
s=0.4
s,t=2.5
s=6T,质点在2.5
s时到达正向最大位移处,故位移为4
cm,路程为x=6×4A+A=25A=100
cm。
2.B 振子完成一次全振动经过轨迹上每个位置两次(最大位移处除外),而每次全振动振子通过的路程为4个振幅,由此分析可知B正确。
3.C 振子在A、B间振动,AB=20
cm,故振幅为10
cm,选项A错误;根据F=-kx可知振子在A、B两处受到的回复力大小都为kΔx,B错误,C正确;振子完成一次全振动经过的路程为40
cm,D错误。
4.ACD 小球放在弹簧上,可以静止于B点,可知B点为平衡位置,若小球从A点由静止释放,平衡位置在A点和最低点连线的中点,而小球从弹簧的正上方自由下落,最低点需下移,但是平衡位置不变,可知B点位于A、C连线中点的上方,故A项正确,B项错误;小球在A点所受弹力为零,则小球在A点所受的合力为mg,即回复力为mg,故C项正确;若从A点由静止释放小球,到达最低点时的加速度与在A点的加速度对称,大小为g,但是C点所处的位置在A点关于平衡位置对称点的下方,小球在C点的回复力大于mg,故D项正确。
5.D 白板匀速运动,振子振动的周期等于白板运动位移2x0所用的时间,则振动周期T=,振幅为A=y0,A、B错误。加速度是矢量,激光笔在留下P、Q两点时加速度大小相等,方向相反,C错误。在激光笔留下PQ段印迹的过程中,根据动能定理可知,合外力做功为零,由于重力做正功为2mgy0,故弹力对激光笔做负功,为-2mgy0,D正确。故选D。
6.答案 (1)0.5 0.4 0.2 0.8 (2)xA=0.5
sin(5πt+π)cm,xB=0.2
sin
cm
解析 (1)由题图知:A的振幅是0.5
cm,周期是0.4
s;B的振幅是0.2
cm,周期是0.8
s。
(2)由题图知,φA=π,由TA=0.4
s,得ωA==5π
rad/s,则A简谐运动的表达式为xA=0.5
sin(5πt+π)
cm。同样由题图可看出φB=,由TB=0.8
s,得ωB==2.5π
rad/s,则B简谐运动的表达式为xB=0.2
sincm。
7.C 根据题意,由振动的对称性可知:AB的中点(设为O)为平衡位置,A、B两点对称分布于O点两侧,如图所示。质点从平衡位置O向右运动到B的时间tOB=×0.5
s=0.25
s。质点从B向右运动到右方最大位移处(设为D)的时间tBD=×0.5
s=0.25
s。所以,质点从O到D的时间tOD=T=0.25
s+0.25
s=0.5
s,所以T=2
s。故选C。
8.B 由题意可知:a、b两点在O点的两侧,关于O点对称,质点由a点到b点所用时间tab=0.2
s,再由b点回到a点所用最短时间tba=0.4
s,表明质点经过b点后还要继续向x轴的正方向运动,振幅大于5
cm,设周期为T,由简谐运动的对称性可知,tba=,即=0.4
s,T=0.8
s,频率f==
Hz=1.25
Hz,B项正确。
思想方法练
1.BD 质点通过位置b时,相对平衡位置的位移大于,选项A错误;质点从位置a到c和从位置b到d所用时间相等,选项B正确;质点从位置a到b和从位置b到c所用时间相等,位移不相等,所以平均速度不相等,选项C错误;由简谐运动的对称性知选项D正确。
2.AD 若Δt=或Δt=nT-(n=1,2,3…),则在t和(t+Δt)两时刻振子必在关于平衡位置对称的两位置(包括平衡位置),这两时刻,振子的位移、速度均大小相等、方向相反,但在这两时刻弹簧的长度并不一定相等[只有当振子在t和(t+Δt)两时刻均在平衡位置时,弹簧长度才相等]。反过来,若在t和(t+Δt)两时刻振子的位移和速度均大小相等、方向相反,则Δt一定等于的奇数倍,即Δt=(2n-1)(n=1,2,3…)。如果仅仅是振子的速度在t和(t+Δt)两时刻大小相等、方向相反,那么不能得出以上结论。根据以上分析,B、C错误,A、D正确。
3.答案 4
s 4
cm
解析 简谐运动是以平衡位置为中心的对称运动,因为通过a、b两点时的速度相同,所以a、b连线的中点(设为O)必是振动的平衡位置。如图所示,根据简谐运动的对称性可知,从质点反向通过b点到返回a点所用的时间必与从a点到b点所用的时间相同,即tba=tab=1
s,质点从a点经左方最大位移处d再返回a点所用的时间tada必与质点从b点经右方最大位移处c再返回b点所用的时间tbcb相等,即tada=tbcb=t'=1
s。综上所述,质点的振动周期为T=tab+tbcb+tba+tada=4
s。由图和简谐运动的对称性可知,质点在一个周期内通过的路程为s=2
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
