2020-2021学年北师大版八年级数学上册第一章勾股定理章末测试(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学上册第一章勾股定理章末测试(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 424.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 11:51:38 | ||
图片预览



文档简介
勾股定理
章末测试
一、单选题(每小题
3分,共36分)
1.下列各组数中,是勾股数的是(
)
A.9,16,25
B.1,1,
C.1,,2
D.8,15,17
2.一个直角三角形两条直角边的长分别为6,8,则其斜边上的高为( )
A.
B.13
C.
D.25
3.如图,在单位为1的正方形网格图中有a,b,c,d四条线段,从中任取三条线段所构成的三角形中恰好是直角三角形的个数为( )
A.1个
B.2个
C.3个
D.4个
4.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口处出发先往东走,又往北走,遇到障碍后又往西走,再向北走到处往东拐,仅走了,就找到了宝藏,则门口到藏宝点的直线距离是(
)
A.20km
B.14km
C.11km
D.10km
5.如图所示,是用4个全等的直角三角形与1个正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用,表示直角三角形的两直角边(),下列四个说法:①,②,③,④.其中说法正确的是(
)
A.①②③
B.①②④
C.②③④
D.①②③④
6.如图长方体木箱的长、宽、高分别为12m,4m,3m,则能放进木箱中的木棒最长为(
)
A.19m
B.24m
C.13m
D.15m
7.本期,我们学习了用赵爽弦图证明勾股定理在如图所示的赵爽弦图中,在上取点使得,连接、.若正方形的面积为,则与的面积之差为(
)
A.
B.
C.
D.不确定
8.如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.2.5m
B.3m
C.3.5m
D.4m
9.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?“意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?(
)
A.4尺
B.4.55尺
C.5.45尺
D.5.55尺
10.如图,一艘轮船以的速度从港口出发,向东北方向航行,另一艘轮船以的速度同时从港口出发,向东南方向航行,出发后,两船的距离是(
)
A.
B.
C.
D.
11.如图,牧童在处放牛,牧童家在处,、处距河岸的距离、的长分别为500m和700m,且,两点的距离为500m,天黑前牧童从处将牛牵到河边饮水再回家,那么牧童最少要走的距离为(
)
A.1000m
B.1200m
C.1300m
D.1700m
12.如图,是一种饮料的包装盒,长、宽、高分别为、、,现有一长为的吸管插入到盒的底部,则吸管漏在盒外面的部分的取值范围为(
)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
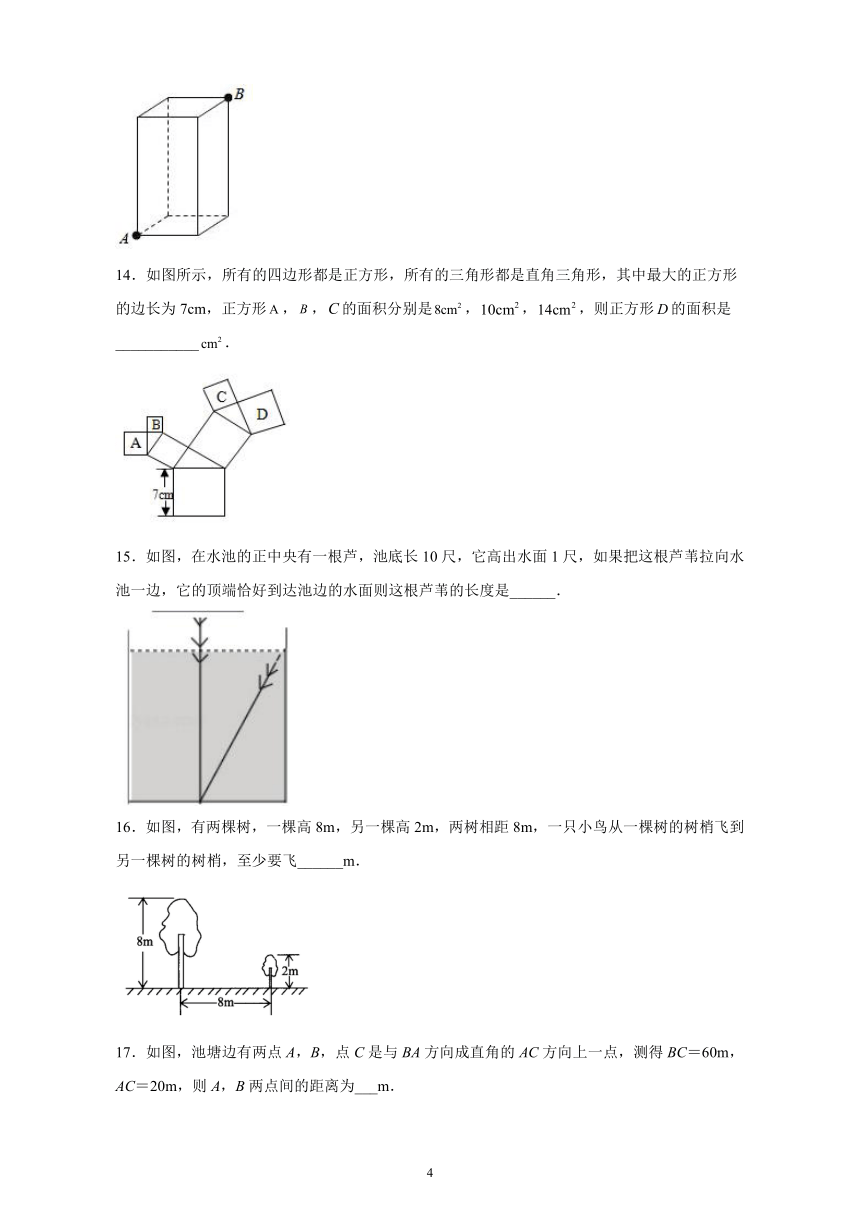
13.如图,一只蚂蚁从长为2cm,宽为2cm,高为3cm的长方形纸箱的A点沿纸箱爬到B点,那么它所行的最短路线长是___cm.
14.如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形,,的面积分别是,,,则正方形的面积是___________.
15.如图,在水池的正中央有一根芦,池底长10尺,它高出水面1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是______.
16.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少要飞______m.
17.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,则A,B两点间的距离为___m.
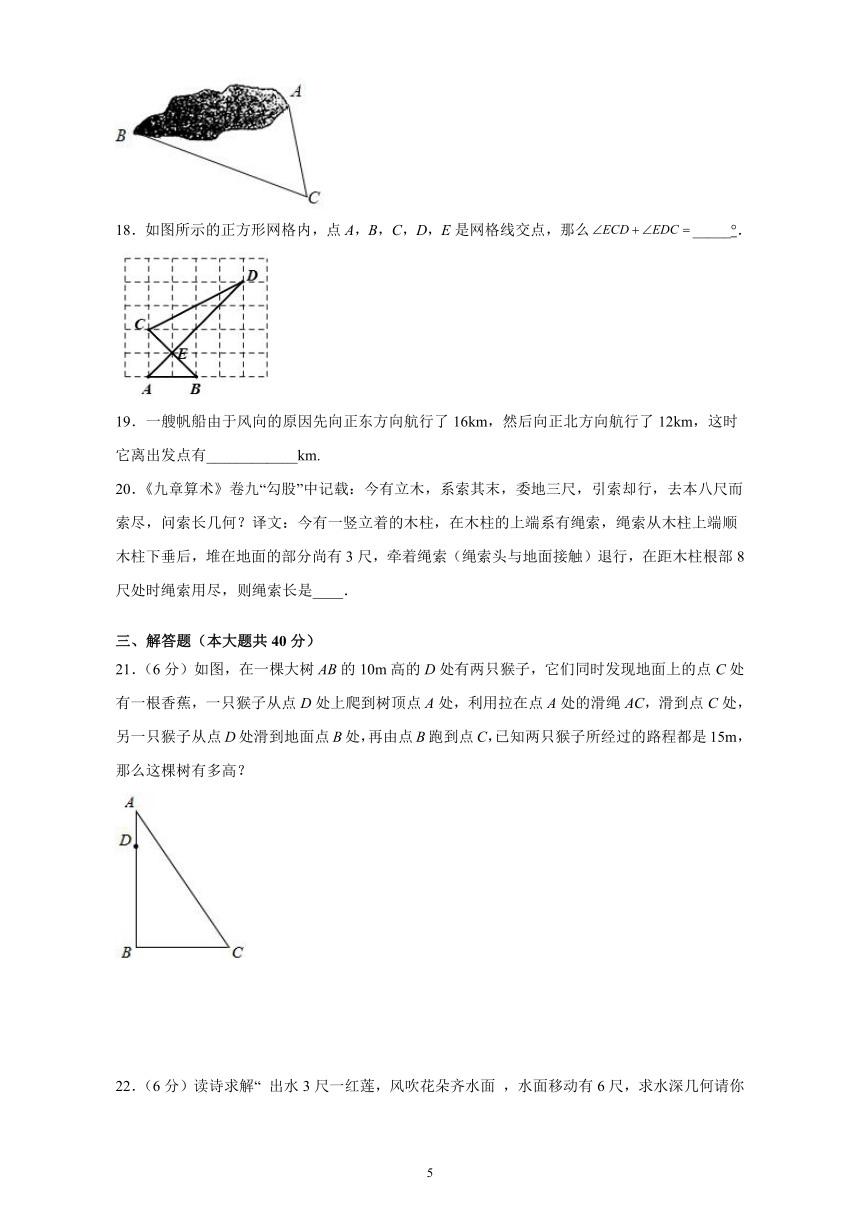
18.如图所示的正方形网格内,点A,B,C,D,E是网格线交点,那么_____°.
19.一艘帆船由于风向的原因先向正东方向航行了16km,然后向正北方向航行了12km,这时它离出发点有____________km.
20.《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽,则绳索长是____.
三、解答题(本大题共40分)
21.(6分)如图,在一棵大树AB的10m高的D处有两只猴子,它们同时发现地面上的点C处有一根香蕉,一只猴子从点D处上爬到树顶点A处,利用拉在点A处的滑绳AC,滑到点C处,另一只猴子从点D处滑到地面点B处,再由点B跑到点C,已知两只猴子所经过的路程都是15m,那么这棵树有多高?
22.(6分)读诗求解“
出水3尺一红莲,风吹花朵齐水面
,水面移动有6尺,求水深几何请你算”.
23.(6分)如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
24.(6分)如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点D的位置,问船向岸边移动了多少米.(假设绳子是直的)
25.(8分)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索(或)的长度.
26.(8分)如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的底端B在水平方向上向右滑动了多远?
参考答案
1.D
解:A、92+162≠252,不是勾股数,故此选项不合题意;
B、不是正整数,不是勾股数,故此选项不合题意;
C、不是正整数,不是勾股数,故此选项不合题意;
D、82+152=172,都是正整数,是勾股数,故此选项符合题意;
故选:D.
2.C
解:设斜边为c,斜边上的高为h,
∵直角三角形两条直角边的长分别为6,8,
∴,
∴,
∴;
故选C.
3.B
解:由图可得,
线段a,b,c,d的长度分别为:,,,,
∴,
∴从a,b,c,d四条线段中任取三条线段所构成的三角形中恰好是直角三角形的个数为2,
故选:B.
4.D
解:过点B作BC⊥AC,且AC,BC交于C点,
∴∠ACB=90°,
由图中可以得:AC=(8-3+1)千米=6千米,BC=(2+6)千米=8千米,
在Rt△ABC中,AC=6千米,BC=8千米
则根据勾股定理千米,
故选D.
5.A
解:①∵△ABC为直角三角形,
∴根据勾股定理:x2+y2=AB2=49,故本选项正确;
②由图可知,x y=CE==2,故本选项正确;
③由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积,
列出等式为4××xy+4=49,即2xy+4=49;
故本选项正确;
④由2xy+4=49可得2xy=45①,
又∵x2+y2=49②,
∴①+②得,x2+2xy+y2=49+45,
整理得,(x+y)2=94,
x+y=≠9,
故本选项错误.
∴正确结论有①②③.
故选A.
6.C
解:如图所示,连接AC,AG,
由长方体的性质可以知∠ACG=∠ABC=90°,
∴(
m),
∴(
m),
∴能放进木箱中的木棒最长为13m,
故选C.
7.A
解:由赵爽弦图可知,
正方形的边长为,,,
∴,
∵
∴,
故选:A.
8.C
解:由勾股定理得:
AB=,
因为地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
所以地毯的长度至少是1.5+2=3.5(m).
故选C.
9.B
解:设竹子折断处离地面x尺,则斜边为(10 x)尺,
根据勾股定理得:x2+32=(10 x)2,
解得:x=4.55.
故选B.
10.A
解:∵两船分别沿东北及东南方向行驶,
∴∠BAC=90°,
设2小时后沿东北方向行驶的轮船到达B点,沿东南方向行驶的轮船到达C点,连接BC,
∵一轮船以8nmile/h的速度从港口A出发向东北方向航行,另一轮船以6nmile/h的速度同时从港口出发向东南方向航行,
∴AB=8×2=16nmile,AC=6×2=12nmile,
∵∠BAC=90°,
∴BC=nmile.
故选A.
11.C
解:解:作A关于CD的对称点E,连接BE,并作BF⊥AC于点F.
则EF=BD+AC=500+700=1200m,BF=CD=500m.
在Rt△BEF中,根据勾股定理得:BE==1300(m).
故选:C.
12.B
解:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16 12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线长==5cm,高为12cm,
由勾股定理可得:杯里面管长==13cm,则露在杯口外的长度最短为16 13=3(cm),
∴
故选:B.
13.5
解:(1)如图所示,将长方体正面与上底面展开后,由勾股定理可得:
;
(2)如图所示,将长方体正面与右侧面展开后,由勾股定理可得:
;
∵,
∴最短路线长为5cm,
故答案为:5.
14.17
解:∵所有的三角形都是直角三角形,所有的四边形都是正方形,
∴正方形A的面积,正方形B的面积,正方形C的面积,正方形D的面积,
∵,,
∴正方形A、B、C、D的面积和,
即,
解得:.
故答案为:17.
15.13尺
解:设水深为x尺,则芦苇长为(x+1)尺,
根据勾股定理得:x2+()2=(x+1)2,
解得:x=12,
芦苇的长度=x+1=12+1=13(尺),
故答案为:13尺.
16.10
解:两棵树的高度差为8m-2m=6m,间距为8m
根据勾股定理可得:小鸟至少飞行的距离m.
故答案为:10.
17.
解:在Rt△ABC
中,∠CAB=90゜,AC=20m,BC=60m,由勾股定理得:
(m)
即A、B两点间的距离为m.
故答案为:.
18.90
解:设正方形网格边长为a,
由勾股定理求得,
∴
∴为直角三角形,
即
故答案为:90.
19.20
解:如图,
A为出发点,B为正东方向航行了16km的地点,C为向正北方向航行了12km的地点,
故AB=16km,BC=12km,
在Rt△ABC中,由勾股定理得:km,
即这时它离出发点有20km,
故答案为20.
20.尺
解:设绳索长为x尺,根据题意有,
,
解得,
故答案为:尺.
21.
解:设树高AB为x
m.
由题意知BC=15-10=5(m),AD=(x-10)m,AC=15-AD=15-x+10=(25-x)m.
在
Rt△ABC中,AB2+BC2=AC2,
即x2+52=(25-x)2,解得x=12.
答:这棵树有12
m高.
22.4.5
尺
解:设水深AP=x尺,PB=PC=(x+3)尺,
根据勾股定理得:PA +AC =PC ,x +6 =(x+3) .
解得:x=4.5,
答∶水深
4.5
尺.
23.北偏东45°(或西北)
解:由题意可得:RP=18海里,PQ=24海里,QR=30海里,
∵182+242=302,
∴△RPQ是直角三角形,
∴∠RPQ=90°,
∵“远航”号沿东北方向航行,即沿北偏东45°方向航行,
∴∠RPS=45°,
∴“海天”号沿北偏西45°(或西北)方向航行.
24.船向岸边移动了9米.
解:在Rt△ABC中:
∵∠CAB=90°,BC=17米,AC=8米,
∴AB==15(米),
∵此人以1米每秒的速度收绳,7秒后船移动到点D的位置,
∴CD=17-1×7=10(米),
∴AD==6(米),
∴BD=AB-AD=15-6=9(米),
答:船向岸边移动了9米.
25.秋千绳索的长度为尺.
解:设尺,
由题可知:尺,尺,
∴(尺),尺,
在中,尺,尺,尺,
由勾股定理得:,
解得:,
则秋千绳索的长度为尺.
26.(1)2.4米;(2)1.3m
解:(1)∵∠C=90°,AB=2.5,BC=0.7,
∴AC==(米),
答:此时梯顶A距地面的高度AC是2.4米;
(2)∵梯子的顶端A下滑了0.9米至点A′,
∴A′C=AC A′A=2.4 0.9=1.5(m),
在Rt△A′CB′中,由勾股定理得:A′C2+B′C2=A′B′2,
∴1.52+B′C2=2.52,
∴B′C=2(m),
∴BB′=CB′ BC=2 0.7=1.3(m),
答:梯子的底端B在水平方向滑动了1.3m.
章末测试
一、单选题(每小题
3分,共36分)
1.下列各组数中,是勾股数的是(
)
A.9,16,25
B.1,1,
C.1,,2
D.8,15,17
2.一个直角三角形两条直角边的长分别为6,8,则其斜边上的高为( )
A.
B.13
C.
D.25
3.如图,在单位为1的正方形网格图中有a,b,c,d四条线段,从中任取三条线段所构成的三角形中恰好是直角三角形的个数为( )
A.1个
B.2个
C.3个
D.4个
4.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口处出发先往东走,又往北走,遇到障碍后又往西走,再向北走到处往东拐,仅走了,就找到了宝藏,则门口到藏宝点的直线距离是(
)
A.20km
B.14km
C.11km
D.10km
5.如图所示,是用4个全等的直角三角形与1个正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用,表示直角三角形的两直角边(),下列四个说法:①,②,③,④.其中说法正确的是(
)
A.①②③
B.①②④
C.②③④
D.①②③④
6.如图长方体木箱的长、宽、高分别为12m,4m,3m,则能放进木箱中的木棒最长为(
)
A.19m
B.24m
C.13m
D.15m
7.本期,我们学习了用赵爽弦图证明勾股定理在如图所示的赵爽弦图中,在上取点使得,连接、.若正方形的面积为,则与的面积之差为(
)
A.
B.
C.
D.不确定
8.如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.2.5m
B.3m
C.3.5m
D.4m
9.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?“意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?(
)
A.4尺
B.4.55尺
C.5.45尺
D.5.55尺
10.如图,一艘轮船以的速度从港口出发,向东北方向航行,另一艘轮船以的速度同时从港口出发,向东南方向航行,出发后,两船的距离是(
)
A.
B.
C.
D.
11.如图,牧童在处放牛,牧童家在处,、处距河岸的距离、的长分别为500m和700m,且,两点的距离为500m,天黑前牧童从处将牛牵到河边饮水再回家,那么牧童最少要走的距离为(
)
A.1000m
B.1200m
C.1300m
D.1700m
12.如图,是一种饮料的包装盒,长、宽、高分别为、、,现有一长为的吸管插入到盒的底部,则吸管漏在盒外面的部分的取值范围为(
)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
13.如图,一只蚂蚁从长为2cm,宽为2cm,高为3cm的长方形纸箱的A点沿纸箱爬到B点,那么它所行的最短路线长是___cm.
14.如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形,,的面积分别是,,,则正方形的面积是___________.
15.如图,在水池的正中央有一根芦,池底长10尺,它高出水面1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是______.
16.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少要飞______m.
17.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,则A,B两点间的距离为___m.
18.如图所示的正方形网格内,点A,B,C,D,E是网格线交点,那么_____°.
19.一艘帆船由于风向的原因先向正东方向航行了16km,然后向正北方向航行了12km,这时它离出发点有____________km.
20.《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽,则绳索长是____.
三、解答题(本大题共40分)
21.(6分)如图,在一棵大树AB的10m高的D处有两只猴子,它们同时发现地面上的点C处有一根香蕉,一只猴子从点D处上爬到树顶点A处,利用拉在点A处的滑绳AC,滑到点C处,另一只猴子从点D处滑到地面点B处,再由点B跑到点C,已知两只猴子所经过的路程都是15m,那么这棵树有多高?
22.(6分)读诗求解“
出水3尺一红莲,风吹花朵齐水面
,水面移动有6尺,求水深几何请你算”.
23.(6分)如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
24.(6分)如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点D的位置,问船向岸边移动了多少米.(假设绳子是直的)
25.(8分)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索(或)的长度.
26.(8分)如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的底端B在水平方向上向右滑动了多远?
参考答案
1.D
解:A、92+162≠252,不是勾股数,故此选项不合题意;
B、不是正整数,不是勾股数,故此选项不合题意;
C、不是正整数,不是勾股数,故此选项不合题意;
D、82+152=172,都是正整数,是勾股数,故此选项符合题意;
故选:D.
2.C
解:设斜边为c,斜边上的高为h,
∵直角三角形两条直角边的长分别为6,8,
∴,
∴,
∴;
故选C.
3.B
解:由图可得,
线段a,b,c,d的长度分别为:,,,,
∴,
∴从a,b,c,d四条线段中任取三条线段所构成的三角形中恰好是直角三角形的个数为2,
故选:B.
4.D
解:过点B作BC⊥AC,且AC,BC交于C点,
∴∠ACB=90°,
由图中可以得:AC=(8-3+1)千米=6千米,BC=(2+6)千米=8千米,
在Rt△ABC中,AC=6千米,BC=8千米
则根据勾股定理千米,
故选D.
5.A
解:①∵△ABC为直角三角形,
∴根据勾股定理:x2+y2=AB2=49,故本选项正确;
②由图可知,x y=CE==2,故本选项正确;
③由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积,
列出等式为4××xy+4=49,即2xy+4=49;
故本选项正确;
④由2xy+4=49可得2xy=45①,
又∵x2+y2=49②,
∴①+②得,x2+2xy+y2=49+45,
整理得,(x+y)2=94,
x+y=≠9,
故本选项错误.
∴正确结论有①②③.
故选A.
6.C
解:如图所示,连接AC,AG,
由长方体的性质可以知∠ACG=∠ABC=90°,
∴(
m),
∴(
m),
∴能放进木箱中的木棒最长为13m,
故选C.
7.A
解:由赵爽弦图可知,
正方形的边长为,,,
∴,
∵
∴,
故选:A.
8.C
解:由勾股定理得:
AB=,
因为地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
所以地毯的长度至少是1.5+2=3.5(m).
故选C.
9.B
解:设竹子折断处离地面x尺,则斜边为(10 x)尺,
根据勾股定理得:x2+32=(10 x)2,
解得:x=4.55.
故选B.
10.A
解:∵两船分别沿东北及东南方向行驶,
∴∠BAC=90°,
设2小时后沿东北方向行驶的轮船到达B点,沿东南方向行驶的轮船到达C点,连接BC,
∵一轮船以8nmile/h的速度从港口A出发向东北方向航行,另一轮船以6nmile/h的速度同时从港口出发向东南方向航行,
∴AB=8×2=16nmile,AC=6×2=12nmile,
∵∠BAC=90°,
∴BC=nmile.
故选A.
11.C
解:解:作A关于CD的对称点E,连接BE,并作BF⊥AC于点F.
则EF=BD+AC=500+700=1200m,BF=CD=500m.
在Rt△BEF中,根据勾股定理得:BE==1300(m).
故选:C.
12.B
解:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16 12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线长==5cm,高为12cm,
由勾股定理可得:杯里面管长==13cm,则露在杯口外的长度最短为16 13=3(cm),
∴
故选:B.
13.5
解:(1)如图所示,将长方体正面与上底面展开后,由勾股定理可得:
;
(2)如图所示,将长方体正面与右侧面展开后,由勾股定理可得:
;
∵,
∴最短路线长为5cm,
故答案为:5.
14.17
解:∵所有的三角形都是直角三角形,所有的四边形都是正方形,
∴正方形A的面积,正方形B的面积,正方形C的面积,正方形D的面积,
∵,,
∴正方形A、B、C、D的面积和,
即,
解得:.
故答案为:17.
15.13尺
解:设水深为x尺,则芦苇长为(x+1)尺,
根据勾股定理得:x2+()2=(x+1)2,
解得:x=12,
芦苇的长度=x+1=12+1=13(尺),
故答案为:13尺.
16.10
解:两棵树的高度差为8m-2m=6m,间距为8m
根据勾股定理可得:小鸟至少飞行的距离m.
故答案为:10.
17.
解:在Rt△ABC
中,∠CAB=90゜,AC=20m,BC=60m,由勾股定理得:
(m)
即A、B两点间的距离为m.
故答案为:.
18.90
解:设正方形网格边长为a,
由勾股定理求得,
∴
∴为直角三角形,
即
故答案为:90.
19.20
解:如图,
A为出发点,B为正东方向航行了16km的地点,C为向正北方向航行了12km的地点,
故AB=16km,BC=12km,
在Rt△ABC中,由勾股定理得:km,
即这时它离出发点有20km,
故答案为20.
20.尺
解:设绳索长为x尺,根据题意有,
,
解得,
故答案为:尺.
21.
解:设树高AB为x
m.
由题意知BC=15-10=5(m),AD=(x-10)m,AC=15-AD=15-x+10=(25-x)m.
在
Rt△ABC中,AB2+BC2=AC2,
即x2+52=(25-x)2,解得x=12.
答:这棵树有12
m高.
22.4.5
尺
解:设水深AP=x尺,PB=PC=(x+3)尺,
根据勾股定理得:PA +AC =PC ,x +6 =(x+3) .
解得:x=4.5,
答∶水深
4.5
尺.
23.北偏东45°(或西北)
解:由题意可得:RP=18海里,PQ=24海里,QR=30海里,
∵182+242=302,
∴△RPQ是直角三角形,
∴∠RPQ=90°,
∵“远航”号沿东北方向航行,即沿北偏东45°方向航行,
∴∠RPS=45°,
∴“海天”号沿北偏西45°(或西北)方向航行.
24.船向岸边移动了9米.
解:在Rt△ABC中:
∵∠CAB=90°,BC=17米,AC=8米,
∴AB==15(米),
∵此人以1米每秒的速度收绳,7秒后船移动到点D的位置,
∴CD=17-1×7=10(米),
∴AD==6(米),
∴BD=AB-AD=15-6=9(米),
答:船向岸边移动了9米.
25.秋千绳索的长度为尺.
解:设尺,
由题可知:尺,尺,
∴(尺),尺,
在中,尺,尺,尺,
由勾股定理得:,
解得:,
则秋千绳索的长度为尺.
26.(1)2.4米;(2)1.3m
解:(1)∵∠C=90°,AB=2.5,BC=0.7,
∴AC==(米),
答:此时梯顶A距地面的高度AC是2.4米;
(2)∵梯子的顶端A下滑了0.9米至点A′,
∴A′C=AC A′A=2.4 0.9=1.5(m),
在Rt△A′CB′中,由勾股定理得:A′C2+B′C2=A′B′2,
∴1.52+B′C2=2.52,
∴B′C=2(m),
∴BB′=CB′ BC=2 0.7=1.3(m),
答:梯子的底端B在水平方向滑动了1.3m.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
