初中数学人教版九年级上册24.1.4 圆周角-同步试题精编(word解析版)
文档属性
| 名称 | 初中数学人教版九年级上册24.1.4 圆周角-同步试题精编(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 287.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 17:51:04 | ||
图片预览




文档简介
24.1.4圆周角
知识点1
圆周角定理
例1.如图,是的直径,为圆内一点,则下列说法中正确的是(
)
A.是的弦
B.是圆心角
C.是圆周角
D.
变式2.如图,在中,点是上一点,若,则的度数是(
)
A.80°
B.100°
C.120°
D.130°
3.AB是⊙O的直径,C、D是圆上两点,∠BDC=32°,则∠AOC的度数为(
)
A.32°
B.64°
C.116°
D.128°
知识点2
同弧或等弧所对的圆周角相等
例4.如图,、是的直径,,交于点,,则的度数为(
)
A.20°
B.40°
C.60°
D.70°
变式5.如图,是的直径,点,在圆上,,则等于(
)
A.
B.
C.
D.
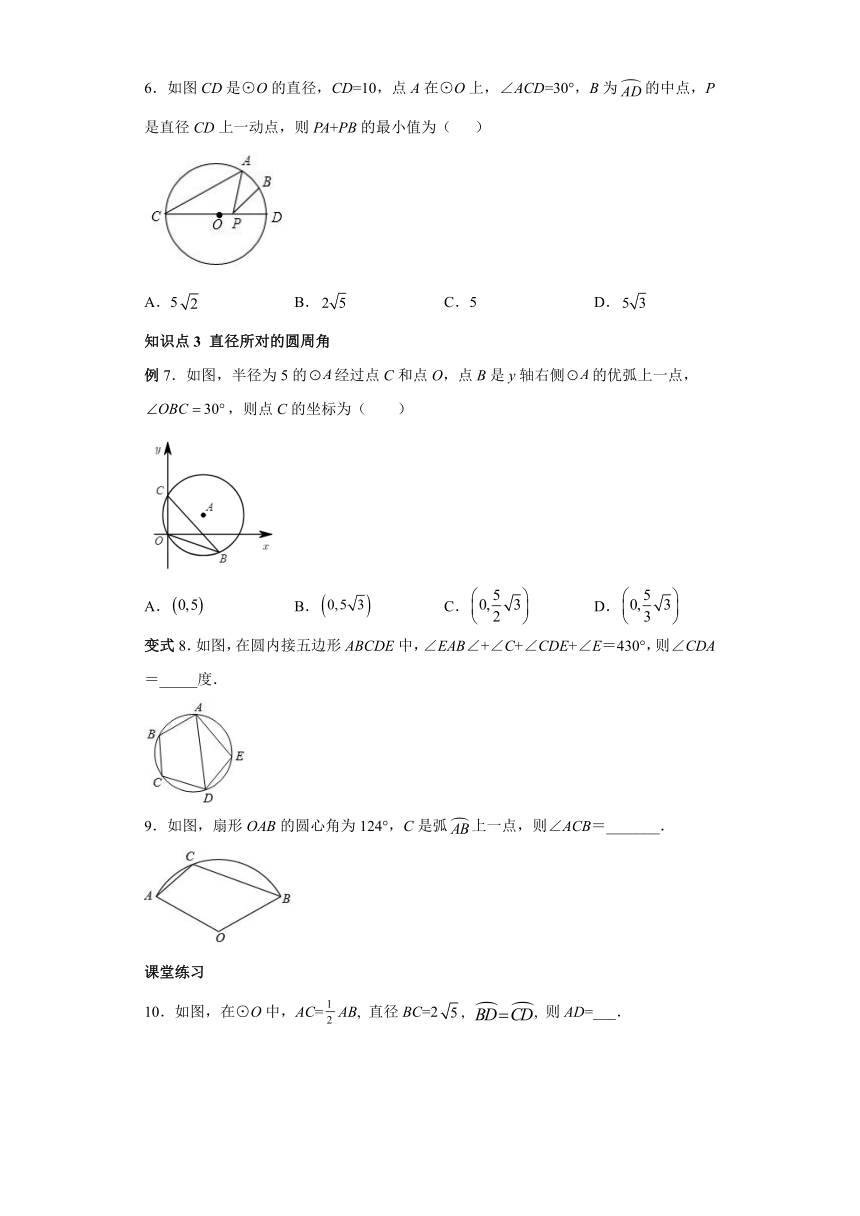
6.如图CD是⊙O的直径,CD=10,点A在⊙O上,∠ACD=30°,B为的中点,P是直径CD上一动点,则PA+PB的最小值为(
)
A.5
B.
C.5
D.
知识点3
直径所对的圆周角
例7.如图,半径为5的经过点C和点O,点B是y轴右侧的优弧上一点,,则点C的坐标为(
)
A.
B.
C.
D.
变式8.如图,在圆内接五边形ABCDE中,∠EAB∠+∠C+∠CDE+∠E=430°,则∠CDA=_____度.
9.如图,扇形OAB的圆心角为124°,C是弧上一点,则∠ACB=_______.
课堂练习
10.如图,在⊙O中,AC=AB,
直径BC=2,
,
则AD=___.
11.如下是小华设计的“作的角平分线”的尺规作图过程,请帮助小华完成尺规作图并填空(保留作图痕迹).
步骤
作法
推断
第一步
在上任取一点C,以点C为圆心,为半径作半圆,分别交射线于点P,点Q,连接
①
,理由是
②
第二步
过点C作的垂线,交于点D,交于点E
,
③
第三步
作射线
射线平分
射线为所求作.
12.如图,△ABC是⊙O的内接三角形,点C是优弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β,
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给以证明.
13.如图所示,已知AB为圆O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=2cm,CD=8cm,求圆O的直径.
14.如图,⊙O是△ABD的外接圆,AB为直径,点C是弧AD的中点,连接OC,BC分别交AD于点F,E.
(1)求证:∠ABD=2∠C.
(2)若AB=10,BC=8,求BD的长.
试卷第4页,总4页
参考答案
1.B
【分析】
根据弦、圆心角、圆周角的概念可直接进行排除选项.
【详解】
解:A、点C不在上,所以AC不是的弦,故错误,不符合题意;
B、因为点O是圆心,所以∠BOC是圆心角,故正确,符合题意;
C、点C不在上,所以∠C不是圆周角,故错误,故不符合题意;
D、当点C在圆上时,则OC=OA=OB,若成立,则AC+OC<OA+OB,
∴AC<OA,与题干矛盾,
∴D选项错误,不符合题意;
故选B.
【点睛】
本题主要考查弦、圆心角、圆周角的概念,熟练掌握弦、圆心角、圆周角的概念是解题的关键.
2.D
【分析】
在优弧AC上取点D,连接AD、CD,由∠AOC=
100°
求出∠ADC=
∠AOC,根据四边形ABCD是圆内接四边形,得到∠ADC+∠ABC=
180°
,即可求出∠ABC的度数.
【详解】
在优弧AC上取点D,连接AD、CD,
∵∠AOC=
100°
,
∴∠ADC=
∠AOC=50°
,
∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=
180°
,
∴∠ABC=
180°
-50°
=130°
,
故选:D.
【点睛】
此题考查圆周角定理:同弧所对的圆周角等于圆心角的一半,圆内接四边形的性质:圆内接四边形的对角互补.
3.C
【分析】
根据圆周角定理可求∠AOC,根据邻补角定义可求∠AOC的度数.
【详解】
∵AB是⊙O的直径,C、D是圆上两点,∠BDC=32°
∴∠BOC=2∠D=2×32°=64°
∴∠AOC=180°-∠BOC=116°
故选:C
【点睛】
考核知识点:圆周角定理.理解圆周角定理是关键.
4.C
【分析】
先根据圆周角定理可得∠EOD=2∠A=40°,再根据平行线的性质可得∠ADB=∠A=20°,由三角形外角定理即可得出答案.
【详解】
解:∵∠A=20°,
∴∠EOD=2∠A=40°,
又∵,
∴∠ADB=∠A=20°,
∴∠AFC=∠EOD+∠ADB=40°+20°=60°.
故选:C.
【点睛】
本题主要考查了圆周角定理,熟练应用圆周角定理进行求解是解决本题的关键.
5.B
【分析】
由圆周角定理得出∠ACB=90°,由直角三角形的性质求出∠B=55°,再由圆周角定理得出∠ADC=∠B=55°即可.
【详解】
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=35°,
∴∠B=90°﹣35°=55°,
∴∠ADC=∠B=55°.
故选:B.
【点睛】
此题主要考查了三角形的外接圆、圆周角定理以及直角三角形的性质;熟练掌握圆周角定理是解题的关键.
6.A
【分析】
首先作A关于CD的对称点Q,连接BQ,然后根据圆周角定理、圆的对称性质和勾股定理解答.本题考查的是轴对称-最短路线问题,解答此题的关键是找到点A的对称点,把题目的问题转化为两点之间线段最短解答.
【详解】
解:作A关于MN的对称点Q,连接CQ,BQ,BQ交CD于P,
此时AP+PB=QP+PB=QB,
根据两点之间线段最短,PA+PB的最小值为QB的长度,
连接OQ,OB,
∵B为的中点,
∴∠BOD=∠ACD=30°,
∴∠QOD=2∠QCD=2×30°=60°,
∴∠BOQ=30°+60°=90°.
∵直径CD=10,
∴OB=CD=×10=5,
∴BQ===5,即PA+PB的最小值为5
.
故选A.
【点睛】
此题主要考查圆周角定理的应用,解题的关键是熟知圆周角定理、圆的对称性质应用.
7.A
【分析】
先根据可得CD是的直径,进而求得,再利用圆周角定理得出∠CDO的度数,进而利用含30°的直角三角形的性质得出答案.
【详解】
解:如图,设与x轴的交点为D,连接CD.
∴CD是的直径,
∵的半径为5,
,
,
,
∴点C的坐标为,
故选:A.
【点睛】
此题主要考查了圆周角定理及其推论以及含30°的直角三角形的性质,作出正确的辅助线是解决本题的关键.
8.70
【分析】
先利用多边的内角和得到∠EAB+∠B+∠C+∠CDE+∠E=540°,则可计算出∠B=110°,然后根据圆内接四边形的性质求∠CDA的度数.
【详解】
解:∵五边形ABCDE的内角和为(5-2)×180°=540°,
∴∠EAB+∠B+∠C+∠CDE+∠E=540°,
∵∠EAB+∠C+∠CDE+∠E=430°,
∴∠B=540°-430°=110°,
∵四边形ABCD为⊙O的内接四边形,
∴∠B+∠CDA=180°,
∴∠CDA=180°-110°=70°.
故答案为70.
【点睛】
本题考查了多边形的内角和与圆内接四边形的性质,运用圆内接四边形的性质是解决问题的关键.
9.118°
【分析】
在⊙O上取点D,连接AD,BD,根据圆周角定理求出∠D的度数,由圆内接四边形的性质即可得出结论.
【详解】
解:如图所示,在⊙O上取点D,连接AD,BD,
∵∠AOB=124°,
∴∠ADB=∠AOB=×124°=62°.
∵四边形ADBC是圆内接四边形,
∴∠ACB=180°﹣62°=118°.
故答案为:118°.
【点睛】
本题主要考查了圆内接四边形的性质,圆心角与它的圆周角的关系,解题的关键在于能够熟练掌握相关知识进行求解.
10.
【分析】
过D点作DE⊥AB交AB于E,连接BD,DC,根据和BC是直径可以得到,∠DAB=∠DAC=45°=∠DBC=∠DCB,即可得到AE=DE,利用勾股定理先求出AB,BD再求出AE,即可求出AD.
【详解】
解:如图所示,过D点作DE⊥AB交AB于E,连接BD,CD
∵BC是圆的直径
∴∠BAC=90°=∠BDC
∵
∴∠DAB=∠DAC=45°=∠DBC=∠DCB
∴BD=DC
∵DE⊥AB
∴∠AED=90°
∴∠EDA=∠DAB=45°
∴AE=DE
在Rt△ABC中,AC=AB,BC=2,
∴
∴
同理
∴
∴
设AE=DE=x,则BE=4-x
在Rt△DEB中,
∴
解得或
∵,
∴
∴
∴
∴
∴AE=DE=3
∴
故答案为:.
【点睛】
本题主要考查了圆周角定理,直径所对的圆周角是90°,勾股定理,等腰三角形的判定等等,大角对大边,解题的关键在于能够熟练掌握相关知识进行求解.
11.见解析;①90;②直径所对的圆周角是直角;③
【分析】
根据直径所对的圆周角是直角,和同弧所对的圆周角相等即可得出结论
【详解】
解:补全的图形如图1所示.
①∵OQ是直径
∴∠OPQ=90°
故答案为:90;
②故答案为:直径所对的圆周角是直角;
③∵CE⊥PQ
∴由垂径定理得:.
故答案为:
【点睛】
本题考查圆周角定理的推论,垂径定理,熟练掌握圆周角定理及推论是关键
12.(1)55°;(2)α+β=90°,证明见解析.
【分析】
(1)连接OB,根据等腰三角形的性质得到∠OBA=35°,根据三角形内角和定理求出∠AOB,根据圆周角定理计算即可;
(2)根据三角形内角和定理和圆周角定理计算.
【详解】
解:(1)连接OB,
∵∠OAB=α=35°,
∴∠OBA=35°,
∴∠AOB=110°,
∴β=∠AOB=55°;
(2)结论:α+β=90°.
证明:∵∠AOB=180°-2α,β=∠AOB
∴β=90°-α,
∴α+β=90°.
【点睛】
本题考查的是三角形的外接圆与外心,掌握圆周角定理、三角形内角和定理是解题的关键.
13.(1)翙解析;(2)圆O的直径为10cm.
【分析】
(1)由AB为⊙O的直径,AB⊥CD,根据垂径定理即可得,然后由圆周角定理可得∠BCD=∠BAC,又由OA=OC,根据等边对等角,可得∠BAC=∠ACO,继而证得结论;
(2)根据勾股定理,求出各边之间的关系,即可确定半径.
【详解】
(1)证明:∵AB为⊙O的直径,AB⊥CD,
∴,
∴∠BCD=∠BAC,
∵OA=OC,
∴∠BAC=∠ACO,
∴∠ACO=∠BCD;
(2)设⊙O的半径为Rcm,则OE=OB-EB=(R-2)cm,
CE=CD=×8=4(cm).
在Rt△CEO中,由勾股定理可得
OC2=OE2+CE2,即R2=(R-2)2+42,
解得R=5,
∴OB=5cm.
故圆O的直径为10cm.
【点睛】
本题考查圆周角定理、垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题.
14.(1)见解析;(2)BD=2.8
【分析】
(1)利用弧的中点,等腰三角形的性质计算即可.
(2)利用勾股定理,三角形中位线定理,垂径定理的推论计算即可.
【详解】
(1)证明:∵C是的中点,
∴,
∴∠ABC=∠CBD,
∵OB=OC,
∴∠ABC=∠C,
∴∠ABC=∠CBD=∠C,
∴∠ABD=∠ABC+∠CBD=2∠C;
(2)解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC==6,
∵C是的中点,
∴OC⊥AD,
∴,
∴,
∴OF=1.4,
又∵O是AB的中点,F是AD的中点,
∴OF是△ABD的中位线,
∴BD=2OF=2.8.
【点睛】
本题考查了垂径定理及其推论,直径所对的圆周角是直角,勾股定理,三角形中位线定理,熟练掌握垂径定理,灵活运用勾股定理和三角形中位线定理是解题的关键.
答案第11页,总11页
知识点1
圆周角定理
例1.如图,是的直径,为圆内一点,则下列说法中正确的是(
)
A.是的弦
B.是圆心角
C.是圆周角
D.
变式2.如图,在中,点是上一点,若,则的度数是(
)
A.80°
B.100°
C.120°
D.130°
3.AB是⊙O的直径,C、D是圆上两点,∠BDC=32°,则∠AOC的度数为(
)
A.32°
B.64°
C.116°
D.128°
知识点2
同弧或等弧所对的圆周角相等
例4.如图,、是的直径,,交于点,,则的度数为(
)
A.20°
B.40°
C.60°
D.70°
变式5.如图,是的直径,点,在圆上,,则等于(
)
A.
B.
C.
D.
6.如图CD是⊙O的直径,CD=10,点A在⊙O上,∠ACD=30°,B为的中点,P是直径CD上一动点,则PA+PB的最小值为(
)
A.5
B.
C.5
D.
知识点3
直径所对的圆周角
例7.如图,半径为5的经过点C和点O,点B是y轴右侧的优弧上一点,,则点C的坐标为(
)
A.
B.
C.
D.
变式8.如图,在圆内接五边形ABCDE中,∠EAB∠+∠C+∠CDE+∠E=430°,则∠CDA=_____度.
9.如图,扇形OAB的圆心角为124°,C是弧上一点,则∠ACB=_______.
课堂练习
10.如图,在⊙O中,AC=AB,
直径BC=2,
,
则AD=___.
11.如下是小华设计的“作的角平分线”的尺规作图过程,请帮助小华完成尺规作图并填空(保留作图痕迹).
步骤
作法
推断
第一步
在上任取一点C,以点C为圆心,为半径作半圆,分别交射线于点P,点Q,连接
①
,理由是
②
第二步
过点C作的垂线,交于点D,交于点E
,
③
第三步
作射线
射线平分
射线为所求作.
12.如图,△ABC是⊙O的内接三角形,点C是优弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β,
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给以证明.
13.如图所示,已知AB为圆O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=2cm,CD=8cm,求圆O的直径.
14.如图,⊙O是△ABD的外接圆,AB为直径,点C是弧AD的中点,连接OC,BC分别交AD于点F,E.
(1)求证:∠ABD=2∠C.
(2)若AB=10,BC=8,求BD的长.
试卷第4页,总4页
参考答案
1.B
【分析】
根据弦、圆心角、圆周角的概念可直接进行排除选项.
【详解】
解:A、点C不在上,所以AC不是的弦,故错误,不符合题意;
B、因为点O是圆心,所以∠BOC是圆心角,故正确,符合题意;
C、点C不在上,所以∠C不是圆周角,故错误,故不符合题意;
D、当点C在圆上时,则OC=OA=OB,若成立,则AC+OC<OA+OB,
∴AC<OA,与题干矛盾,
∴D选项错误,不符合题意;
故选B.
【点睛】
本题主要考查弦、圆心角、圆周角的概念,熟练掌握弦、圆心角、圆周角的概念是解题的关键.
2.D
【分析】
在优弧AC上取点D,连接AD、CD,由∠AOC=
100°
求出∠ADC=
∠AOC,根据四边形ABCD是圆内接四边形,得到∠ADC+∠ABC=
180°
,即可求出∠ABC的度数.
【详解】
在优弧AC上取点D,连接AD、CD,
∵∠AOC=
100°
,
∴∠ADC=
∠AOC=50°
,
∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=
180°
,
∴∠ABC=
180°
-50°
=130°
,
故选:D.
【点睛】
此题考查圆周角定理:同弧所对的圆周角等于圆心角的一半,圆内接四边形的性质:圆内接四边形的对角互补.
3.C
【分析】
根据圆周角定理可求∠AOC,根据邻补角定义可求∠AOC的度数.
【详解】
∵AB是⊙O的直径,C、D是圆上两点,∠BDC=32°
∴∠BOC=2∠D=2×32°=64°
∴∠AOC=180°-∠BOC=116°
故选:C
【点睛】
考核知识点:圆周角定理.理解圆周角定理是关键.
4.C
【分析】
先根据圆周角定理可得∠EOD=2∠A=40°,再根据平行线的性质可得∠ADB=∠A=20°,由三角形外角定理即可得出答案.
【详解】
解:∵∠A=20°,
∴∠EOD=2∠A=40°,
又∵,
∴∠ADB=∠A=20°,
∴∠AFC=∠EOD+∠ADB=40°+20°=60°.
故选:C.
【点睛】
本题主要考查了圆周角定理,熟练应用圆周角定理进行求解是解决本题的关键.
5.B
【分析】
由圆周角定理得出∠ACB=90°,由直角三角形的性质求出∠B=55°,再由圆周角定理得出∠ADC=∠B=55°即可.
【详解】
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=35°,
∴∠B=90°﹣35°=55°,
∴∠ADC=∠B=55°.
故选:B.
【点睛】
此题主要考查了三角形的外接圆、圆周角定理以及直角三角形的性质;熟练掌握圆周角定理是解题的关键.
6.A
【分析】
首先作A关于CD的对称点Q,连接BQ,然后根据圆周角定理、圆的对称性质和勾股定理解答.本题考查的是轴对称-最短路线问题,解答此题的关键是找到点A的对称点,把题目的问题转化为两点之间线段最短解答.
【详解】
解:作A关于MN的对称点Q,连接CQ,BQ,BQ交CD于P,
此时AP+PB=QP+PB=QB,
根据两点之间线段最短,PA+PB的最小值为QB的长度,
连接OQ,OB,
∵B为的中点,
∴∠BOD=∠ACD=30°,
∴∠QOD=2∠QCD=2×30°=60°,
∴∠BOQ=30°+60°=90°.
∵直径CD=10,
∴OB=CD=×10=5,
∴BQ===5,即PA+PB的最小值为5
.
故选A.
【点睛】
此题主要考查圆周角定理的应用,解题的关键是熟知圆周角定理、圆的对称性质应用.
7.A
【分析】
先根据可得CD是的直径,进而求得,再利用圆周角定理得出∠CDO的度数,进而利用含30°的直角三角形的性质得出答案.
【详解】
解:如图,设与x轴的交点为D,连接CD.
∴CD是的直径,
∵的半径为5,
,
,
,
∴点C的坐标为,
故选:A.
【点睛】
此题主要考查了圆周角定理及其推论以及含30°的直角三角形的性质,作出正确的辅助线是解决本题的关键.
8.70
【分析】
先利用多边的内角和得到∠EAB+∠B+∠C+∠CDE+∠E=540°,则可计算出∠B=110°,然后根据圆内接四边形的性质求∠CDA的度数.
【详解】
解:∵五边形ABCDE的内角和为(5-2)×180°=540°,
∴∠EAB+∠B+∠C+∠CDE+∠E=540°,
∵∠EAB+∠C+∠CDE+∠E=430°,
∴∠B=540°-430°=110°,
∵四边形ABCD为⊙O的内接四边形,
∴∠B+∠CDA=180°,
∴∠CDA=180°-110°=70°.
故答案为70.
【点睛】
本题考查了多边形的内角和与圆内接四边形的性质,运用圆内接四边形的性质是解决问题的关键.
9.118°
【分析】
在⊙O上取点D,连接AD,BD,根据圆周角定理求出∠D的度数,由圆内接四边形的性质即可得出结论.
【详解】
解:如图所示,在⊙O上取点D,连接AD,BD,
∵∠AOB=124°,
∴∠ADB=∠AOB=×124°=62°.
∵四边形ADBC是圆内接四边形,
∴∠ACB=180°﹣62°=118°.
故答案为:118°.
【点睛】
本题主要考查了圆内接四边形的性质,圆心角与它的圆周角的关系,解题的关键在于能够熟练掌握相关知识进行求解.
10.
【分析】
过D点作DE⊥AB交AB于E,连接BD,DC,根据和BC是直径可以得到,∠DAB=∠DAC=45°=∠DBC=∠DCB,即可得到AE=DE,利用勾股定理先求出AB,BD再求出AE,即可求出AD.
【详解】
解:如图所示,过D点作DE⊥AB交AB于E,连接BD,CD
∵BC是圆的直径
∴∠BAC=90°=∠BDC
∵
∴∠DAB=∠DAC=45°=∠DBC=∠DCB
∴BD=DC
∵DE⊥AB
∴∠AED=90°
∴∠EDA=∠DAB=45°
∴AE=DE
在Rt△ABC中,AC=AB,BC=2,
∴
∴
同理
∴
∴
设AE=DE=x,则BE=4-x
在Rt△DEB中,
∴
解得或
∵,
∴
∴
∴
∴
∴AE=DE=3
∴
故答案为:.
【点睛】
本题主要考查了圆周角定理,直径所对的圆周角是90°,勾股定理,等腰三角形的判定等等,大角对大边,解题的关键在于能够熟练掌握相关知识进行求解.
11.见解析;①90;②直径所对的圆周角是直角;③
【分析】
根据直径所对的圆周角是直角,和同弧所对的圆周角相等即可得出结论
【详解】
解:补全的图形如图1所示.
①∵OQ是直径
∴∠OPQ=90°
故答案为:90;
②故答案为:直径所对的圆周角是直角;
③∵CE⊥PQ
∴由垂径定理得:.
故答案为:
【点睛】
本题考查圆周角定理的推论,垂径定理,熟练掌握圆周角定理及推论是关键
12.(1)55°;(2)α+β=90°,证明见解析.
【分析】
(1)连接OB,根据等腰三角形的性质得到∠OBA=35°,根据三角形内角和定理求出∠AOB,根据圆周角定理计算即可;
(2)根据三角形内角和定理和圆周角定理计算.
【详解】
解:(1)连接OB,
∵∠OAB=α=35°,
∴∠OBA=35°,
∴∠AOB=110°,
∴β=∠AOB=55°;
(2)结论:α+β=90°.
证明:∵∠AOB=180°-2α,β=∠AOB
∴β=90°-α,
∴α+β=90°.
【点睛】
本题考查的是三角形的外接圆与外心,掌握圆周角定理、三角形内角和定理是解题的关键.
13.(1)翙解析;(2)圆O的直径为10cm.
【分析】
(1)由AB为⊙O的直径,AB⊥CD,根据垂径定理即可得,然后由圆周角定理可得∠BCD=∠BAC,又由OA=OC,根据等边对等角,可得∠BAC=∠ACO,继而证得结论;
(2)根据勾股定理,求出各边之间的关系,即可确定半径.
【详解】
(1)证明:∵AB为⊙O的直径,AB⊥CD,
∴,
∴∠BCD=∠BAC,
∵OA=OC,
∴∠BAC=∠ACO,
∴∠ACO=∠BCD;
(2)设⊙O的半径为Rcm,则OE=OB-EB=(R-2)cm,
CE=CD=×8=4(cm).
在Rt△CEO中,由勾股定理可得
OC2=OE2+CE2,即R2=(R-2)2+42,
解得R=5,
∴OB=5cm.
故圆O的直径为10cm.
【点睛】
本题考查圆周角定理、垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题.
14.(1)见解析;(2)BD=2.8
【分析】
(1)利用弧的中点,等腰三角形的性质计算即可.
(2)利用勾股定理,三角形中位线定理,垂径定理的推论计算即可.
【详解】
(1)证明:∵C是的中点,
∴,
∴∠ABC=∠CBD,
∵OB=OC,
∴∠ABC=∠C,
∴∠ABC=∠CBD=∠C,
∴∠ABD=∠ABC+∠CBD=2∠C;
(2)解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC==6,
∵C是的中点,
∴OC⊥AD,
∴,
∴,
∴OF=1.4,
又∵O是AB的中点,F是AD的中点,
∴OF是△ABD的中位线,
∴BD=2OF=2.8.
【点睛】
本题考查了垂径定理及其推论,直径所对的圆周角是直角,勾股定理,三角形中位线定理,熟练掌握垂径定理,灵活运用勾股定理和三角形中位线定理是解题的关键.
答案第11页,总11页
同课章节目录
