初中数学人教版九年级上册24.2.2 切线长定理及三角形的内切圆-同步试题精编(word解析版)
文档属性
| 名称 | 初中数学人教版九年级上册24.2.2 切线长定理及三角形的内切圆-同步试题精编(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 473.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览



文档简介
24.2.2切线长定理及三角形的内切圆
一.选择题
1.如图,PA、PB切⊙O于点A、B,PA=4,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是(
)
A.4
B.8
C.12
D.16
2.根据尺规作图的痕迹,可以判定点O为的内心的是(
)
A.B.C.
D.
3.如图,在中,是外一点,与相切于两点,是上两点,若,则(
)
A.210°
B.215°
C.220°
D.225°
4.如图PA、PB是圆O的切线,切点分别为A、B,点C在AB上,过C作圆O的切线分别交PA、PB于点D、E,连接OD、OE,若∠P=50°,则∠DOE的度数为( )
A.130°
B.50°
C.60°
D.65°
5.在中,,则这个三角形的外接圆和内切圆半径分别是(
)
A.
B.
C.
D.
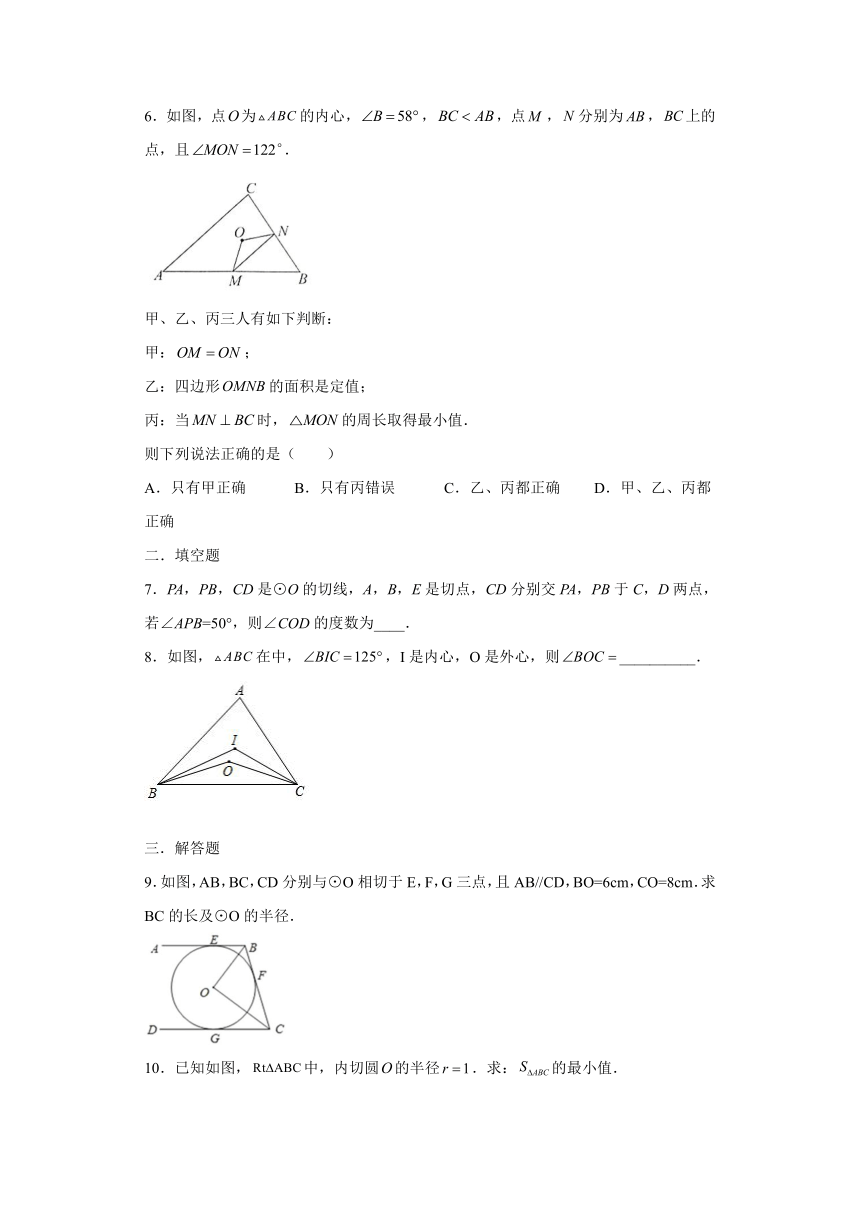
6.如图,点为的内心,,,点,分别为,上的点,且.
甲、乙、丙三人有如下判断:
甲:;
乙:四边形的面积是定值;
丙:当时,的周长取得最小值.
则下列说法正确的是(
)
A.只有甲正确
B.只有丙错误
C.乙、丙都正确
D.甲、乙、丙都正确
二.填空题
7.PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=50°,则∠COD的度数为____.
8.如图,在中,,I是内心,O是外心,则__________.
三.解答题
9.如图,AB,BC,CD分别与⊙O相切于E,F,G三点,且AB//CD,BO=6cm,CO=8cm.求BC的长及⊙O的半径.
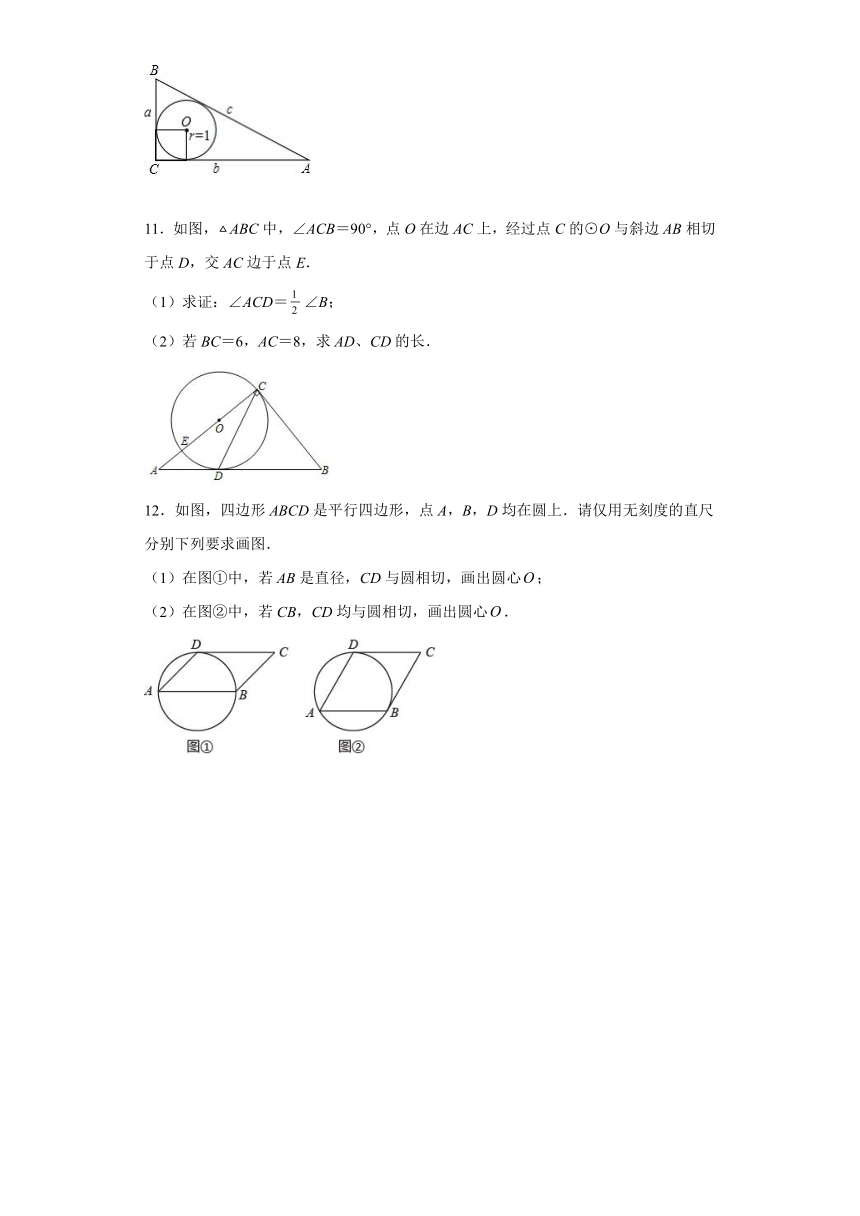
10.已知如图,中,内切圆的半径.求:的最小值.
11.如图,ABC中,∠ACB=90°,点O在边AC上,经过点C的⊙O与斜边AB相切于点D,交AC边于点E.
(1)求证:∠ACD=∠B;
(2)若BC=6,AC=8,求AD、CD的长.
12.如图,四边形ABCD是平行四边形,点A,B,D均在圆上.请仅用无刻度的直尺分别下列要求画图.
(1)在图①中,若AB是直径,CD与圆相切,画出圆心;
(2)在图②中,若CB,CD均与圆相切,画出圆心.
试卷第2页,总3页
参考答案
1.B
【分析】
根据切线长定理即可得结论.
【详解】
解:∵PA、PB切⊙O于点A、B,
∴PB=PA=4,
∵CD切⊙O于点E,交PA、PB于C、D两点,
∴CA=CE,DB=DE,
∴PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=4+4=8.
则△PCD的周长是8.
故选:B.
【点睛】
本题考查了切线长定理,解决本题的关键是掌握切线的性质.
2.C
【分析】
根据三角形的内心定义和基本尺规作图进行判断即可.
【详解】
解:由于三角形的内心是三角形角平分线的交点,由基本作图知选项C中尺规作图作的是 的平分线,所以点O为的内心,
故选:C.
【点睛】
本题考查基本作图、三角形内心定义,熟练掌握基本尺规作图是解答的关键.
3.B
【分析】
连接AB,根据圆内接四边形性质和切线长定理求出和的度数即可.
【详解】
解:连接AB,
∵与相切于两点,
∴,
∵,
∴,
∵是上两点,
∴,
∴;
故选:B.
【点睛】
本题考查了切线长定理、圆内接四边形性质、等腰三角形性质,解题关键是恰当连接辅助线,构造等腰三角形和圆内接四边形.
4.D
【分析】
连接OA、OB、OC,由切线性质得OB⊥PB、OA⊥PA,从而求得∠AOB的度数,再由切线长定理得到DB=DC,从而证得OD平分∠BOC,同理得OE平分∠AOC,最后由∠DOE=∠AOB得到∠DOE的度数.
【详解】
解:如下图
连OA、OB、OC
∵PB切⊙O于B,PA切⊙O于A
∴OB⊥PB,OA⊥PA
又∠P=50°
∴∠AOB=130°
∵DB切⊙O于B,DE切⊙O于C
∴DB=DC且OC⊥DC
∴OD平分∠BOC,即∠DOC=∠BOC
同理得∠EOC=∠AOC
∴∠DOE=∠DOC+∠EOC
=∠BOC+∠AOC
=(∠BOC+∠AOC)
=∠AOB=×130°
=65°.
故选:D.
【点睛】
此题考查切线的性质、切线长定理,发现∠DOE=∠AOB是关键.
5.C
【分析】
首先根据勾股定理逆定理判断△ABC是直角三角形,得其斜边是10,即可求得外接圆半径和内切圆半径.
【详解】
∵AC=6,BC=8,AC=10,,
∴,
∴△ABC是直角三角形,且斜边是AC=10,
∴其外接圆的半径为5,
三角形的内切圆半径=,
故选:C.
【点睛】
本题考查了三角形的外接圆和内切圆,勾股定理的逆定理;解题的关键是灵活运用勾股定理的逆定理判断△ABC是以AC为斜边的直角三角形.
6.B
【分析】
点为的内心,可用角平分线的性质,再用三角形全等可判断甲和乙,当最小,即当时,的周长最小即可判断丙.
【详解】
(1)∵点为的内心,
∴当于,于时,.
当,不垂直于,时,
如图1,过点作于,于.
则.
∵,
∴.∵,
∴.
∵点为的内心,,,
∴.
∴≌.
∴.故甲的判断正确.
(2)如图1,连接.
由(1)可知,四边形的面积为.
∵点的位置固定,
∴四边形的面积是定值.故乙的判断正确.
(3)如图2,过点作于点.
由(1)可得,.
∴的周长.
∴当最小,即当时,的周长最小,此时不垂直于,故丙的判断不正确.
综上所述,答案选B.
【点睛】
此题考查的是三角形的内心,熟悉掌握三角形内心的性质是解题的关键.
7.65°或115°
【分析】
根据题意画出符合题意的图形,分别求出∠AOB,再根据切线的性质求出∠COD的度数.
【详解】
如图,连接OA、OB、OE
∵PA,PB是⊙O的切线
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°
∵∠APB=50°,
∴∠AOB=360°-90°-90°-50°=130°
∵CD是⊙O的切线
∴OE⊥CD
∵∠CEO=∠DEO=90°
∵PA,PB,CD是⊙O的切线,A,B,E是切点,
∴∠OCA=∠OCE,∠ODB=∠ODE,
∵∠AOC=180°-∠OAC-∠OCA,∠EOC=180°-∠OEC-∠OCE,
∴∠AOC=∠EOC
同理可得∠BOD=∠EOD
∴∠COD=∠EOC+∠EOD=∠AOE+∠BOE=∠AOB=65°
如图,连接OA、OB、OE
同理可得∠AOB=130°
同理可得∠COD=∠EOC+∠EOD=∠AOE+∠BOE
∴∠COD=(360°-130°)=115°
故答案为:65°或115°.
【点睛】
此题主要考查考查了切线的性质,切线长定理,三角形的内角和等知识点的应用,解题的关键是根据题意分情况作图求解.
8.140°
【分析】
根据三角形的内心得出,根据三角形内角和定理求出,进而可求得的度数,根据圆周角定理即可求得∠BOC.
【详解】
解:在△ABC中,∠BIC=125°,I是内心,
∴,
∴,
∴
∴,
∵O是外心,
∴,
故答案为:140°.
【点睛】
本题考查了三角形的内切圆和三角形的外接圆,圆周角定理,三角形的内角和定理等知识点.正确识别图中相关角是解题关键.
9.BC=10cm,半径为cm.
【分析】
由切线长定理和可证明是直角三角形,在Rt
中,由勾股定理可求得BC长.连接OF,利用等积法可求得OF的长,OF即为半径长.
【详解】
(1)∵AB、BC、CD是的切线
∴BF=BE,CF=CG,∠OBC=∠ABC,∠BCO=∠BCD
∵
∴∠ABC+∠BCD=
∴∠OBC+∠BCO=
∴∠BOC=
∴是直角三角形
∵BO=6,CO=8
∴
∴BC的长为10cm.
(2)连接OF,
∵BC与相切与点F
∴
利用面积可得:
∴
∴的半径为cm.
【点睛】
本题主要考察切线长定理,求得是直角是解题的关键.
10.最小值是.
【分析】
根据Rt△ABC中,内切圆O的半径r,三角形三个边分别为:a、b、c,可得S△ABC=ab,ab=2S△,2r=a+b c,c=a+b 2r,再根据勾股定理列出方程,根据一元二次方程根的判别式即可求解.
【详解】
解:∵中,内切圆的半径,三角形三个边分别为:、、,
∴.
设,
∴.
∵,
∴.
∴.
两边平方,得,
.
将,代入,得:
,.
∵且,
∴,是方程的两个根.
∵,是正实数,
∴△,即.
.
解得或,不合题意舍去.
∴的最小值是.
【点睛】
本题考查了三角形的内切圆与内心的应用,解决本题的关键是综合运用三角形内切圆的性质、一元二次方程根的判别式等知识.
11.(1)见解析;(2)4,
【分析】
(1)连接OD,如图,根据切线的性质得到∠ODB=90°,∠ABC+∠COD=180°,再根据等角的补角得到∠AOD=∠ABC,然后根据圆周角定理得到∠AOD=2∠ACD,从而得到结论;
(2)先利用勾股定理计算出在AB=10,再利用切线长定理得到BD=BC=6,利用线段差可得AD=4,设⊙O的半径为r,则OD=OC=r,OA=8﹣r,利用勾股定理得到r2+42=(8﹣r)2,解得r=3,连接OB交CD于H,如图,则OB垂直平分CD,然后利用面积法可计算出CH,从而得到CD的长.
【详解】
(1)证明:连接OD,如图,
∵AB为切线,
∴OD⊥AB,
∴∠ODB=90°,
∵∠ACB=90°,
∴∠ABC+∠COD=180°,
∵∠AOD+∠COD=180°,
∴∠AOD=∠ABC,
∵OD=OC,
∴∠OCD=∠ODC,
∵∠AOD=∠OCD+∠ODC
=2∠ACD,
∴∠ACD=∠ABC;
(2)解:在Rt△ABC中,AB==10,
∵OC⊥CB,OC为半径,
∴BC为切线,
∴BD=BC=6,
∴AD=4,
设⊙O的半径为r,则OD=OC=r,OA=8﹣r,
在Rt△AOD中,r2+42=(8﹣r)2,
解得r=3,
∴OC=3,
连接OB交CD于H,如图,
∵OC=OD,BC=BD,
∴OB垂直平分CD,
在Rt△OCB中,OB=,
∵OB CH=OC BC,
∴CH=,
∴CD=2CH=.
【点睛】
本题考查切线性质,四边形内角和,等角的补角性质,圆周角定理,等腰三角形性质,外角性质,勾股定理,切线长定理,三角形面积掌握并会利用这些知识是解题关键.
12.(1)见解析;(2)见解析
【分析】
(1)延长CB交圆于一点,把这点与点D连接,与AB交点即为圆心;
(2)连接AC、BD交于点G,AC交圆于点E,射线DE交BC于F,射线FG交DA于H,连接BH交AC于O即可.
【详解】
(1)如图1所示,延长CB交圆于点E,连接DE,与AB交点即为圆心;
由已知可得∠A+∠DBA=90°,∠EBA=∠C=∠A,故∠EBA
+∠DBA=90°,DE为直径;
(2)如图2所示,连接AC、BD交于点G,AC交圆于点E,射线DE交BC于F,射线FG交DA于H,连接BH交AC于O.点即为所求.说明:由已知可得,△ADB为等边三角形,由作图可知,AE为直径,DF⊥BC,可得,F是BC中点,进而得出H是AD中点,BH⊥AD,BH过圆心;
【点睛】
本题考查了无刻度直尺作图,解题关键是准确理解题意,根据圆的有关性质进行作图.
答案第12页,总12页
一.选择题
1.如图,PA、PB切⊙O于点A、B,PA=4,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是(
)
A.4
B.8
C.12
D.16
2.根据尺规作图的痕迹,可以判定点O为的内心的是(
)
A.B.C.
D.
3.如图,在中,是外一点,与相切于两点,是上两点,若,则(
)
A.210°
B.215°
C.220°
D.225°
4.如图PA、PB是圆O的切线,切点分别为A、B,点C在AB上,过C作圆O的切线分别交PA、PB于点D、E,连接OD、OE,若∠P=50°,则∠DOE的度数为( )
A.130°
B.50°
C.60°
D.65°
5.在中,,则这个三角形的外接圆和内切圆半径分别是(
)
A.
B.
C.
D.
6.如图,点为的内心,,,点,分别为,上的点,且.
甲、乙、丙三人有如下判断:
甲:;
乙:四边形的面积是定值;
丙:当时,的周长取得最小值.
则下列说法正确的是(
)
A.只有甲正确
B.只有丙错误
C.乙、丙都正确
D.甲、乙、丙都正确
二.填空题
7.PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=50°,则∠COD的度数为____.
8.如图,在中,,I是内心,O是外心,则__________.
三.解答题
9.如图,AB,BC,CD分别与⊙O相切于E,F,G三点,且AB//CD,BO=6cm,CO=8cm.求BC的长及⊙O的半径.
10.已知如图,中,内切圆的半径.求:的最小值.
11.如图,ABC中,∠ACB=90°,点O在边AC上,经过点C的⊙O与斜边AB相切于点D,交AC边于点E.
(1)求证:∠ACD=∠B;
(2)若BC=6,AC=8,求AD、CD的长.
12.如图,四边形ABCD是平行四边形,点A,B,D均在圆上.请仅用无刻度的直尺分别下列要求画图.
(1)在图①中,若AB是直径,CD与圆相切,画出圆心;
(2)在图②中,若CB,CD均与圆相切,画出圆心.
试卷第2页,总3页
参考答案
1.B
【分析】
根据切线长定理即可得结论.
【详解】
解:∵PA、PB切⊙O于点A、B,
∴PB=PA=4,
∵CD切⊙O于点E,交PA、PB于C、D两点,
∴CA=CE,DB=DE,
∴PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=4+4=8.
则△PCD的周长是8.
故选:B.
【点睛】
本题考查了切线长定理,解决本题的关键是掌握切线的性质.
2.C
【分析】
根据三角形的内心定义和基本尺规作图进行判断即可.
【详解】
解:由于三角形的内心是三角形角平分线的交点,由基本作图知选项C中尺规作图作的是 的平分线,所以点O为的内心,
故选:C.
【点睛】
本题考查基本作图、三角形内心定义,熟练掌握基本尺规作图是解答的关键.
3.B
【分析】
连接AB,根据圆内接四边形性质和切线长定理求出和的度数即可.
【详解】
解:连接AB,
∵与相切于两点,
∴,
∵,
∴,
∵是上两点,
∴,
∴;
故选:B.
【点睛】
本题考查了切线长定理、圆内接四边形性质、等腰三角形性质,解题关键是恰当连接辅助线,构造等腰三角形和圆内接四边形.
4.D
【分析】
连接OA、OB、OC,由切线性质得OB⊥PB、OA⊥PA,从而求得∠AOB的度数,再由切线长定理得到DB=DC,从而证得OD平分∠BOC,同理得OE平分∠AOC,最后由∠DOE=∠AOB得到∠DOE的度数.
【详解】
解:如下图
连OA、OB、OC
∵PB切⊙O于B,PA切⊙O于A
∴OB⊥PB,OA⊥PA
又∠P=50°
∴∠AOB=130°
∵DB切⊙O于B,DE切⊙O于C
∴DB=DC且OC⊥DC
∴OD平分∠BOC,即∠DOC=∠BOC
同理得∠EOC=∠AOC
∴∠DOE=∠DOC+∠EOC
=∠BOC+∠AOC
=(∠BOC+∠AOC)
=∠AOB=×130°
=65°.
故选:D.
【点睛】
此题考查切线的性质、切线长定理,发现∠DOE=∠AOB是关键.
5.C
【分析】
首先根据勾股定理逆定理判断△ABC是直角三角形,得其斜边是10,即可求得外接圆半径和内切圆半径.
【详解】
∵AC=6,BC=8,AC=10,,
∴,
∴△ABC是直角三角形,且斜边是AC=10,
∴其外接圆的半径为5,
三角形的内切圆半径=,
故选:C.
【点睛】
本题考查了三角形的外接圆和内切圆,勾股定理的逆定理;解题的关键是灵活运用勾股定理的逆定理判断△ABC是以AC为斜边的直角三角形.
6.B
【分析】
点为的内心,可用角平分线的性质,再用三角形全等可判断甲和乙,当最小,即当时,的周长最小即可判断丙.
【详解】
(1)∵点为的内心,
∴当于,于时,.
当,不垂直于,时,
如图1,过点作于,于.
则.
∵,
∴.∵,
∴.
∵点为的内心,,,
∴.
∴≌.
∴.故甲的判断正确.
(2)如图1,连接.
由(1)可知,四边形的面积为.
∵点的位置固定,
∴四边形的面积是定值.故乙的判断正确.
(3)如图2,过点作于点.
由(1)可得,.
∴的周长.
∴当最小,即当时,的周长最小,此时不垂直于,故丙的判断不正确.
综上所述,答案选B.
【点睛】
此题考查的是三角形的内心,熟悉掌握三角形内心的性质是解题的关键.
7.65°或115°
【分析】
根据题意画出符合题意的图形,分别求出∠AOB,再根据切线的性质求出∠COD的度数.
【详解】
如图,连接OA、OB、OE
∵PA,PB是⊙O的切线
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°
∵∠APB=50°,
∴∠AOB=360°-90°-90°-50°=130°
∵CD是⊙O的切线
∴OE⊥CD
∵∠CEO=∠DEO=90°
∵PA,PB,CD是⊙O的切线,A,B,E是切点,
∴∠OCA=∠OCE,∠ODB=∠ODE,
∵∠AOC=180°-∠OAC-∠OCA,∠EOC=180°-∠OEC-∠OCE,
∴∠AOC=∠EOC
同理可得∠BOD=∠EOD
∴∠COD=∠EOC+∠EOD=∠AOE+∠BOE=∠AOB=65°
如图,连接OA、OB、OE
同理可得∠AOB=130°
同理可得∠COD=∠EOC+∠EOD=∠AOE+∠BOE
∴∠COD=(360°-130°)=115°
故答案为:65°或115°.
【点睛】
此题主要考查考查了切线的性质,切线长定理,三角形的内角和等知识点的应用,解题的关键是根据题意分情况作图求解.
8.140°
【分析】
根据三角形的内心得出,根据三角形内角和定理求出,进而可求得的度数,根据圆周角定理即可求得∠BOC.
【详解】
解:在△ABC中,∠BIC=125°,I是内心,
∴,
∴,
∴
∴,
∵O是外心,
∴,
故答案为:140°.
【点睛】
本题考查了三角形的内切圆和三角形的外接圆,圆周角定理,三角形的内角和定理等知识点.正确识别图中相关角是解题关键.
9.BC=10cm,半径为cm.
【分析】
由切线长定理和可证明是直角三角形,在Rt
中,由勾股定理可求得BC长.连接OF,利用等积法可求得OF的长,OF即为半径长.
【详解】
(1)∵AB、BC、CD是的切线
∴BF=BE,CF=CG,∠OBC=∠ABC,∠BCO=∠BCD
∵
∴∠ABC+∠BCD=
∴∠OBC+∠BCO=
∴∠BOC=
∴是直角三角形
∵BO=6,CO=8
∴
∴BC的长为10cm.
(2)连接OF,
∵BC与相切与点F
∴
利用面积可得:
∴
∴的半径为cm.
【点睛】
本题主要考察切线长定理,求得是直角是解题的关键.
10.最小值是.
【分析】
根据Rt△ABC中,内切圆O的半径r,三角形三个边分别为:a、b、c,可得S△ABC=ab,ab=2S△,2r=a+b c,c=a+b 2r,再根据勾股定理列出方程,根据一元二次方程根的判别式即可求解.
【详解】
解:∵中,内切圆的半径,三角形三个边分别为:、、,
∴.
设,
∴.
∵,
∴.
∴.
两边平方,得,
.
将,代入,得:
,.
∵且,
∴,是方程的两个根.
∵,是正实数,
∴△,即.
.
解得或,不合题意舍去.
∴的最小值是.
【点睛】
本题考查了三角形的内切圆与内心的应用,解决本题的关键是综合运用三角形内切圆的性质、一元二次方程根的判别式等知识.
11.(1)见解析;(2)4,
【分析】
(1)连接OD,如图,根据切线的性质得到∠ODB=90°,∠ABC+∠COD=180°,再根据等角的补角得到∠AOD=∠ABC,然后根据圆周角定理得到∠AOD=2∠ACD,从而得到结论;
(2)先利用勾股定理计算出在AB=10,再利用切线长定理得到BD=BC=6,利用线段差可得AD=4,设⊙O的半径为r,则OD=OC=r,OA=8﹣r,利用勾股定理得到r2+42=(8﹣r)2,解得r=3,连接OB交CD于H,如图,则OB垂直平分CD,然后利用面积法可计算出CH,从而得到CD的长.
【详解】
(1)证明:连接OD,如图,
∵AB为切线,
∴OD⊥AB,
∴∠ODB=90°,
∵∠ACB=90°,
∴∠ABC+∠COD=180°,
∵∠AOD+∠COD=180°,
∴∠AOD=∠ABC,
∵OD=OC,
∴∠OCD=∠ODC,
∵∠AOD=∠OCD+∠ODC
=2∠ACD,
∴∠ACD=∠ABC;
(2)解:在Rt△ABC中,AB==10,
∵OC⊥CB,OC为半径,
∴BC为切线,
∴BD=BC=6,
∴AD=4,
设⊙O的半径为r,则OD=OC=r,OA=8﹣r,
在Rt△AOD中,r2+42=(8﹣r)2,
解得r=3,
∴OC=3,
连接OB交CD于H,如图,
∵OC=OD,BC=BD,
∴OB垂直平分CD,
在Rt△OCB中,OB=,
∵OB CH=OC BC,
∴CH=,
∴CD=2CH=.
【点睛】
本题考查切线性质,四边形内角和,等角的补角性质,圆周角定理,等腰三角形性质,外角性质,勾股定理,切线长定理,三角形面积掌握并会利用这些知识是解题关键.
12.(1)见解析;(2)见解析
【分析】
(1)延长CB交圆于一点,把这点与点D连接,与AB交点即为圆心;
(2)连接AC、BD交于点G,AC交圆于点E,射线DE交BC于F,射线FG交DA于H,连接BH交AC于O即可.
【详解】
(1)如图1所示,延长CB交圆于点E,连接DE,与AB交点即为圆心;
由已知可得∠A+∠DBA=90°,∠EBA=∠C=∠A,故∠EBA
+∠DBA=90°,DE为直径;
(2)如图2所示,连接AC、BD交于点G,AC交圆于点E,射线DE交BC于F,射线FG交DA于H,连接BH交AC于O.点即为所求.说明:由已知可得,△ADB为等边三角形,由作图可知,AE为直径,DF⊥BC,可得,F是BC中点,进而得出H是AD中点,BH⊥AD,BH过圆心;
【点睛】
本题考查了无刻度直尺作图,解题关键是准确理解题意,根据圆的有关性质进行作图.
答案第12页,总12页
同课章节目录
