1.5 三角函数的应用 课件-2021-2022学年北师版数学九年级下册(共24张PPT)
文档属性
| 名称 | 1.5 三角函数的应用 课件-2021-2022学年北师版数学九年级下册(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 08:06:22 | ||
图片预览








文档简介
(共24张PPT)
1.5
三角函数的应用
第1章
直角三角形的边角关系
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
利用解直角三角形的知识解一般实际应用问题
课时导入
回顾与思考
1.解直角三角形的意义:在直角三角形中,由已知元素
求出所有未知元素的过程,叫做直角三角形.
2.直角三角形中诸元素之间的关系:
(1)三边之间的关系:a2+b2=c2
(勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
把∠A换成∠B同样适用.
利用解直角三角形的知识解一般实际应用问题
知1-讲
感悟新知
想一想
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测
得仰角为30°,再往塔的方向前
进50m至B处,测得仰角
为60°,那么该塔有多
高?
(小明的身高忽略不计,结
果精确到1m)
类型1
借助工具测量的应用
知识点
利用解直角三角形的知识解一般实际应用问题
1
感悟新知
知1-讲
1.运用锐角三角函数解决实际问题的方法:
(1)弄清题意,画出示意图;
(2)找出图形中的线段、角所表示的实际意义,并找到所要
解决的问题;
(3)寻找要求解的直角三角形,有时需要作适当的辅助线;
(4)选择合适的边角关系式,进行有关锐角三角函数的计算;
(5)按照题目要求的精确度确定答案,并注明单位,作答.
感悟新知
知1-练
中国益阳”网上消息,益阳市为了改善市区交通
状况,计划在康富路的北端修建通往资江北岸的新大桥.
如图,新大桥的两端位于A,B两点,小张为了测量A,B
之间的河宽,在垂直于新大桥AB的直线形道路l上测得如下
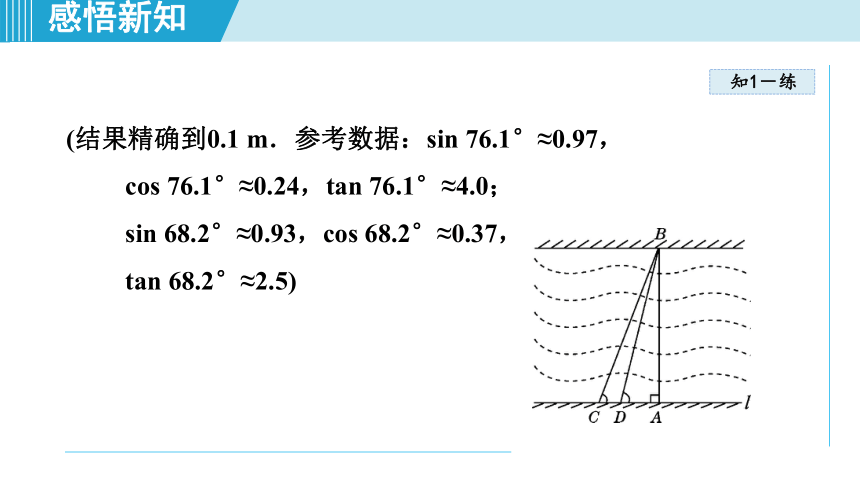
数据:∠BDA=76.1°,∠BCA=68.2°,CD=82
m.求
AB的长.
例
1
知1-练
感悟新知
(结果精确到0.1
m.参考数据:sin
76.1°≈0.97,
cos
76.1°≈0.24,tan
76.1°≈4.0;
sin
68.2°≈0.93,cos
68.2°≈0.37,
tan
68.2°≈2.5)
知1-练
感悟新知
导引:设AD=x
m,在Rt△ABC中,利用∠BCA的正切值,
可以用含x的代数式表示AB.同理在Rt△ABD中,利
用∠BDA的正切值表示出AB,从而列出关于x的方程,
求出x的值就能求出AB的长了.
知1-练
感悟新知
设AD=x
m,则AC=(x+82)
m.
在Rt△ABC中,tan
∠BCA=
∴AB=AC·tan
∠BCA=(x+82)tan
68.2°
m.
在Rt△ABD中,tan
∠BDA=
∴AB=AD·tan
∠BDA=xtan
76.1°
m.
∴(x+82)tan
68.2°=xtan
76.1°.∴x≈136.67.
∴AB≈4×136.67≈546.7(m).即AB的长约为546.7
m.
解:
知1-练
感悟新知
1.
如图,AB是斜靠在墙上的长梯,D是梯上一点,梯
脚B与墙脚的距离为1.6
m(即BC的长),点D与墙的距离为1.4
m(即DE的长),BD长为0.55
m,则梯子的长为( )
A.4.50
m
B.4.40
m
C.4.00
m
D.3.85
m
B
知1-练
感悟新知
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1
m,则旗杆PA的高度为( )
B.
C.
D.
2.
A
知1-讲
感悟新知
3.
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
A.5sin
36°米
B.5cos
36°米
C.5tan
36°米
D.10tan
36°米
C
知1-练
感悟新知
如图
1-5-5,某居民楼Ⅰ高
20
m,窗户朝南,该楼内一
楼住户的窗台离地面的距离
CM
为
2
m,窗户
CD
高
1.8
m.
现计划在楼Ⅰ的正南方距楼Ⅰ
30
m
处新建一居民楼Ⅱ
.
当正午时刻太阳光线与地面成
30°角时,要使楼Ⅱ的影子不影响楼Ⅰ所有住户的采光,新建楼Ⅱ最高只能建多少米?
类型2
借助影子测量的应用
例2
知1-练
感悟新知
设正午时刻太阳光线正好照在楼Ⅰ
一楼的窗台处,此时新建居民楼Ⅱ高
EG=x
m,如图
1-5-5,过
C
作
CF
⊥
EG
于
F,则
FG=CM=2
m.
在
Rt
△
ECF
中,
EF=(
x-2)
m,
FC=30
m,∠ECF=30°,
即新建楼Ⅱ
最高只能建
解:
知2-练
感悟新知
解法提醒:
解本题的关键是将实际中的相关数据,通过建立数学模型,归结到直角三角形中,再用三角函数(
正切)
求解.注:本题也可以用30°角的直角三角形的三边关系,建立方程求解.
知1-练
感悟新知
1.
如图,AB是伸缩式遮阳棚,CD是窗户,要想在夏
至的正午时刻阳光刚好不能射入窗户,则AB的长
是________米.(假设夏
至的正午时刻阳光与地
平面的夹角为60°)
知1-练
感悟新知
2.
如图,已知电线杆AB直立于地面上,它的影子恰好
照在土坡的坡面CD和地面BC上,如果CD与地面成
45°,∠A=60°,CD=4
m,BC=(4
-2
)
m,则电线杆AB的长为________.
知1-练
感悟新知
如图,要在宽为22
m的九州大道两边安装路灯,路灯的灯臂CD长2
m,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A.(11-2
)
m
B.(11
-2
)
m
C.(11-2
)
m
D.(11
-4)
m
3.
D
课堂小结
三角函数的应用
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
课堂小结
(3)得到数学问题的答案;
(4)得到实际问题的答案.
三角函数的应用
课堂小结
如图,某海岛上的观察所A发现海上某船只B,并测得其俯角α=
8°35′
.已知观察所
A
的标高(当水位为
0
m时的高度)
为45.54
m,当时水位为+2.34
m.求观察所A与船只B的水平距离(结果保留整数,参考数据:sin8°35′≈0.149,cos
8°35′
≈0.989,tan
8°35′≈0.151).
三角函数的应用
课堂小结
易错点:忽略求正切值的前提.
三角函数的应用
课堂小结
由题意可知AC=45.54-2.34=43.2(m).
在Rt△ABC中,∠ABC=α=8°35′,
tan
∠ABC=
∴BC=
因此观察所A与船只B的水平距离约为286
m.
解:
三角函数的应用
课堂小结
易错总结:解题时容易弄错AC的高度,A处的标高为45.54
m(水位为0
m时的高度),当水位为+2.34
m时,即水位上升了2.34
m,则AC的高度为45.54-2.34=43.2(m).
三角函数的应用
1.5
三角函数的应用
第1章
直角三角形的边角关系
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
利用解直角三角形的知识解一般实际应用问题
课时导入
回顾与思考
1.解直角三角形的意义:在直角三角形中,由已知元素
求出所有未知元素的过程,叫做直角三角形.
2.直角三角形中诸元素之间的关系:
(1)三边之间的关系:a2+b2=c2
(勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
把∠A换成∠B同样适用.
利用解直角三角形的知识解一般实际应用问题
知1-讲
感悟新知
想一想
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测
得仰角为30°,再往塔的方向前
进50m至B处,测得仰角
为60°,那么该塔有多
高?
(小明的身高忽略不计,结
果精确到1m)
类型1
借助工具测量的应用
知识点
利用解直角三角形的知识解一般实际应用问题
1
感悟新知
知1-讲
1.运用锐角三角函数解决实际问题的方法:
(1)弄清题意,画出示意图;
(2)找出图形中的线段、角所表示的实际意义,并找到所要
解决的问题;
(3)寻找要求解的直角三角形,有时需要作适当的辅助线;
(4)选择合适的边角关系式,进行有关锐角三角函数的计算;
(5)按照题目要求的精确度确定答案,并注明单位,作答.
感悟新知
知1-练
中国益阳”网上消息,益阳市为了改善市区交通
状况,计划在康富路的北端修建通往资江北岸的新大桥.
如图,新大桥的两端位于A,B两点,小张为了测量A,B
之间的河宽,在垂直于新大桥AB的直线形道路l上测得如下
数据:∠BDA=76.1°,∠BCA=68.2°,CD=82
m.求
AB的长.
例
1
知1-练
感悟新知
(结果精确到0.1
m.参考数据:sin
76.1°≈0.97,
cos
76.1°≈0.24,tan
76.1°≈4.0;
sin
68.2°≈0.93,cos
68.2°≈0.37,
tan
68.2°≈2.5)
知1-练
感悟新知
导引:设AD=x
m,在Rt△ABC中,利用∠BCA的正切值,
可以用含x的代数式表示AB.同理在Rt△ABD中,利
用∠BDA的正切值表示出AB,从而列出关于x的方程,
求出x的值就能求出AB的长了.
知1-练
感悟新知
设AD=x
m,则AC=(x+82)
m.
在Rt△ABC中,tan
∠BCA=
∴AB=AC·tan
∠BCA=(x+82)tan
68.2°
m.
在Rt△ABD中,tan
∠BDA=
∴AB=AD·tan
∠BDA=xtan
76.1°
m.
∴(x+82)tan
68.2°=xtan
76.1°.∴x≈136.67.
∴AB≈4×136.67≈546.7(m).即AB的长约为546.7
m.
解:
知1-练
感悟新知
1.
如图,AB是斜靠在墙上的长梯,D是梯上一点,梯
脚B与墙脚的距离为1.6
m(即BC的长),点D与墙的距离为1.4
m(即DE的长),BD长为0.55
m,则梯子的长为( )
A.4.50
m
B.4.40
m
C.4.00
m
D.3.85
m
B
知1-练
感悟新知
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1
m,则旗杆PA的高度为( )
B.
C.
D.
2.
A
知1-讲
感悟新知
3.
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
A.5sin
36°米
B.5cos
36°米
C.5tan
36°米
D.10tan
36°米
C
知1-练
感悟新知
如图
1-5-5,某居民楼Ⅰ高
20
m,窗户朝南,该楼内一
楼住户的窗台离地面的距离
CM
为
2
m,窗户
CD
高
1.8
m.
现计划在楼Ⅰ的正南方距楼Ⅰ
30
m
处新建一居民楼Ⅱ
.
当正午时刻太阳光线与地面成
30°角时,要使楼Ⅱ的影子不影响楼Ⅰ所有住户的采光,新建楼Ⅱ最高只能建多少米?
类型2
借助影子测量的应用
例2
知1-练
感悟新知
设正午时刻太阳光线正好照在楼Ⅰ
一楼的窗台处,此时新建居民楼Ⅱ高
EG=x
m,如图
1-5-5,过
C
作
CF
⊥
EG
于
F,则
FG=CM=2
m.
在
Rt
△
ECF
中,
EF=(
x-2)
m,
FC=30
m,∠ECF=30°,
即新建楼Ⅱ
最高只能建
解:
知2-练
感悟新知
解法提醒:
解本题的关键是将实际中的相关数据,通过建立数学模型,归结到直角三角形中,再用三角函数(
正切)
求解.注:本题也可以用30°角的直角三角形的三边关系,建立方程求解.
知1-练
感悟新知
1.
如图,AB是伸缩式遮阳棚,CD是窗户,要想在夏
至的正午时刻阳光刚好不能射入窗户,则AB的长
是________米.(假设夏
至的正午时刻阳光与地
平面的夹角为60°)
知1-练
感悟新知
2.
如图,已知电线杆AB直立于地面上,它的影子恰好
照在土坡的坡面CD和地面BC上,如果CD与地面成
45°,∠A=60°,CD=4
m,BC=(4
-2
)
m,则电线杆AB的长为________.
知1-练
感悟新知
如图,要在宽为22
m的九州大道两边安装路灯,路灯的灯臂CD长2
m,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A.(11-2
)
m
B.(11
-2
)
m
C.(11-2
)
m
D.(11
-4)
m
3.
D
课堂小结
三角函数的应用
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
课堂小结
(3)得到数学问题的答案;
(4)得到实际问题的答案.
三角函数的应用
课堂小结
如图,某海岛上的观察所A发现海上某船只B,并测得其俯角α=
8°35′
.已知观察所
A
的标高(当水位为
0
m时的高度)
为45.54
m,当时水位为+2.34
m.求观察所A与船只B的水平距离(结果保留整数,参考数据:sin8°35′≈0.149,cos
8°35′
≈0.989,tan
8°35′≈0.151).
三角函数的应用
课堂小结
易错点:忽略求正切值的前提.
三角函数的应用
课堂小结
由题意可知AC=45.54-2.34=43.2(m).
在Rt△ABC中,∠ABC=α=8°35′,
tan
∠ABC=
∴BC=
因此观察所A与船只B的水平距离约为286
m.
解:
三角函数的应用
课堂小结
易错总结:解题时容易弄错AC的高度,A处的标高为45.54
m(水位为0
m时的高度),当水位为+2.34
m时,即水位上升了2.34
m,则AC的高度为45.54-2.34=43.2(m).
三角函数的应用
