苏科版八年级数学上册 2.5 等腰三角形的轴对称性(共11张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 2.5 等腰三角形的轴对称性(共11张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 09:59:48 | ||
图片预览


文档简介
(共11张PPT)
2.5 等腰三角形的轴对称性
A
B
C
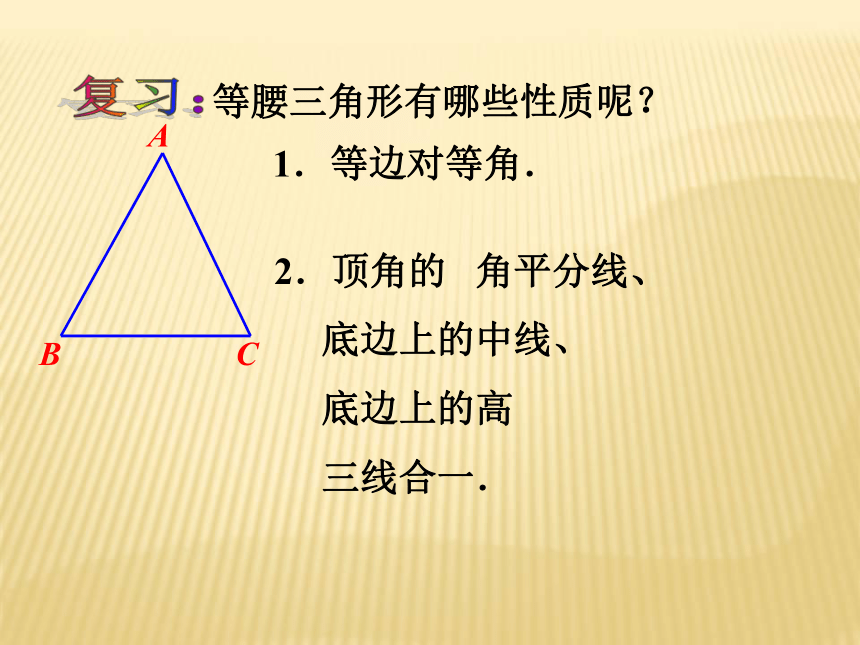
1.等边对等角.
等腰三角形有哪些性质呢?
2.顶角的
角平分线、
底边上的中线、
底边上的高
三线合一.
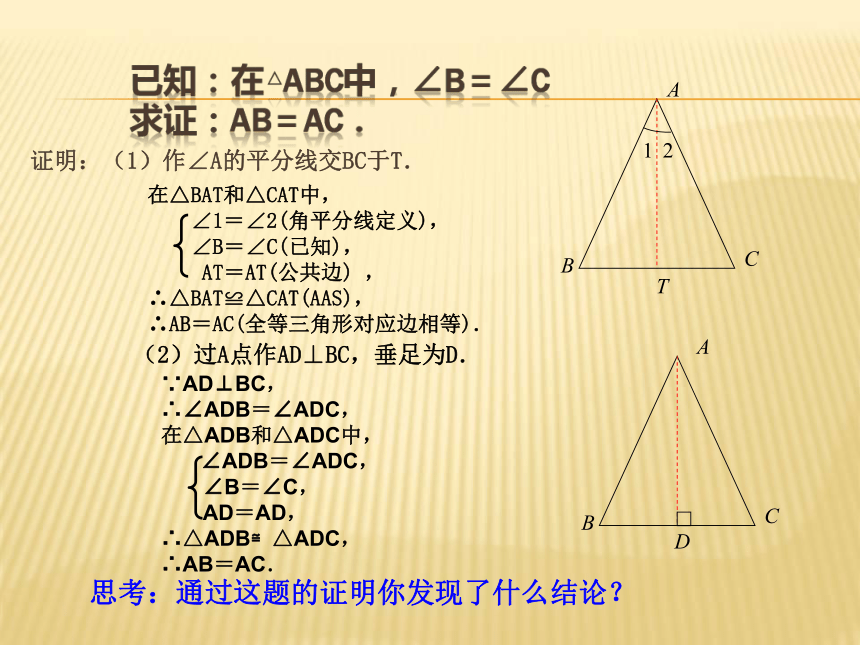
在△BAT和△CAT中,
∠1=∠2(角平分线定义),
∠B=∠C(已知),
AT=AT(公共边)
,
∴△BAT≌△CAT(AAS),
∴AB=AC(全等三角形对应边相等).
证明:(1)作∠A的平分线交BC于T.
A
B
C
T
(2)过A点作AD⊥BC,垂足为D.
A
B
C
D
∵AD⊥BC,
∴∠ADB=∠ADC,
在△ADB和△ADC中,
∠ADB=∠ADC,
∠B=∠C,
AD=AD,
∴△ADB≌△ADC,
∴AB=AC.
思考:通过这题的证明你发现了什么结论?
1
2
符号语言
图形
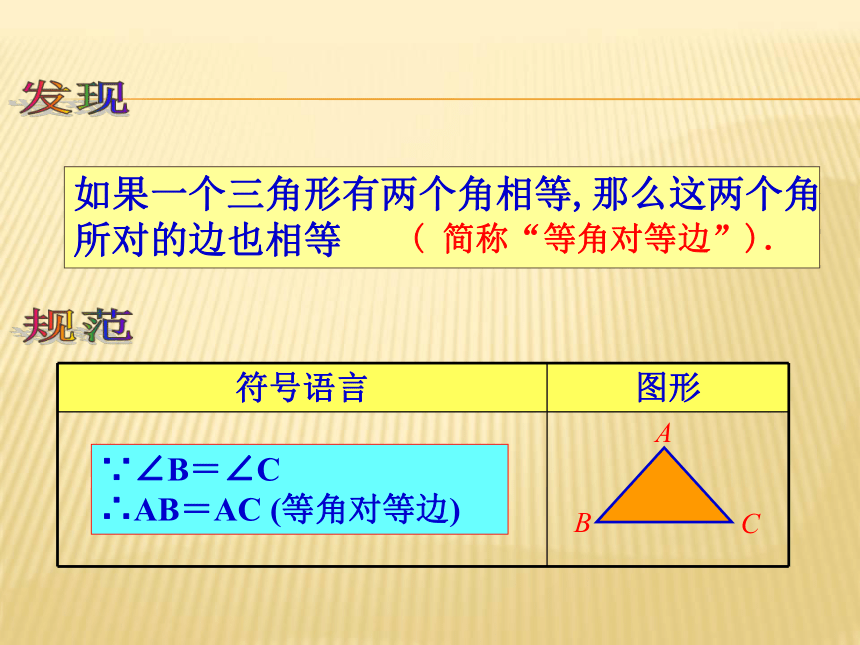
如果一个三角形有两个角相等,那么这两个角
所对的边也相等
(
简称“等角对等边”).
∵∠B=∠C
∴AB=AC
(等角对等边)
A
B
C
请思考:
“等边对等角”与“等角对等边”
是否一样?它们的主要区别在哪里?
(它们的条件与结论正好调换了过来,
这也叫互逆命题).
例题讲评:
如图,在
⊿ABC中,AB=AC,角平分线BD、CE相交于点O,
求证:OB=OC
A
E
B
C
D
O
变式引申:连接DE,AD=AE吗?
应用:
1.⊿ABC中,
∠B=
∠C,AD⊥BC,DE∥AB。
求证:⊿ADE是等腰三角形
A
B
D
C
E
2.在⊿ABC中,∠ABC、
∠ACB
的平分线交于点O,过点O作DE∥BC分别交AB、AC于点D、E。
求证:DE=BD+EC。
A
B
C
E
D
O
探索:
如图所示进行折叠
A
B
C
E
D
F
最后展开后,
∠A=
,∠B=
。
由此可得到
=
,
=
。
你可以得到什么结论?
∠ACD
∠BCD
DA
DC
DB
DC
直角三角形斜边上的中线等于斜边的一半
应用:
如图,在直角⊿ABC中,CD是斜边AB上的中线,DE⊥AC,垂足为E。
(1)如果CD=2.4cm,那么AB=
;
(2)写出图中相等的线段和角。
A
B
D
C
E
4.8cm
回头一看,我想说……
通过本节课的学习:
(1)你有哪些收获?
(2)你还有什么疑惑?
2.5 等腰三角形的轴对称性
A
B
C
1.等边对等角.
等腰三角形有哪些性质呢?
2.顶角的
角平分线、
底边上的中线、
底边上的高
三线合一.
在△BAT和△CAT中,
∠1=∠2(角平分线定义),
∠B=∠C(已知),
AT=AT(公共边)
,
∴△BAT≌△CAT(AAS),
∴AB=AC(全等三角形对应边相等).
证明:(1)作∠A的平分线交BC于T.
A
B
C
T
(2)过A点作AD⊥BC,垂足为D.
A
B
C
D
∵AD⊥BC,
∴∠ADB=∠ADC,
在△ADB和△ADC中,
∠ADB=∠ADC,
∠B=∠C,
AD=AD,
∴△ADB≌△ADC,
∴AB=AC.
思考:通过这题的证明你发现了什么结论?
1
2
符号语言
图形
如果一个三角形有两个角相等,那么这两个角
所对的边也相等
(
简称“等角对等边”).
∵∠B=∠C
∴AB=AC
(等角对等边)
A
B
C
请思考:
“等边对等角”与“等角对等边”
是否一样?它们的主要区别在哪里?
(它们的条件与结论正好调换了过来,
这也叫互逆命题).
例题讲评:
如图,在
⊿ABC中,AB=AC,角平分线BD、CE相交于点O,
求证:OB=OC
A
E
B
C
D
O
变式引申:连接DE,AD=AE吗?
应用:
1.⊿ABC中,
∠B=
∠C,AD⊥BC,DE∥AB。
求证:⊿ADE是等腰三角形
A
B
D
C
E
2.在⊿ABC中,∠ABC、
∠ACB
的平分线交于点O,过点O作DE∥BC分别交AB、AC于点D、E。
求证:DE=BD+EC。
A
B
C
E
D
O
探索:
如图所示进行折叠
A
B
C
E
D
F
最后展开后,
∠A=
,∠B=
。
由此可得到
=
,
=
。
你可以得到什么结论?
∠ACD
∠BCD
DA
DC
DB
DC
直角三角形斜边上的中线等于斜边的一半
应用:
如图,在直角⊿ABC中,CD是斜边AB上的中线,DE⊥AC,垂足为E。
(1)如果CD=2.4cm,那么AB=
;
(2)写出图中相等的线段和角。
A
B
D
C
E
4.8cm
回头一看,我想说……
通过本节课的学习:
(1)你有哪些收获?
(2)你还有什么疑惑?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
