苏科版八年级数学上册 3.3 勾股定理的简单应用课件(17张)
文档属性
| 名称 | 苏科版八年级数学上册 3.3 勾股定理的简单应用课件(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 12:04:05 | ||
图片预览



文档简介
(共17张PPT)
勾股定理的应用㈠
3
4
“路”
A
B
C
情景引入
:
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,若在拐角的两边缘走,要分别走3米和4米,那么请同学们计算走“捷径”仅仅少走了________步路,
而踩伤了花草。(假设1米为2步)
5
4
芳草青青,足下留情!
一架长为10m的梯子AB斜靠在墙上.
⑴
若梯子的顶端距地面的垂直距离为8m,则梯子的顶端A与它的底端B哪个距墙角C远
A
B
C
例1
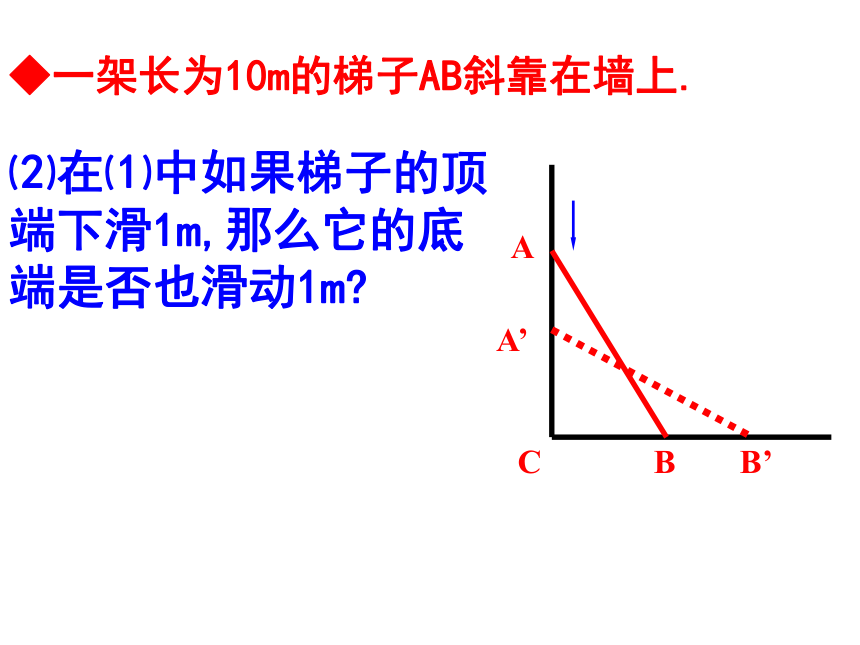
◆一架长为10m的梯子AB斜靠在墙上.
A
B
C
A’
B’
⑵在⑴中如果梯子的顶端下滑1m,那么它的底端是否也滑动1m
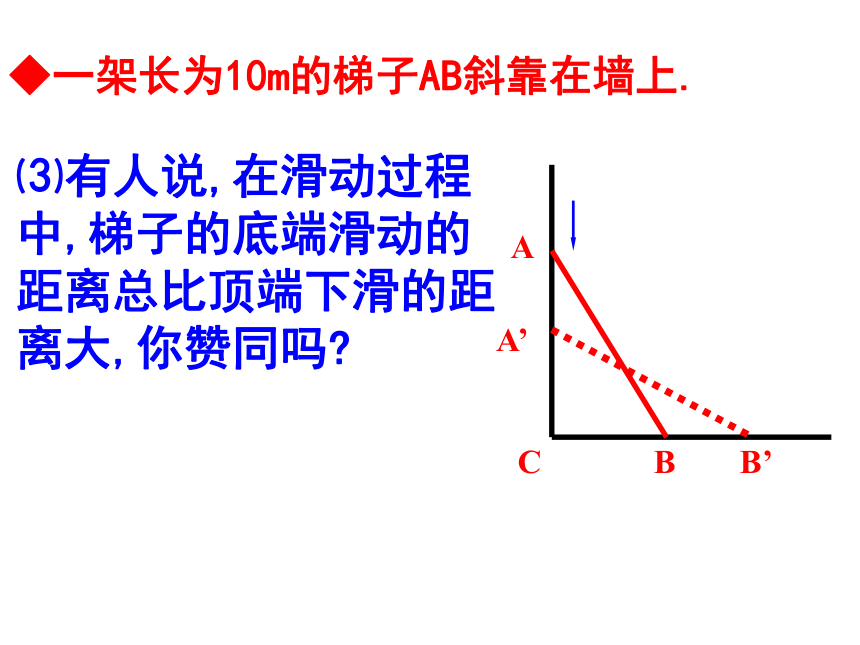
◆一架长为10m的梯子AB斜靠在墙上.
A
B
C
⑶有人说,在滑动过程中,梯子的底端滑动的距离总比顶端下滑的距离大,你赞同吗
A’
B’
图⑴
图⑵
A
B
C
D
E
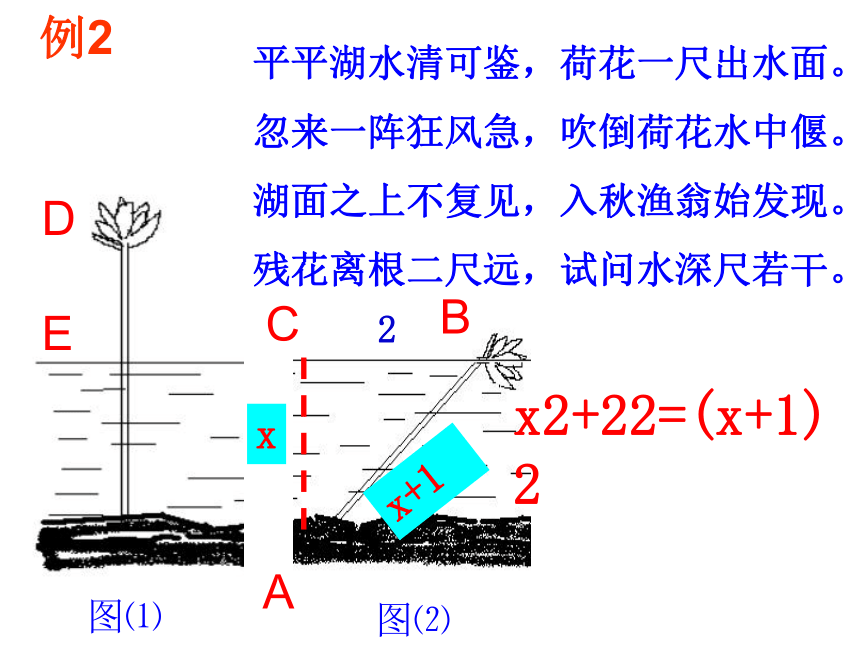
平平湖水清可鉴,荷花一尺出水面。
忽来一阵狂风急,吹倒荷花水中偃。
湖面之上不复见,入秋渔翁始发现。
残花离根二尺远,试问水深尺若干。
x2+22=(x+1)2
2
x
x+1
例2
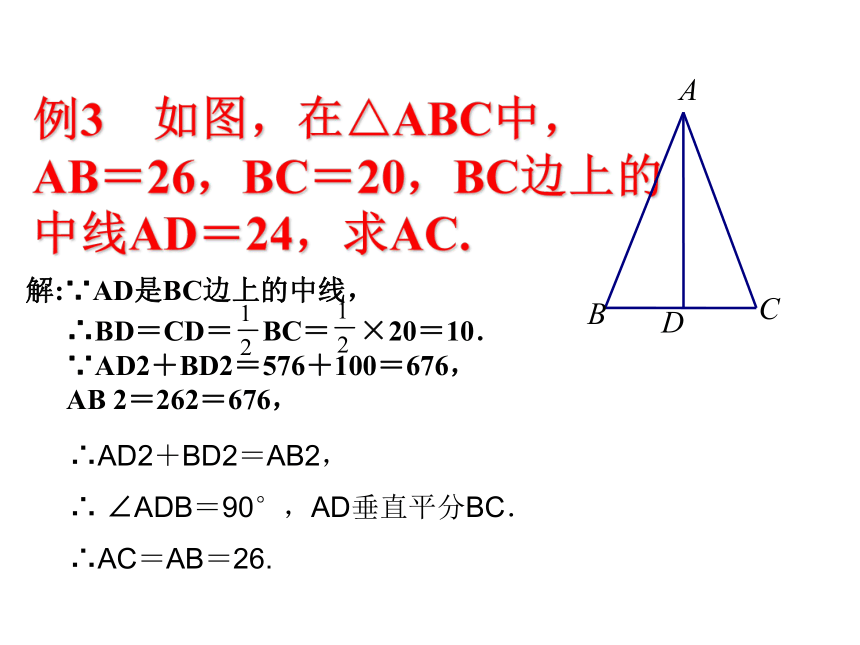
例3 如图,在△ABC中,
AB=26,BC=20,BC边上的
中线AD=24,求AC.
解:∵AD是BC边上的中线,
∴AD2+BD2=AB2,
∴
∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
D
C
B
A
∴BD=CD=
BC=
×20=10.
∵AD2+BD2=576+100=676,
AB
2=262=676,
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状.
1、
如图,盒内长,宽,高分别是4米,3米和12米,盒内可放的棍子最长有多长?
12
4
3
A
B
C
D
E
2.如图是
一大厦的柱子,它是圆柱形的
,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离是多少?(圆周率取3)
A
B
·
A
B
·
8
22×3
6
C
10
教学反思
(1)你认为勾股定理有什么用途?一般如何用
(2)勾股定理与生活实际有什么联系?
1.
如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了
(
)
A.7m
B.8m
C.9m
D.10m
8m
A
B
C
8m
2m
D
A
B
C
2.如图,太阳能热水器的支架AB长为90cm,与AB垂直的BC长120cm.太阳能真空管AC有多长
3.
一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,
问吸管要做多长?
A
B
C
A
B
C
D
O
4.邮递员从车站O正东1km的邮局A出发,先向正北走了3km到B,又向正西走了4km到C,最后再向正南走了6km到D,那么最终该邮递员与邮局的距离为多少km?
1.如图,将长为10米的梯子AC斜靠
在墙上,BC长为6米.
A
B
C
10
6
(1)求梯子上端A到墙的底端B的距离AB。
(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
A1
C1
2
【作业】:
A
B
C
D
2.在Rt△ABC中,∠ACB=90°,AC=4,BC=3.
求Rt△ABC斜边上的中线.
勾股定理的应用㈠
3
4
“路”
A
B
C
情景引入
:
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,若在拐角的两边缘走,要分别走3米和4米,那么请同学们计算走“捷径”仅仅少走了________步路,
而踩伤了花草。(假设1米为2步)
5
4
芳草青青,足下留情!
一架长为10m的梯子AB斜靠在墙上.
⑴
若梯子的顶端距地面的垂直距离为8m,则梯子的顶端A与它的底端B哪个距墙角C远
A
B
C
例1
◆一架长为10m的梯子AB斜靠在墙上.
A
B
C
A’
B’
⑵在⑴中如果梯子的顶端下滑1m,那么它的底端是否也滑动1m
◆一架长为10m的梯子AB斜靠在墙上.
A
B
C
⑶有人说,在滑动过程中,梯子的底端滑动的距离总比顶端下滑的距离大,你赞同吗
A’
B’
图⑴
图⑵
A
B
C
D
E
平平湖水清可鉴,荷花一尺出水面。
忽来一阵狂风急,吹倒荷花水中偃。
湖面之上不复见,入秋渔翁始发现。
残花离根二尺远,试问水深尺若干。
x2+22=(x+1)2
2
x
x+1
例2
例3 如图,在△ABC中,
AB=26,BC=20,BC边上的
中线AD=24,求AC.
解:∵AD是BC边上的中线,
∴AD2+BD2=AB2,
∴
∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
D
C
B
A
∴BD=CD=
BC=
×20=10.
∵AD2+BD2=576+100=676,
AB
2=262=676,
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状.
1、
如图,盒内长,宽,高分别是4米,3米和12米,盒内可放的棍子最长有多长?
12
4
3
A
B
C
D
E
2.如图是
一大厦的柱子,它是圆柱形的
,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离是多少?(圆周率取3)
A
B
·
A
B
·
8
22×3
6
C
10
教学反思
(1)你认为勾股定理有什么用途?一般如何用
(2)勾股定理与生活实际有什么联系?
1.
如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了
(
)
A.7m
B.8m
C.9m
D.10m
8m
A
B
C
8m
2m
D
A
B
C
2.如图,太阳能热水器的支架AB长为90cm,与AB垂直的BC长120cm.太阳能真空管AC有多长
3.
一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,
问吸管要做多长?
A
B
C
A
B
C
D
O
4.邮递员从车站O正东1km的邮局A出发,先向正北走了3km到B,又向正西走了4km到C,最后再向正南走了6km到D,那么最终该邮递员与邮局的距离为多少km?
1.如图,将长为10米的梯子AC斜靠
在墙上,BC长为6米.
A
B
C
10
6
(1)求梯子上端A到墙的底端B的距离AB。
(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
A1
C1
2
【作业】:
A
B
C
D
2.在Rt△ABC中,∠ACB=90°,AC=4,BC=3.
求Rt△ABC斜边上的中线.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
