苏科版八年级数学上册 6.4 用一次函数解决问题课件(26张ppt)
文档属性
| 名称 | 苏科版八年级数学上册 6.4 用一次函数解决问题课件(26张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 13:24:46 | ||
图片预览




文档简介
(共26张PPT)
——————方案专题
1、已知y1=2x,
y2=x+3
若y1=y2,则x=________
若y1>y2,则x的取值范围是_______
若y13
x>3
x<3
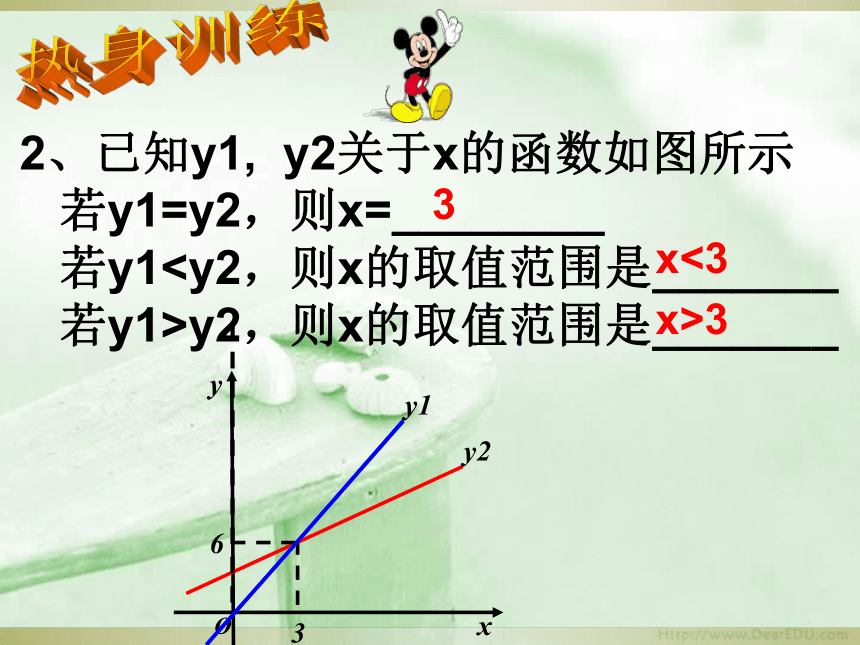
2、已知y1,
y2关于x的函数如图所示
若y1=y2,则x=________
若y1若y1>y2,则x的取值范围是_______
3
x>3
x<3
O
y
3
y1
6
y2
x
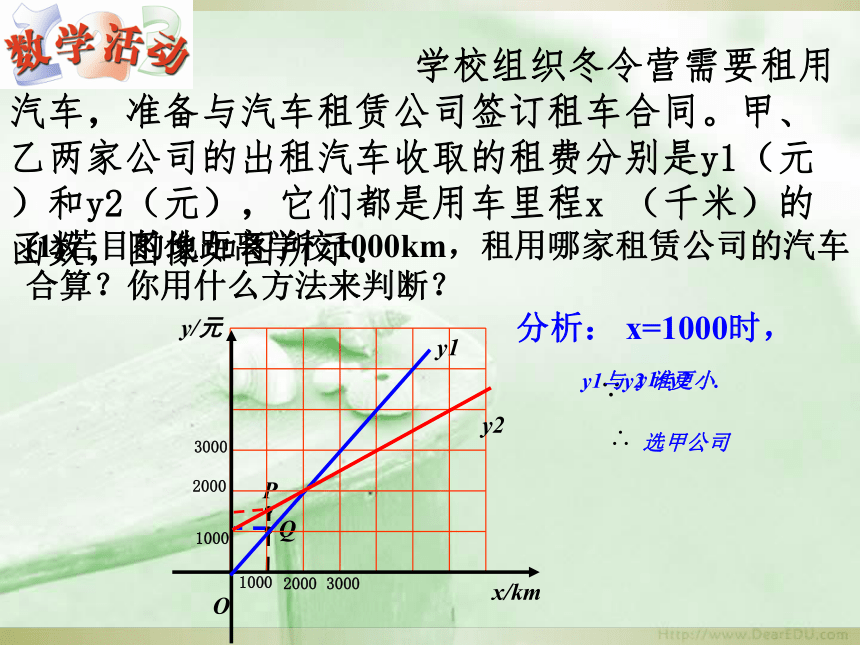
(1)若目的地距离学校1000km,租用哪家租赁公司的汽车合算?你用什么方法来判断?
P
Q
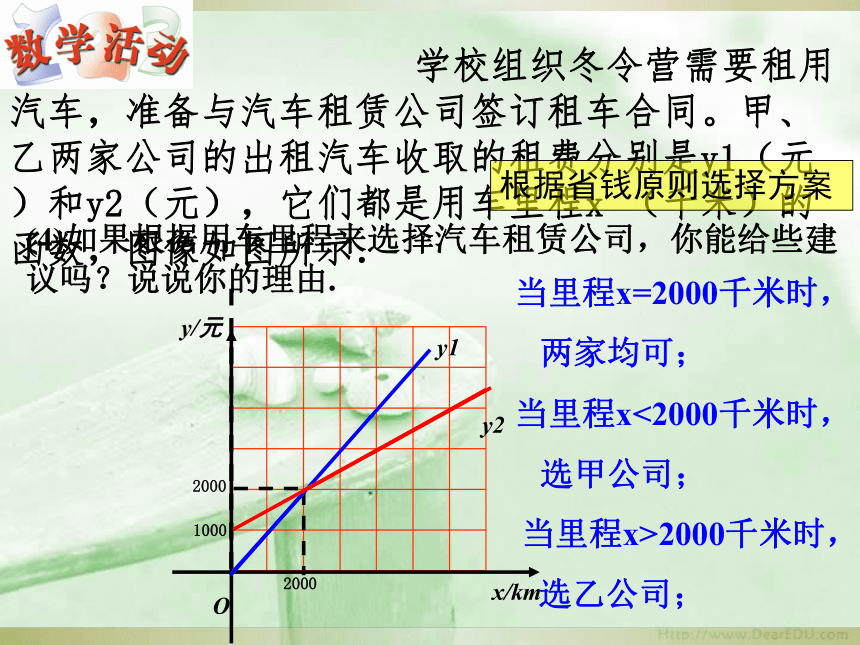
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
1000
y/元
1000
y1
y2
2000
2000
3000
3000
分析:
x=1000时,
x/km
y1选甲公司
y1与y2
谁更小.
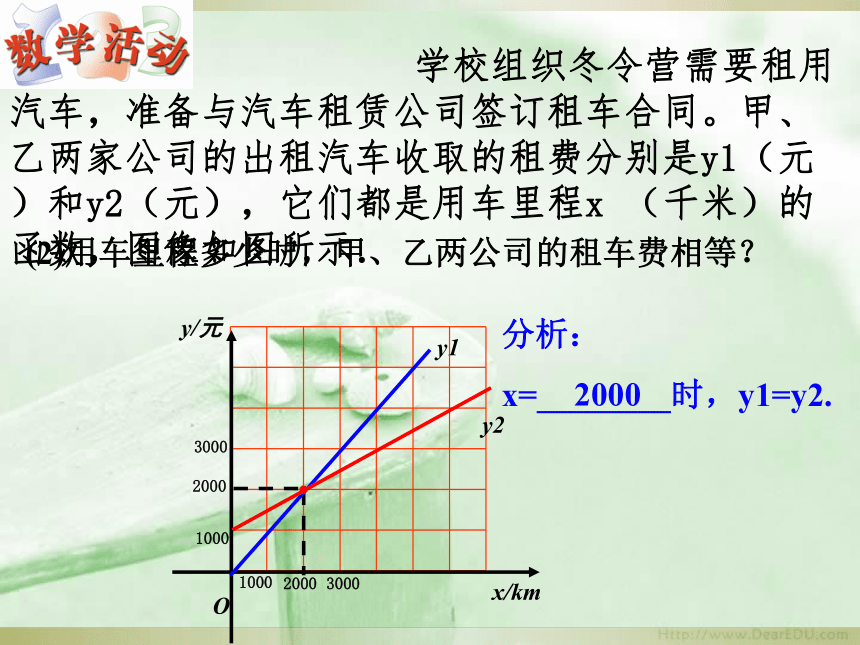
(2)用车里程多少时,甲、乙两公司的租车费相等?
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
1000
x/km
y/元
1000
y1
y2
2000
2000
3000
3000
分析:
x=________时,y1=y2.
2000
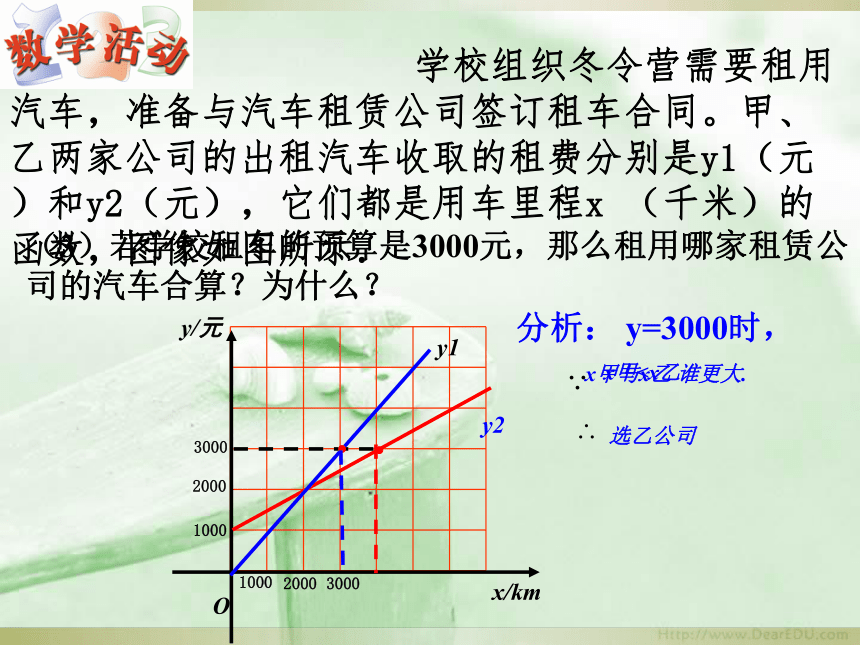
(3)若学校租车的预算是3000元,那么租用哪家租赁公司的汽车合算?为什么?
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
1000
y/元
2000
1000
y1
y2
2000
3000
3000
分析:
y=3000时,
x/km
x甲与x乙
谁更大.
x甲选乙公司
(4)如果根据用车里程来选择汽车租赁公司,你能给些建议吗?说说你的理由.
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
y/元
2000
1000
y1
y2
2000
x/km
当里程x=2000千米时,
两家均可;
当里程x<2000千米时,
选甲公司;
当里程x>2000千米时,
选乙公司;
根据省钱原则选择方案
1.某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示,当租书时间为120天时,应使用
比较合算.
会员卡
试一试
2、如图中,l1反映了某公司产品的销售额与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图象判断该公司盈利时销售量为(
)
(A)小于4件
(B)大于4件
(C)等于4件
(D)大于或等于4件
X(件)
Y(元)
1
2
3
4
5
6
100
200
300
400
500
l1
l2
O
B
交点的意义是什么?
(4)如果根据用车里程来选择汽车租赁公司,你能给些建议吗?说说你的理由.
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
y/元
2000
1000
y1
y2
2000
x/km
O
x/km
y/元
1000
y1
y2
2000
2500
3000
3000
2000
如果根据用车里程来选择汽车租赁公司,你能给些建议吗?说说你的理由.
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
=x
=0.5x+1000
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲汽车出租公司按每100
千米100元收取租车费;乙汽车出租公司按每100千米50元收取租车费,另加管理费800元.如果根据用车路程来选择,试判断租用哪家公司的汽车费用较少?
分析:先确定函数表达式;再求交点
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲汽车出租公司按每100
千米100元收取租车费;乙汽车出租公司按每100千米50元收取租车费,另加管理费1000元.如果根据用车路程来选择,试判断租用哪家公司的汽车费用较少?
解:设用车里程x
(千米)时,甲、乙两家公司收取的租费分别是y1(元)和y2(元)。
则
y1=x
y2=0.5x+1000
O
x/km
y/元
1000
y1=x
y2=0.5x+1000
2000
2000
从“形”上看
x=2000.一样
从“数”上看
(1)
由y1=y2.
得x=
0.5x+1000
,
x<2000.
选甲
(2)
由y1<y2.
得x<0.5x+1000
,
x>2000.选乙
(3)
由y1>y2.
得x>
0.5x+1000
,
甲汽车出租公司按每100千米100元收取租车费;乙汽车出租公司按每100千米50元收取租车费,另加管理费800元.如果根据用车路程来选择,试判断租用哪家公司的汽车费用较少?
1000
x/km
y/元
1000
y1
y2
2000
2000
3000
3000
O
x/km
y/元
1000
y1
2500
3000
3000
y2
(1)确定函数表达式;
(3)“数”的策略:解方程、不等式
(2)求交点;
利用一次函数进行租车等方案选择的一般步骤:
注意:
“形”的策略:画图像,看图说话.
选择方案的依据
A、B两家旅行社分别推出家庭旅游优惠活动,两家旅行社的票价均为90元/人,但优惠办法不同.A旅行社的优惠办法是:全家有一人购全票,其余的人半价优惠;B旅行社的优惠办法是:每人均按三分之二的票价优惠.
y1=90+45(x-1),
解:(1)
y2=60x
(1)请分别写出A、B两旅行社收费y1元、y2元与家庭人数为x人之间的函数表达式.
(2)你将选择哪家旅行社?
即y1=45x+45
y1=45x+45,
解:(1)
y2=60x,
x=3.
由y1=y2.
得45x+45=
60x
,
x>3
由y1<y2.
x<3.
由y1>y2.
法一:(数)
得45x+45<
60x
,
得45x+45>
60x
,
综上,当家庭人数为3人时,两家收费相同,均为180元;
当家庭人数大于3人时,选A旅行社
当家庭人数小于3人时,选B旅行社
(2)
O
y/元
3
y1
y2
180
法二:(形)
45
得交点(3,180).
由.
y=45x+45,
由图可知.
y=60x,
x/人
某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参考数据如下:
(1)请分别写出汽车、火车运输总费用y1(元)、y2(元)与运输路程x(千米)之间的函数表达式.
(2)你认为用哪种运输方式好?
运输方式
速度/(千米/时)
途中综合费用/
(元/时)
装卸费用/(元)
汽车
60
270
200
火车
100
240
410
解:(1)
即y1=4.5x+200
即y2=2.4x+410
O
20
x/千米
y/元
100
200
y1
y2
400
650
运输方式
速度/(千米/时)
途中综合费用/
(元/时)
装卸费用/(元)
汽车
60
270
200
火车
100
240
410
解:(1)
即y1=4.5x+200
即y2=2.4x+410
(2)
得交点(100,650).
由.
y=4.5x+200,
y=2.4x+410,
由图可知.
当运输路程为100千米时,两种运输方式费用相同,均为650元;
当运输路程小于100千米时,选汽车
当运输路程大于100千米时,选火车
下表给出A,B,C
三种上宽带网的收费方式:
收费方式
月使用费/元
包时上网时间/h
超时费/(元/h)
A
30
25
3
B
50
50
3
C
120
不限时
试金石
(1)请分别写出A,B,C
三种方式的月上网费用yA(元)、yB(元)、yC(元)关于每月上网时间t(小时)的函数表达式.
(2)选取哪种方式能节省上网费?
收费方式
月使用费/元
包时上网时间/h
超时费/(元/h)
A
30
25
3
B
50
50
3
C
120
不限时
解:(1)A,B,C
三种方式的月上网费用yA(元)、yB(元)、yC(元)关于每月上网时间t(小时)的函数表达式为
yA=
30,
0≤t≤25;
30+3(t-25)=3t-45,
t>25.
50,
0≤t≤50;
50+3(t-50)=3t-100,t>50.
yB=
yC=120.
你打算用“形”的方式还是“数”的方式解决?
yA=
30,
0≤t≤25;
3t-45,
t>25.
50,
0≤t≤50;
3t-100,t>50.
yB=
yC=120.
yC
120
50
30
25
50
75
O
t
y
yA
yB
根据省钱原则选择方案
(h)
(元)
A
B
C
(2)选取哪种方式能节省上网费?
(1)
小结与回顾
这节课,
(1)你学习到什么新知识?
(2)获得了什么经验?
(3)需要注意什么?
利用一次函数进行方案选择
(1)确定函数表达式;
(2)求交点;
注意:选择方案的依据
(3)“数”的策略:解方程、不等式
“形”的策略:画图像,看图说话.
修得一个用数学思维思考世界的头脑
练就一双用数学视角观察世界的眼睛
——————方案专题
1、已知y1=2x,
y2=x+3
若y1=y2,则x=________
若y1>y2,则x的取值范围是_______
若y1
x>3
x<3
2、已知y1,
y2关于x的函数如图所示
若y1=y2,则x=________
若y1
3
x>3
x<3
O
y
3
y1
6
y2
x
(1)若目的地距离学校1000km,租用哪家租赁公司的汽车合算?你用什么方法来判断?
P
Q
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
1000
y/元
1000
y1
y2
2000
2000
3000
3000
分析:
x=1000时,
x/km
y1
y1与y2
谁更小.
(2)用车里程多少时,甲、乙两公司的租车费相等?
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
1000
x/km
y/元
1000
y1
y2
2000
2000
3000
3000
分析:
x=________时,y1=y2.
2000
(3)若学校租车的预算是3000元,那么租用哪家租赁公司的汽车合算?为什么?
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
1000
y/元
2000
1000
y1
y2
2000
3000
3000
分析:
y=3000时,
x/km
x甲与x乙
谁更大.
x甲
(4)如果根据用车里程来选择汽车租赁公司,你能给些建议吗?说说你的理由.
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
y/元
2000
1000
y1
y2
2000
x/km
当里程x=2000千米时,
两家均可;
当里程x<2000千米时,
选甲公司;
当里程x>2000千米时,
选乙公司;
根据省钱原则选择方案
1.某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示,当租书时间为120天时,应使用
比较合算.
会员卡
试一试
2、如图中,l1反映了某公司产品的销售额与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图象判断该公司盈利时销售量为(
)
(A)小于4件
(B)大于4件
(C)等于4件
(D)大于或等于4件
X(件)
Y(元)
1
2
3
4
5
6
100
200
300
400
500
l1
l2
O
B
交点的意义是什么?
(4)如果根据用车里程来选择汽车租赁公司,你能给些建议吗?说说你的理由.
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
O
y/元
2000
1000
y1
y2
2000
x/km
O
x/km
y/元
1000
y1
y2
2000
2500
3000
3000
2000
如果根据用车里程来选择汽车租赁公司,你能给些建议吗?说说你的理由.
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲、乙两家公司的出租汽车收取的租费分别是y1(元)和y2(元),它们都是用车里程x
(千米)的函数,图像如图所示.
=x
=0.5x+1000
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲汽车出租公司按每100
千米100元收取租车费;乙汽车出租公司按每100千米50元收取租车费,另加管理费800元.如果根据用车路程来选择,试判断租用哪家公司的汽车费用较少?
分析:先确定函数表达式;再求交点
学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同。甲汽车出租公司按每100
千米100元收取租车费;乙汽车出租公司按每100千米50元收取租车费,另加管理费1000元.如果根据用车路程来选择,试判断租用哪家公司的汽车费用较少?
解:设用车里程x
(千米)时,甲、乙两家公司收取的租费分别是y1(元)和y2(元)。
则
y1=x
y2=0.5x+1000
O
x/km
y/元
1000
y1=x
y2=0.5x+1000
2000
2000
从“形”上看
x=2000.一样
从“数”上看
(1)
由y1=y2.
得x=
0.5x+1000
,
x<2000.
选甲
(2)
由y1<y2.
得x<0.5x+1000
,
x>2000.选乙
(3)
由y1>y2.
得x>
0.5x+1000
,
甲汽车出租公司按每100千米100元收取租车费;乙汽车出租公司按每100千米50元收取租车费,另加管理费800元.如果根据用车路程来选择,试判断租用哪家公司的汽车费用较少?
1000
x/km
y/元
1000
y1
y2
2000
2000
3000
3000
O
x/km
y/元
1000
y1
2500
3000
3000
y2
(1)确定函数表达式;
(3)“数”的策略:解方程、不等式
(2)求交点;
利用一次函数进行租车等方案选择的一般步骤:
注意:
“形”的策略:画图像,看图说话.
选择方案的依据
A、B两家旅行社分别推出家庭旅游优惠活动,两家旅行社的票价均为90元/人,但优惠办法不同.A旅行社的优惠办法是:全家有一人购全票,其余的人半价优惠;B旅行社的优惠办法是:每人均按三分之二的票价优惠.
y1=90+45(x-1),
解:(1)
y2=60x
(1)请分别写出A、B两旅行社收费y1元、y2元与家庭人数为x人之间的函数表达式.
(2)你将选择哪家旅行社?
即y1=45x+45
y1=45x+45,
解:(1)
y2=60x,
x=3.
由y1=y2.
得45x+45=
60x
,
x>3
由y1<y2.
x<3.
由y1>y2.
法一:(数)
得45x+45<
60x
,
得45x+45>
60x
,
综上,当家庭人数为3人时,两家收费相同,均为180元;
当家庭人数大于3人时,选A旅行社
当家庭人数小于3人时,选B旅行社
(2)
O
y/元
3
y1
y2
180
法二:(形)
45
得交点(3,180).
由.
y=45x+45,
由图可知.
y=60x,
x/人
某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参考数据如下:
(1)请分别写出汽车、火车运输总费用y1(元)、y2(元)与运输路程x(千米)之间的函数表达式.
(2)你认为用哪种运输方式好?
运输方式
速度/(千米/时)
途中综合费用/
(元/时)
装卸费用/(元)
汽车
60
270
200
火车
100
240
410
解:(1)
即y1=4.5x+200
即y2=2.4x+410
O
20
x/千米
y/元
100
200
y1
y2
400
650
运输方式
速度/(千米/时)
途中综合费用/
(元/时)
装卸费用/(元)
汽车
60
270
200
火车
100
240
410
解:(1)
即y1=4.5x+200
即y2=2.4x+410
(2)
得交点(100,650).
由.
y=4.5x+200,
y=2.4x+410,
由图可知.
当运输路程为100千米时,两种运输方式费用相同,均为650元;
当运输路程小于100千米时,选汽车
当运输路程大于100千米时,选火车
下表给出A,B,C
三种上宽带网的收费方式:
收费方式
月使用费/元
包时上网时间/h
超时费/(元/h)
A
30
25
3
B
50
50
3
C
120
不限时
试金石
(1)请分别写出A,B,C
三种方式的月上网费用yA(元)、yB(元)、yC(元)关于每月上网时间t(小时)的函数表达式.
(2)选取哪种方式能节省上网费?
收费方式
月使用费/元
包时上网时间/h
超时费/(元/h)
A
30
25
3
B
50
50
3
C
120
不限时
解:(1)A,B,C
三种方式的月上网费用yA(元)、yB(元)、yC(元)关于每月上网时间t(小时)的函数表达式为
yA=
30,
0≤t≤25;
30+3(t-25)=3t-45,
t>25.
50,
0≤t≤50;
50+3(t-50)=3t-100,t>50.
yB=
yC=120.
你打算用“形”的方式还是“数”的方式解决?
yA=
30,
0≤t≤25;
3t-45,
t>25.
50,
0≤t≤50;
3t-100,t>50.
yB=
yC=120.
yC
120
50
30
25
50
75
O
t
y
yA
yB
根据省钱原则选择方案
(h)
(元)
A
B
C
(2)选取哪种方式能节省上网费?
(1)
小结与回顾
这节课,
(1)你学习到什么新知识?
(2)获得了什么经验?
(3)需要注意什么?
利用一次函数进行方案选择
(1)确定函数表达式;
(2)求交点;
注意:选择方案的依据
(3)“数”的策略:解方程、不等式
“形”的策略:画图像,看图说话.
修得一个用数学思维思考世界的头脑
练就一双用数学视角观察世界的眼睛
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
