苏科版九年级数学上册 4.3 等可能条件下的概率(二)(共12张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 4.3 等可能条件下的概率(二)(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 634.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
4.3 等可能条件下的概率(二)
九年级(上册)
初中数学
已知一个带指针的转盘,指针的位置固定,转动转盘后任其自由停止,如果在某个时刻观察指针的位置.
(1)这时所有可能的结果有多少个?为什么?
(2)每个结果出现的机会是均等的吗?
4.3
等可能条件下的概率(二)
现将转盘分成8个面积相等的扇形,若每个扇形面积为单位1,转动转盘,转盘指针指向的位置在不断改变(指针指向两个扇形的交线时,当作指向右边的扇形).
(2)怎样求指针指向每一个扇形区域的概率呢?
(1)当转盘停止时,指针指向每一个扇形区域的机会均等吗?
4.3
等可能条件下的概率(二)
4.3
等可能条件下的概率(二)
1、一只小狗在如图所示的方砖上自由走来走去,最终停留在黑色方砖上的概率是_____。
2、小红制作一个转盘,并将其分成12个扇形,将其中的3块扇形涂上黑色,4块涂上红色,其余涂上白色,转动转盘上的指针,指针停止后,指向黑色的概率为
_____,指向红色的概率为_______
,指向白色的概率为
________。
4.3
等可能条件下的概率(二)
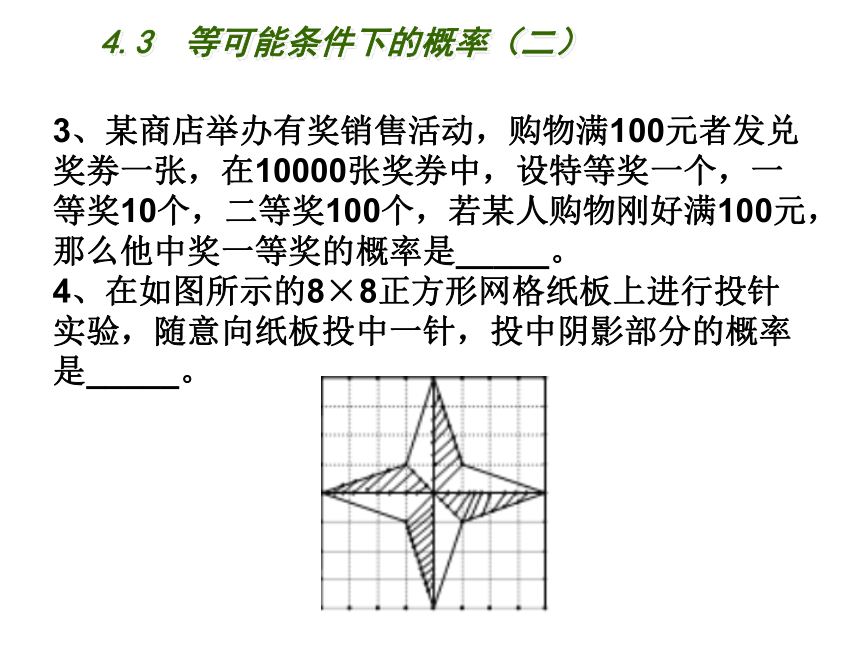
3、某商店举办有奖销售活动,购物满100元者发兑奖劵一张,在10000张奖券中,设特等奖一个,一等奖10个,二等奖100个,若某人购物刚好满100元,那么他中奖一等奖的概率是_____。
4、在如图所示的8×8正方形网格纸板上进行投针实验,随意向纸板投中一针,投中阴影部分的概率是_____。
现将转盘涂色,颜色为红、蓝、白三种颜色.
(1)转动转盘的试验所有等可能出现的结果数?
(2)事件指针指向红色区域可能发生的结果数?
(3)怎样计算指针指向红色区域的概率?
(4)你能计算出指针指向白色区域的概率吗?
4.3
等可能条件下的概率(二)
“指针指向红色区域”与“指针不指向红色区域”这两个事件及概率之间有怎样的联系,你有何发现?
4.3
等可能条件下的概率(二)
例 某商场制作了一个可以自由转动的转盘(如图),转盘分为24个相同的扇形,其中红色扇形1个、蓝色扇形3个、黄色扇形5个、白色扇形15个.商场规定:顾客每购满1000元的商品,可获得一次转动转盘的机会.当转盘停止转动时,指针指向红、蓝、黄区域,顾客可分别获得500元、100元、50元的礼品.某顾客购物1400元,他获得礼品的概率是多少?获得500元、100元、50元礼品的概率各是多少?
4.3
等可能条件下的概率(二)
4.3
等可能条件下的概率(二)
设计一个转盘,任意转动转盘1次,当转盘停止转动时使得指针:
(1)指向红色区域的概率为
,
指向黄色区域的概率为
,
指向蓝色区域的概率为
;
(2)指向红色区域的概率为
,
指向黄色区域的概率为
,
指向蓝色区域的概率为
.
4.3
等可能条件下的概率(二)
例2、在4m远处向地毯扔沙包(如图12-5地毯中每一块小正方形除颜色外完全相同),假设沙包击中每一块小正方形是等可能的。扔沙包1次,击中红色区域的概率多大?
问题1:这个问题可转化为等可能条件下的概率(一)吗?
4.3
等可能条件下的概率(二)
问题2:在试验过程中,这些正方形除颜色外都相同,每扔一次沙包一次击中每一块小正方形的可能性都相同吗?
问题3:在试验过程中每扔一次沙包所有可能发生的结果有多少个?击中红色区域的可能性结果有几个?概率是多少?
问题4:若扔沙包2次,分别击中红、白的概率是多少?
4.3
等可能条件下的概率(二)
4.3 等可能条件下的概率(二)
九年级(上册)
初中数学
已知一个带指针的转盘,指针的位置固定,转动转盘后任其自由停止,如果在某个时刻观察指针的位置.
(1)这时所有可能的结果有多少个?为什么?
(2)每个结果出现的机会是均等的吗?
4.3
等可能条件下的概率(二)
现将转盘分成8个面积相等的扇形,若每个扇形面积为单位1,转动转盘,转盘指针指向的位置在不断改变(指针指向两个扇形的交线时,当作指向右边的扇形).
(2)怎样求指针指向每一个扇形区域的概率呢?
(1)当转盘停止时,指针指向每一个扇形区域的机会均等吗?
4.3
等可能条件下的概率(二)
4.3
等可能条件下的概率(二)
1、一只小狗在如图所示的方砖上自由走来走去,最终停留在黑色方砖上的概率是_____。
2、小红制作一个转盘,并将其分成12个扇形,将其中的3块扇形涂上黑色,4块涂上红色,其余涂上白色,转动转盘上的指针,指针停止后,指向黑色的概率为
_____,指向红色的概率为_______
,指向白色的概率为
________。
4.3
等可能条件下的概率(二)
3、某商店举办有奖销售活动,购物满100元者发兑奖劵一张,在10000张奖券中,设特等奖一个,一等奖10个,二等奖100个,若某人购物刚好满100元,那么他中奖一等奖的概率是_____。
4、在如图所示的8×8正方形网格纸板上进行投针实验,随意向纸板投中一针,投中阴影部分的概率是_____。
现将转盘涂色,颜色为红、蓝、白三种颜色.
(1)转动转盘的试验所有等可能出现的结果数?
(2)事件指针指向红色区域可能发生的结果数?
(3)怎样计算指针指向红色区域的概率?
(4)你能计算出指针指向白色区域的概率吗?
4.3
等可能条件下的概率(二)
“指针指向红色区域”与“指针不指向红色区域”这两个事件及概率之间有怎样的联系,你有何发现?
4.3
等可能条件下的概率(二)
例 某商场制作了一个可以自由转动的转盘(如图),转盘分为24个相同的扇形,其中红色扇形1个、蓝色扇形3个、黄色扇形5个、白色扇形15个.商场规定:顾客每购满1000元的商品,可获得一次转动转盘的机会.当转盘停止转动时,指针指向红、蓝、黄区域,顾客可分别获得500元、100元、50元的礼品.某顾客购物1400元,他获得礼品的概率是多少?获得500元、100元、50元礼品的概率各是多少?
4.3
等可能条件下的概率(二)
4.3
等可能条件下的概率(二)
设计一个转盘,任意转动转盘1次,当转盘停止转动时使得指针:
(1)指向红色区域的概率为
,
指向黄色区域的概率为
,
指向蓝色区域的概率为
;
(2)指向红色区域的概率为
,
指向黄色区域的概率为
,
指向蓝色区域的概率为
.
4.3
等可能条件下的概率(二)
例2、在4m远处向地毯扔沙包(如图12-5地毯中每一块小正方形除颜色外完全相同),假设沙包击中每一块小正方形是等可能的。扔沙包1次,击中红色区域的概率多大?
问题1:这个问题可转化为等可能条件下的概率(一)吗?
4.3
等可能条件下的概率(二)
问题2:在试验过程中,这些正方形除颜色外都相同,每扔一次沙包一次击中每一块小正方形的可能性都相同吗?
问题3:在试验过程中每扔一次沙包所有可能发生的结果有多少个?击中红色区域的可能性结果有几个?概率是多少?
问题4:若扔沙包2次,分别击中红、白的概率是多少?
4.3
等可能条件下的概率(二)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
