2021-2022学年黑龙江省哈尔滨市香坊区德强中学八年级(上)周测数学试卷(9.20)(Word版 无答案)
文档属性
| 名称 | 2021-2022学年黑龙江省哈尔滨市香坊区德强中学八年级(上)周测数学试卷(9.20)(Word版 无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 191.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览


文档简介
2021-2022学年黑龙江省哈尔滨市香坊区德强中学八年级(上)周测数学试卷(9.20)(五四学制)
一、选择题(每题3分,共30分)
1.点M(﹣1,2)关于x轴对称的点的坐标为( )
A.(﹣1,﹣2)
B.(﹣1,2)
C.(1,﹣2)
D.(2,﹣1)
2.如图,其中是轴对称图形的是( )
A.
B.
C.
D.
3.下列计算正确的是( )
A.b3 b3=2b3
B.(ab2)3=ab6
C.(a5)2=a10
D.(a3)2 a4=a9
4.到△ABC的三个顶点距离相等的点是( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高线的交点
D.三条边的垂直平分线的交点
5.如图,在△ABC中,AB=AC,BD=DC,则下列结论中错误的是( )
A.∠1=∠2
B.∠BAC=∠B
C.AD⊥BC
D.∠B=∠C
6.等腰三角形的一个角是90°,则它的底角是( )
A.30°
B.45°
C.60°
D.90°
7.如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则图中的等腰三角形共有( )
A.1个
B.2个
C.3个
D.4个
8.如图,在△ABC中,DE垂直平分AC,若BC=8,AB=10,则△EBC的周长为( )
A.16
B.28
C.26
D.18
9.下列三角形:①有两个角等于60°;有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形.其中是等边三角形的有( )
A.①②
B.②
C.①③
D.①②③
10.如图,正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A.6
B.7
C.8
D.9
二、填空题(每题3分,共30分)
11.45×(0.25)5=
.
12.若27=24 2x,则x=
.
13.等腰三角形两边长为1和2,则它的周长为
.
14.等边三角形中两条中线所夹的钝角的度数为
.
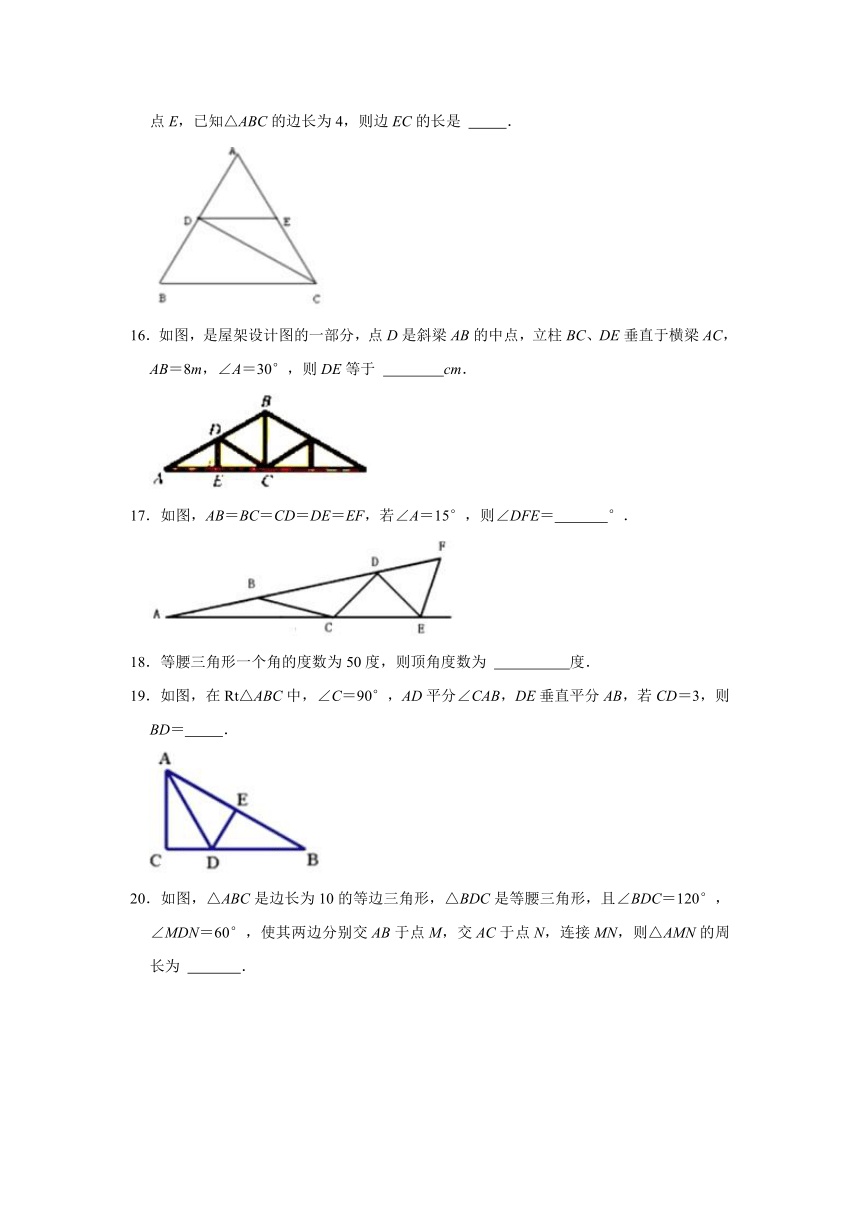
15.如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则边EC的长是
.
16.如图,是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE等于
cm.
17.如图,AB=BC=CD=DE=EF,若∠A=15°,则∠DFE=
°.
18.等腰三角形一个角的度数为50度,则顶角度数为
度.
19.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE垂直平分AB,若CD=3,则BD=
.
20.如图,△ABC是边长为10的等边三角形,△BDC是等腰三角形,且∠BDC=120°,∠MDN=60°,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为
.
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.计算:(1)x2 x4﹣3(x3)2;
(2)(﹣3a3b)2+2a2 a4 (﹣b)2﹣4a6b2.
22.如图,△ABC的三个顶点的坐标分别为A(﹣6,4),B(﹣4,0),C(﹣2,2).
(1)将△ABC向下平移5个单位,得到△A1B1C1.画出图形,并直接写出点A1的坐标;
(2)作△ABC关于y轴的轴对称图形,得到△A2B2C2.画出图形,并直接写出点B2的坐标.
23.如图,某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M在北偏东30°方向处,问B处与灯塔M的距离是多少海里?
24.如图,在△ABC中,AC=BC,∠C=90°,AD平分∠BAC,BE⊥AE.
(1)求证:BEAD;
(2)连结CE,求∠CED的度数.
25.一个电器超市购进A、B两种型号的电风扇进行销售,若一台A种型号的进价比一台B种型号的进价多30元,购进A种型号3台比购进B种型号2台多用260元.
(1)求每台A种型号和B种型号的电风扇进价分别是多少元;
(2)该超市A种型号电风扇每台售价260元,B种型号电风扇每台售价190元,超市根据市场需求,决定再采购,这两种型号的电风扇共30台,若本次购进的两种电风扇全部售出后,总获利不少于1400元,求该超市本次购进A种型号的电风扇至少是多少台?
26.如图,A(0,6),B(﹣4,0),点关于y轴的对称点为C点,△ABD的面积是30.
(1)求点D坐标.
(2)若动点P从点B出发,沿射线BC运动,速度为每秒1个单位,设P的运动时间为t秒,△APC的面积为S,求S与t的关系式.(不要求写出t的取值范围)
(3)在(2)的条件下,同时点Q从D点出发沿y轴正方向以每秒2个单位速度匀速运动,若点R在过A点且平行于x轴的直线上,当△PQR为等腰直角三角形时,请直接写出满足条件的t值.
27.如图,△ABC的∠ABC的平分线BD与∠ACB的外角平分线交于D点.
(1)DE∥BC交BA的延长线于E,交CA延长线于F,求证:CF=EF+BE.
(2)在(1)的条件下,如图(2),若∠ACB=30°,∠ABC=90°,DE=2,求△FCD的面积.
一、选择题(每题3分,共30分)
1.点M(﹣1,2)关于x轴对称的点的坐标为( )
A.(﹣1,﹣2)
B.(﹣1,2)
C.(1,﹣2)
D.(2,﹣1)
2.如图,其中是轴对称图形的是( )
A.
B.
C.
D.
3.下列计算正确的是( )
A.b3 b3=2b3
B.(ab2)3=ab6
C.(a5)2=a10
D.(a3)2 a4=a9
4.到△ABC的三个顶点距离相等的点是( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高线的交点
D.三条边的垂直平分线的交点
5.如图,在△ABC中,AB=AC,BD=DC,则下列结论中错误的是( )
A.∠1=∠2
B.∠BAC=∠B
C.AD⊥BC
D.∠B=∠C
6.等腰三角形的一个角是90°,则它的底角是( )
A.30°
B.45°
C.60°
D.90°
7.如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则图中的等腰三角形共有( )
A.1个
B.2个
C.3个
D.4个
8.如图,在△ABC中,DE垂直平分AC,若BC=8,AB=10,则△EBC的周长为( )
A.16
B.28
C.26
D.18
9.下列三角形:①有两个角等于60°;有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形.其中是等边三角形的有( )
A.①②
B.②
C.①③
D.①②③
10.如图,正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A.6
B.7
C.8
D.9
二、填空题(每题3分,共30分)
11.45×(0.25)5=
.
12.若27=24 2x,则x=
.
13.等腰三角形两边长为1和2,则它的周长为
.
14.等边三角形中两条中线所夹的钝角的度数为
.
15.如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则边EC的长是
.
16.如图,是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE等于
cm.
17.如图,AB=BC=CD=DE=EF,若∠A=15°,则∠DFE=
°.
18.等腰三角形一个角的度数为50度,则顶角度数为
度.
19.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE垂直平分AB,若CD=3,则BD=
.
20.如图,△ABC是边长为10的等边三角形,△BDC是等腰三角形,且∠BDC=120°,∠MDN=60°,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为
.
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.计算:(1)x2 x4﹣3(x3)2;
(2)(﹣3a3b)2+2a2 a4 (﹣b)2﹣4a6b2.
22.如图,△ABC的三个顶点的坐标分别为A(﹣6,4),B(﹣4,0),C(﹣2,2).
(1)将△ABC向下平移5个单位,得到△A1B1C1.画出图形,并直接写出点A1的坐标;
(2)作△ABC关于y轴的轴对称图形,得到△A2B2C2.画出图形,并直接写出点B2的坐标.
23.如图,某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M在北偏东30°方向处,问B处与灯塔M的距离是多少海里?
24.如图,在△ABC中,AC=BC,∠C=90°,AD平分∠BAC,BE⊥AE.
(1)求证:BEAD;
(2)连结CE,求∠CED的度数.
25.一个电器超市购进A、B两种型号的电风扇进行销售,若一台A种型号的进价比一台B种型号的进价多30元,购进A种型号3台比购进B种型号2台多用260元.
(1)求每台A种型号和B种型号的电风扇进价分别是多少元;
(2)该超市A种型号电风扇每台售价260元,B种型号电风扇每台售价190元,超市根据市场需求,决定再采购,这两种型号的电风扇共30台,若本次购进的两种电风扇全部售出后,总获利不少于1400元,求该超市本次购进A种型号的电风扇至少是多少台?
26.如图,A(0,6),B(﹣4,0),点关于y轴的对称点为C点,△ABD的面积是30.
(1)求点D坐标.
(2)若动点P从点B出发,沿射线BC运动,速度为每秒1个单位,设P的运动时间为t秒,△APC的面积为S,求S与t的关系式.(不要求写出t的取值范围)
(3)在(2)的条件下,同时点Q从D点出发沿y轴正方向以每秒2个单位速度匀速运动,若点R在过A点且平行于x轴的直线上,当△PQR为等腰直角三角形时,请直接写出满足条件的t值.
27.如图,△ABC的∠ABC的平分线BD与∠ACB的外角平分线交于D点.
(1)DE∥BC交BA的延长线于E,交CA延长线于F,求证:CF=EF+BE.
(2)在(1)的条件下,如图(2),若∠ACB=30°,∠ABC=90°,DE=2,求△FCD的面积.
同课章节目录
