3.1建立一元一次方程模型 湘教版初中数学七年级上册 课件(27张)
文档属性
| 名称 | 3.1建立一元一次方程模型 湘教版初中数学七年级上册 课件(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1014.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
3.1 建立一元一次方程模型
第3章 一元一次方程
导入新课
讲授新课
当堂练习
课堂小结
教学课件
学习目标
1.理解方程、一元一次方程及方程的解的概念.
2.会根据具体问题中的等量关系列出一元一次方程.(重点、难点)
叔叔的年龄乘以2再减去18刚好为70,那现在你能知道叔叔的年龄吗?你是怎么猜?
小游戏:猜叔叔的年龄
导入新课
情境引入
讲授新课
一元一次方程的概念与一元一次方程的解
一
合作探究
小敏,我能猜出你年龄.
小敏
不信
你的年龄乘2减8得数是多少?
你今年17岁
26
她怎么知道我的年龄是17岁的呢?
如果设小敏的年龄为x岁,那么“乘2再减8”就是 ,因此可以得到等量关系: .
2x-8
2x-8=26
情景1:
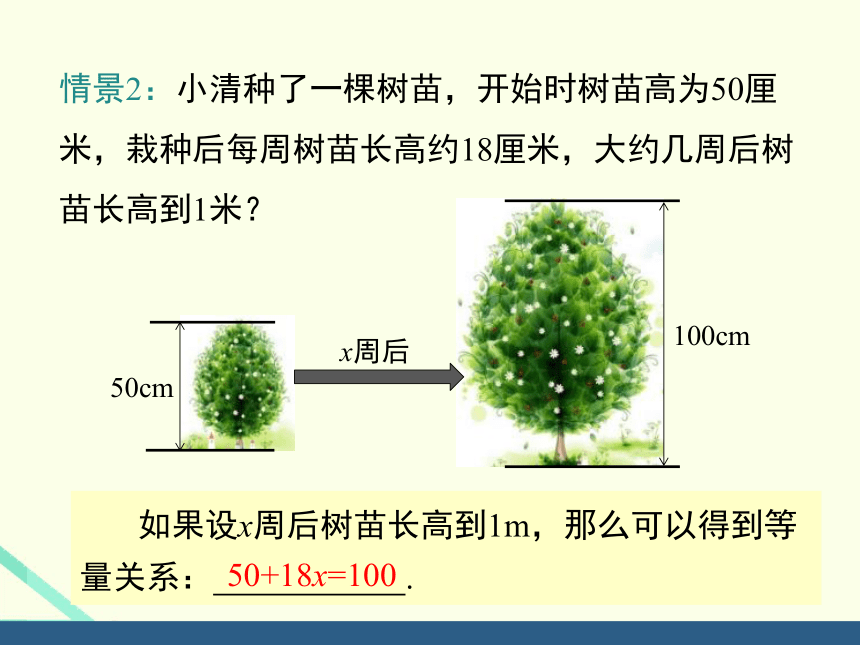
情景2:小清种了一棵树苗,开始时树苗高为50厘米,栽种后每周树苗长高约18厘米,大约几周后树苗长高到1米?
50cm
100cm
x周后
如果设x周后树苗长高到1m,那么可以得到等量关系: .
50+18x=100
像 2x-8=26这样, 含有未知数的等式叫做方程.
方程的有关概念
你能列举出其他的是方程的例子吗?
像上面这样,把所要求的量用字母x(或y,…)表示,根据问题中的等量关系列出方程,这一过程叫做建立方程.
概念学习
“方程”一词最早来源于中国的《九章算术》.我国古代数学家刘徽注释“方程”的含义时,指出 “程”字指列出含未知数的等式.
知识链接
“方程的来历”
法国数学家笛卡尔最早提出方程的数学概念.
他提出用字母表示未知数,用运算符号和等号将字母与数字连接起来,就形成了含有未知数的等式.
知识链接
“方程的来历”
议一议
(1)方程2x-8=26,50+18x=100,有什么共同特点?
(2)满足什么条件的方程是一元一次方程?
一元一次方程的定义
在一个方程中,只________________,并且______________是1,且等式两边都是整式,这样的方程叫做一元一次方程.
含有一个未知数
未知数的次数
概念学习
做一做
判断下列各式是不是一元一次方程.
①2x2-6=5;②-m+7=2;③x=2;④x+y=2;
⑤x+4>0;⑥2x2-2(x2-x)=1;⑦ ;⑧πx=14.
①只含有一个未知数;
②未知数的指数是1;
③方程中的代数式都是整式.
判断一个方程是一元一次方程,化简后必须满足三个条件:
√
√
√
√
典例精析
例1 若关于x的方程3xm-2+5=0是一元一次方程,求m的值.
解:根据一元一次方程的定义可知
m-2 =1,
所以 m =3.
1. 是一元一次方程,则k=______
3. 是一元一次方程,k=_____
2. 是一元一次方程,则k =_____
1或-1
-1
-2
注意:未知数的次数为1,且系数不等于0
变式训练
在程 x+5=9中,有同学算得x=4,这个答案正确吗
把x=4代入方程两边,
左边= 4+5=9,右边=9,
左边=右边,
所以x=4 是方程x+5=9的解.
代入
计算
比较
判断
想一想
在“猜年龄”游戏中,当被告知计算的结果是26时,我们所列的方程为2x-8=26,从而求出年龄是17.由于17能使方程的两边相等,我们就把17叫做方程2x-8=26的解.
方程的解的定义
使方程左、右两边的值相等的未知数的值,叫做方程的解.
概念学习
例2 检验下列x的值是否是方程2.5x+318=818的解.
(1) x = 200 (2) x = 230.
解:(1)把 x = 200 代入原方程得,
左边= 2.5×200+318=818,
左边=右边,
所以x=200是方程2.5x+318=818的解.
(2) 把 x =230 代入原方程得,
左边= 2.5×230+318=893,
左边≠右边,
所以x=230不是方程2.5x+318=818的解.
判断方程解的三个步骤:
(1)代:把所给未知数的值分别代入方程等号的左右两边.
(2)算:计算等号的左右两边的值.
(3)判:若左边=右边,则是方程的解;若左边≠右边,则不是方程的解.
方法总结
练一练
1.下列方程中,解为x=-3的是( )
A.3x-2=2x B.4x-1=2x+4
C.3x+1=2x-2 D.5x-3=6x-3
C
2.若x=5是关于x的方程a x=15的解,则a的值为______.
3
根据实际问题列一元一次方程
二
例3 根据下列问题,设未知数并列出方程
(1)用一根长36 cm的铁丝围成一个长方形,长方形的长比宽长2CM,长方形的长是多少?
解:设长方形的长为x cm.
等量关系:长方形的(长+宽) *2 =周长.
列方程:( X+X-2 )*2=36.
(2)一台计算机已使用1000 h,预计每月再使用250 h,经过多少月这台计算机的使用时间达到规定的检修时间2350 h?
解:设x月后这台计算机的使用时间达到2350 h
等量关系:已用时间+再用时间=检修时间.
列方程: 1000+250 x = 2350 .
请同学们思考:
(1)怎样将一个实际问题转化为方程问题?
(2)列方程的依据是什么?
实际问题
设未知数列方程
一元一次方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
抓关键句子找等量关系
1.小强买书花费58元钱,付款时恰好用了1元和5元的纸币共10张.设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
A.x+5(10-x)=58 B.x+5(x-10)=58
C.x+10(x-5)=58 D.5x+(10-x)=58
A
练一练
2.某旅游团共有50人,其中男生比女生多8人,那么该旅游团男生和女生分别有多少人?根据题意设未知数并列出方程。
分析:题中等量关系为:男生人数+女生人数=总人数
解:设女生人数有x人,则男生人数为(x+8)人,
(x+8)+x=50
根据等量关系“男生人数+女生人数=总人数”,则有:
当堂练习
1.下列各式中,是一元一次方程的有______(填序号).
(1) +12=3;(2) 19-x;(3) 1=2x+3;
(4) 5x2=25;(5) x+y=9;(6) 3x+5=3x+1.
2.x=2________方程3x-2=3的解.(填“是”或“不是”)
(1)(3)
不是
3.若关于x的方程(k-2)x|k-1|+4=0是一元一次方程,则k=____.
0
4.小章准备用自己节省的零花钱购买一台MP4来学习英语,他已存有100元,并计划从本月起每月节省40元,直到他有360元.设x个月后小章有360元,则可列出计算月数的方程为( )
A.40x+100=360 B.40x-100=360
C.x-100=360 D.x+100=360
A
5.已知x=2是方程mx=x+2的解,求m2-3m+1的值.
解:因为x=2是方程mx=x+2的解,
所以m=(2+2)/2,故m=2,
当m=2时,m2-3m+1=4-3×2+1=-1.
课堂小结
建立一元一次方程模型
方程的有关概念
一元一次方程的概念
建立一元一次方程模型
设字母表示数
把其他部分的量也用字母表示出来
找等量关系,列出方程
方程的概念
方程的解概念
3.1 建立一元一次方程模型
第3章 一元一次方程
导入新课
讲授新课
当堂练习
课堂小结
教学课件
学习目标
1.理解方程、一元一次方程及方程的解的概念.
2.会根据具体问题中的等量关系列出一元一次方程.(重点、难点)
叔叔的年龄乘以2再减去18刚好为70,那现在你能知道叔叔的年龄吗?你是怎么猜?
小游戏:猜叔叔的年龄
导入新课
情境引入
讲授新课
一元一次方程的概念与一元一次方程的解
一
合作探究
小敏,我能猜出你年龄.
小敏
不信
你的年龄乘2减8得数是多少?
你今年17岁
26
她怎么知道我的年龄是17岁的呢?
如果设小敏的年龄为x岁,那么“乘2再减8”就是 ,因此可以得到等量关系: .
2x-8
2x-8=26
情景1:
情景2:小清种了一棵树苗,开始时树苗高为50厘米,栽种后每周树苗长高约18厘米,大约几周后树苗长高到1米?
50cm
100cm
x周后
如果设x周后树苗长高到1m,那么可以得到等量关系: .
50+18x=100
像 2x-8=26这样, 含有未知数的等式叫做方程.
方程的有关概念
你能列举出其他的是方程的例子吗?
像上面这样,把所要求的量用字母x(或y,…)表示,根据问题中的等量关系列出方程,这一过程叫做建立方程.
概念学习
“方程”一词最早来源于中国的《九章算术》.我国古代数学家刘徽注释“方程”的含义时,指出 “程”字指列出含未知数的等式.
知识链接
“方程的来历”
法国数学家笛卡尔最早提出方程的数学概念.
他提出用字母表示未知数,用运算符号和等号将字母与数字连接起来,就形成了含有未知数的等式.
知识链接
“方程的来历”
议一议
(1)方程2x-8=26,50+18x=100,有什么共同特点?
(2)满足什么条件的方程是一元一次方程?
一元一次方程的定义
在一个方程中,只________________,并且______________是1,且等式两边都是整式,这样的方程叫做一元一次方程.
含有一个未知数
未知数的次数
概念学习
做一做
判断下列各式是不是一元一次方程.
①2x2-6=5;②-m+7=2;③x=2;④x+y=2;
⑤x+4>0;⑥2x2-2(x2-x)=1;⑦ ;⑧πx=14.
①只含有一个未知数;
②未知数的指数是1;
③方程中的代数式都是整式.
判断一个方程是一元一次方程,化简后必须满足三个条件:
√
√
√
√
典例精析
例1 若关于x的方程3xm-2+5=0是一元一次方程,求m的值.
解:根据一元一次方程的定义可知
m-2 =1,
所以 m =3.
1. 是一元一次方程,则k=______
3. 是一元一次方程,k=_____
2. 是一元一次方程,则k =_____
1或-1
-1
-2
注意:未知数的次数为1,且系数不等于0
变式训练
在程 x+5=9中,有同学算得x=4,这个答案正确吗
把x=4代入方程两边,
左边= 4+5=9,右边=9,
左边=右边,
所以x=4 是方程x+5=9的解.
代入
计算
比较
判断
想一想
在“猜年龄”游戏中,当被告知计算的结果是26时,我们所列的方程为2x-8=26,从而求出年龄是17.由于17能使方程的两边相等,我们就把17叫做方程2x-8=26的解.
方程的解的定义
使方程左、右两边的值相等的未知数的值,叫做方程的解.
概念学习
例2 检验下列x的值是否是方程2.5x+318=818的解.
(1) x = 200 (2) x = 230.
解:(1)把 x = 200 代入原方程得,
左边= 2.5×200+318=818,
左边=右边,
所以x=200是方程2.5x+318=818的解.
(2) 把 x =230 代入原方程得,
左边= 2.5×230+318=893,
左边≠右边,
所以x=230不是方程2.5x+318=818的解.
判断方程解的三个步骤:
(1)代:把所给未知数的值分别代入方程等号的左右两边.
(2)算:计算等号的左右两边的值.
(3)判:若左边=右边,则是方程的解;若左边≠右边,则不是方程的解.
方法总结
练一练
1.下列方程中,解为x=-3的是( )
A.3x-2=2x B.4x-1=2x+4
C.3x+1=2x-2 D.5x-3=6x-3
C
2.若x=5是关于x的方程a x=15的解,则a的值为______.
3
根据实际问题列一元一次方程
二
例3 根据下列问题,设未知数并列出方程
(1)用一根长36 cm的铁丝围成一个长方形,长方形的长比宽长2CM,长方形的长是多少?
解:设长方形的长为x cm.
等量关系:长方形的(长+宽) *2 =周长.
列方程:( X+X-2 )*2=36.
(2)一台计算机已使用1000 h,预计每月再使用250 h,经过多少月这台计算机的使用时间达到规定的检修时间2350 h?
解:设x月后这台计算机的使用时间达到2350 h
等量关系:已用时间+再用时间=检修时间.
列方程: 1000+250 x = 2350 .
请同学们思考:
(1)怎样将一个实际问题转化为方程问题?
(2)列方程的依据是什么?
实际问题
设未知数列方程
一元一次方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
抓关键句子找等量关系
1.小强买书花费58元钱,付款时恰好用了1元和5元的纸币共10张.设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
A.x+5(10-x)=58 B.x+5(x-10)=58
C.x+10(x-5)=58 D.5x+(10-x)=58
A
练一练
2.某旅游团共有50人,其中男生比女生多8人,那么该旅游团男生和女生分别有多少人?根据题意设未知数并列出方程。
分析:题中等量关系为:男生人数+女生人数=总人数
解:设女生人数有x人,则男生人数为(x+8)人,
(x+8)+x=50
根据等量关系“男生人数+女生人数=总人数”,则有:
当堂练习
1.下列各式中,是一元一次方程的有______(填序号).
(1) +12=3;(2) 19-x;(3) 1=2x+3;
(4) 5x2=25;(5) x+y=9;(6) 3x+5=3x+1.
2.x=2________方程3x-2=3的解.(填“是”或“不是”)
(1)(3)
不是
3.若关于x的方程(k-2)x|k-1|+4=0是一元一次方程,则k=____.
0
4.小章准备用自己节省的零花钱购买一台MP4来学习英语,他已存有100元,并计划从本月起每月节省40元,直到他有360元.设x个月后小章有360元,则可列出计算月数的方程为( )
A.40x+100=360 B.40x-100=360
C.x-100=360 D.x+100=360
A
5.已知x=2是方程mx=x+2的解,求m2-3m+1的值.
解:因为x=2是方程mx=x+2的解,
所以m=(2+2)/2,故m=2,
当m=2时,m2-3m+1=4-3×2+1=-1.
课堂小结
建立一元一次方程模型
方程的有关概念
一元一次方程的概念
建立一元一次方程模型
设字母表示数
把其他部分的量也用字母表示出来
找等量关系,列出方程
方程的概念
方程的解概念
同课章节目录
