苏科版八年级数学上册 第4章 实数 复习(课件)(共20张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 第4章 实数 复习(课件)(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 510.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 14:10:23 | ||
图片预览





文档简介
(共20张PPT)
第4章 实数 复习课件
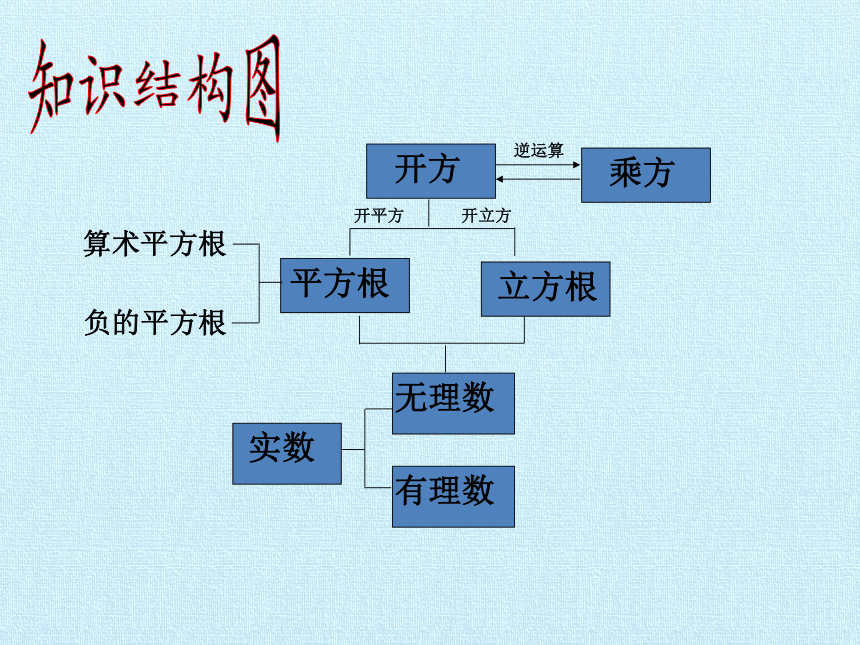
立方根
有理数
无理数
实数
算术平方根
负的平方根
平方根
开方
乘方
逆运算
开平方
开立方
知识结构图
1.16的平方根是( )
A.4 B.±4 C.256 D.±256
2.9的算术平方根是( )
A.3 B.±3 C.-3 D.81
3.8的立方根是( )
A.4 B.±4 C.2 D.±2
4.正数有 个平方根,0有 个平方根,负数
平方根。
5.正数有 个立方根,0有 个立方根,负数有 个立方根。
6.平方根等于本身的数有 ,算术平方根等于它本身的数是 ,立方根等于本身的数有 。
平方根、立方根、实数知多少?
B
A
C
两
一
没有
一
一
一
0
1和0
1、-1和0
7.填空: = ;
= ;
= ;
= ;
= ;
= ;
= ;
= ;
3
0.5
2
3
4
-5
±1
±1/2
8.判断下列说法是否正确:
(1)实数不是有理数就是无理数( )
(2)无限小数都是无理数( )
(3)无理数都是无限小数( )
(4)带根号的数都是无理数( )
(5)两个无理数之和一定是无理数( )
(6)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数( )
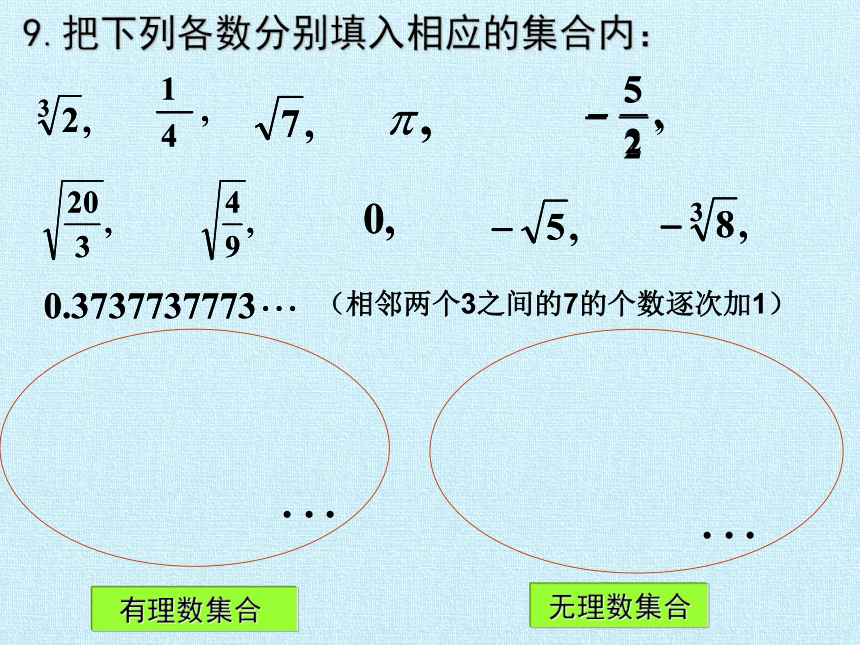
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
9.把下列各数分别填入相应的集合内:
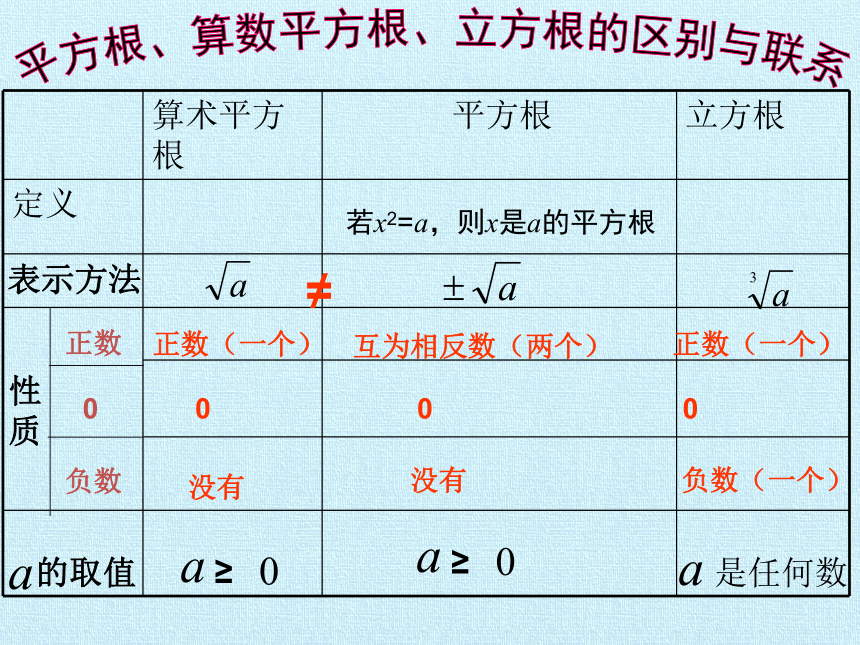
算术平方根 平方根 立方根
定义
表示方法
的取值
性质
≥
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
≠
平方根、算数平方根、立方根的区别与联系
若x2=a,则x是a的平方根
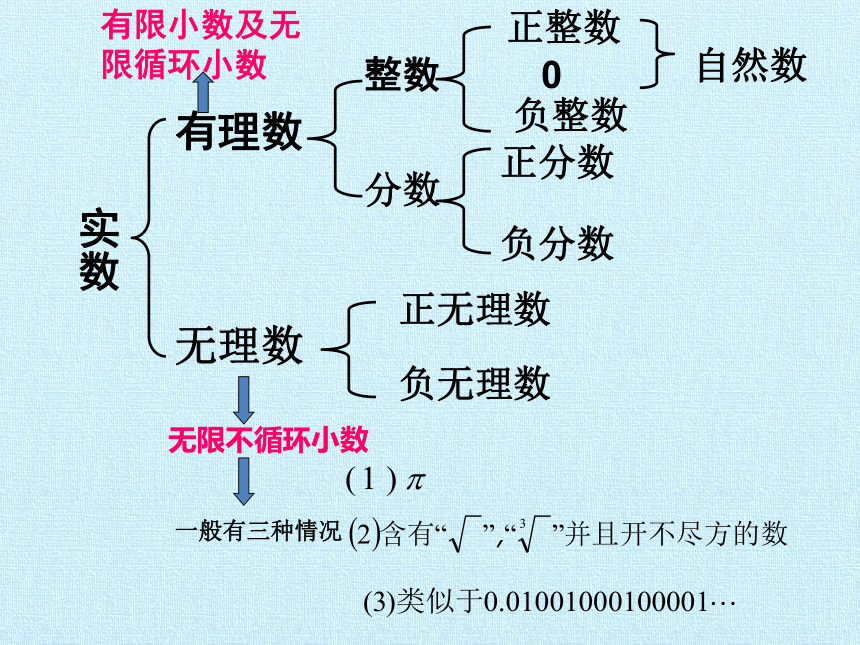
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.与数轴上的点一一对应的数是( )
A.有理数 B.无理数 C.实数 D.整数
4. 最小值是 ,此时a的取值是 。
2.估算 的值在整数( )之间
A.1到4 B.1到2 C.3到4 D.2到4
3.如果一个数的平方根是-3,那么它的另一个平方根是 。
C
B
3
2
-1
题组训练
例1:如果一个正数的平方根为a+1和 2a-7,求这个数。
解:由题意得:(a+1)+(2a-7)=0
解得a=2
所以a+1=3,2a-7=-3
所以这个数是9
典例分析
举一反三
1、已知2a-1的平方根是±3,b+1的算术平方根是2,则a= ,b= 。
2、已知x-1的平方根是±4,x+y-1的立方根是2,则x= ,y= 。
5
3
17
-8
例2:已知 与 互为相反数,求(x-2y)2的平方根。
解:因为 与 互为相反数
所以 + =0
所以 x-y+3=0 x=-1
x+y-1=0 解得 y=2
所以(x-2y)2=25, (x-y)2的平方根是±5
典例分析
1、已知 ,求
的值 ;
2、已知 ,求2x+y的立方根。
解(1)由题意得
b-2c-1 =0 b=5
c-2=0 解得 c=2
所以b+2c=9
所以 =3
解(2)由题意得
2x-y=0 x=2
x-2=0 解得 y=4
所以2x+y=8
所以2x+y的立方根是2
拓展提高
例3:求下面各式中的x的值
(1)(x-1)2=4 (2)3(x-3)3-24=0
解:(1)x-1=±2
x-1=2或x-1=-2
x=3或-1
解:(2)3(x-3)3=24
(x-3)3=8
x-3=2
x=5
整体思想、转化思想、分类思想
典例分析
学以致用
1.小明家客厅里5块正方形地砖的面积为32000cm2,求每一块正方形地砖的边长。
2.一块直角三角形的花坛,它的两条直角边c长分别为5m,12m,求它的斜边长。
5
12
课堂聚焦
今日事,今日毕
交流学习心得,体会丰收喜悦
平方根、立方根、实数
数学思想:
分类思想、方程思想、数形结合思想及转化思想。
小结
登高才能望远,才能看到最美的风景;探索才有收获,才能感受到真正的快乐!
愿同学们能够把握知识命脉成为一个快乐的探索者。
!
祝:同学们学习进步,
天天 开心!
1.已知a、b满足b = 则a= ,b= 。
2.已知 的小数部分是a,
的小数部分是b,a= , b= ,a+b的平方根是 。
挑战自我
5
-4
±1
谢 谢
第4章 实数 复习课件
立方根
有理数
无理数
实数
算术平方根
负的平方根
平方根
开方
乘方
逆运算
开平方
开立方
知识结构图
1.16的平方根是( )
A.4 B.±4 C.256 D.±256
2.9的算术平方根是( )
A.3 B.±3 C.-3 D.81
3.8的立方根是( )
A.4 B.±4 C.2 D.±2
4.正数有 个平方根,0有 个平方根,负数
平方根。
5.正数有 个立方根,0有 个立方根,负数有 个立方根。
6.平方根等于本身的数有 ,算术平方根等于它本身的数是 ,立方根等于本身的数有 。
平方根、立方根、实数知多少?
B
A
C
两
一
没有
一
一
一
0
1和0
1、-1和0
7.填空: = ;
= ;
= ;
= ;
= ;
= ;
= ;
= ;
3
0.5
2
3
4
-5
±1
±1/2
8.判断下列说法是否正确:
(1)实数不是有理数就是无理数( )
(2)无限小数都是无理数( )
(3)无理数都是无限小数( )
(4)带根号的数都是无理数( )
(5)两个无理数之和一定是无理数( )
(6)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数( )
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
9.把下列各数分别填入相应的集合内:
算术平方根 平方根 立方根
定义
表示方法
的取值
性质
≥
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
≠
平方根、算数平方根、立方根的区别与联系
若x2=a,则x是a的平方根
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.与数轴上的点一一对应的数是( )
A.有理数 B.无理数 C.实数 D.整数
4. 最小值是 ,此时a的取值是 。
2.估算 的值在整数( )之间
A.1到4 B.1到2 C.3到4 D.2到4
3.如果一个数的平方根是-3,那么它的另一个平方根是 。
C
B
3
2
-1
题组训练
例1:如果一个正数的平方根为a+1和 2a-7,求这个数。
解:由题意得:(a+1)+(2a-7)=0
解得a=2
所以a+1=3,2a-7=-3
所以这个数是9
典例分析
举一反三
1、已知2a-1的平方根是±3,b+1的算术平方根是2,则a= ,b= 。
2、已知x-1的平方根是±4,x+y-1的立方根是2,则x= ,y= 。
5
3
17
-8
例2:已知 与 互为相反数,求(x-2y)2的平方根。
解:因为 与 互为相反数
所以 + =0
所以 x-y+3=0 x=-1
x+y-1=0 解得 y=2
所以(x-2y)2=25, (x-y)2的平方根是±5
典例分析
1、已知 ,求
的值 ;
2、已知 ,求2x+y的立方根。
解(1)由题意得
b-2c-1 =0 b=5
c-2=0 解得 c=2
所以b+2c=9
所以 =3
解(2)由题意得
2x-y=0 x=2
x-2=0 解得 y=4
所以2x+y=8
所以2x+y的立方根是2
拓展提高
例3:求下面各式中的x的值
(1)(x-1)2=4 (2)3(x-3)3-24=0
解:(1)x-1=±2
x-1=2或x-1=-2
x=3或-1
解:(2)3(x-3)3=24
(x-3)3=8
x-3=2
x=5
整体思想、转化思想、分类思想
典例分析
学以致用
1.小明家客厅里5块正方形地砖的面积为32000cm2,求每一块正方形地砖的边长。
2.一块直角三角形的花坛,它的两条直角边c长分别为5m,12m,求它的斜边长。
5
12
课堂聚焦
今日事,今日毕
交流学习心得,体会丰收喜悦
平方根、立方根、实数
数学思想:
分类思想、方程思想、数形结合思想及转化思想。
小结
登高才能望远,才能看到最美的风景;探索才有收获,才能感受到真正的快乐!
愿同学们能够把握知识命脉成为一个快乐的探索者。
!
祝:同学们学习进步,
天天 开心!
1.已知a、b满足b = 则a= ,b= 。
2.已知 的小数部分是a,
的小数部分是b,a= , b= ,a+b的平方根是 。
挑战自我
5
-4
±1
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
