苏科版八年级数学上册4.1平方根第一课时 教学设计
文档属性
| 名称 | 苏科版八年级数学上册4.1平方根第一课时 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 36.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 16:09:08 | ||
图片预览

文档简介
4.1平方根第一课时教学设计
一、教学目标
1.了解平方根的概念,会用根号表示数的平方根;
2.了解开方与乘方互为逆运算,会用平方根运算求某些非负数的平方根.
二、教学重点及难点
重点:了解开方与乘方互为逆运算,能熟练地用平方根求某些非负数的平方根
难点:用平方根运算求某些非负数的平方根.
三、教学过程
(一)问题情境:
1. 4+( )= 1 想:1-4 =?
4×( )=-8 想:- 8÷4 =?
(设计意图:问题情境一学生回顾所学的计算,回忆与领悟到 “减法是加法的逆运算. 除法是乘法的逆运算.”为学习接下来的运算开方与乘方之间的互逆关系打下基础。)
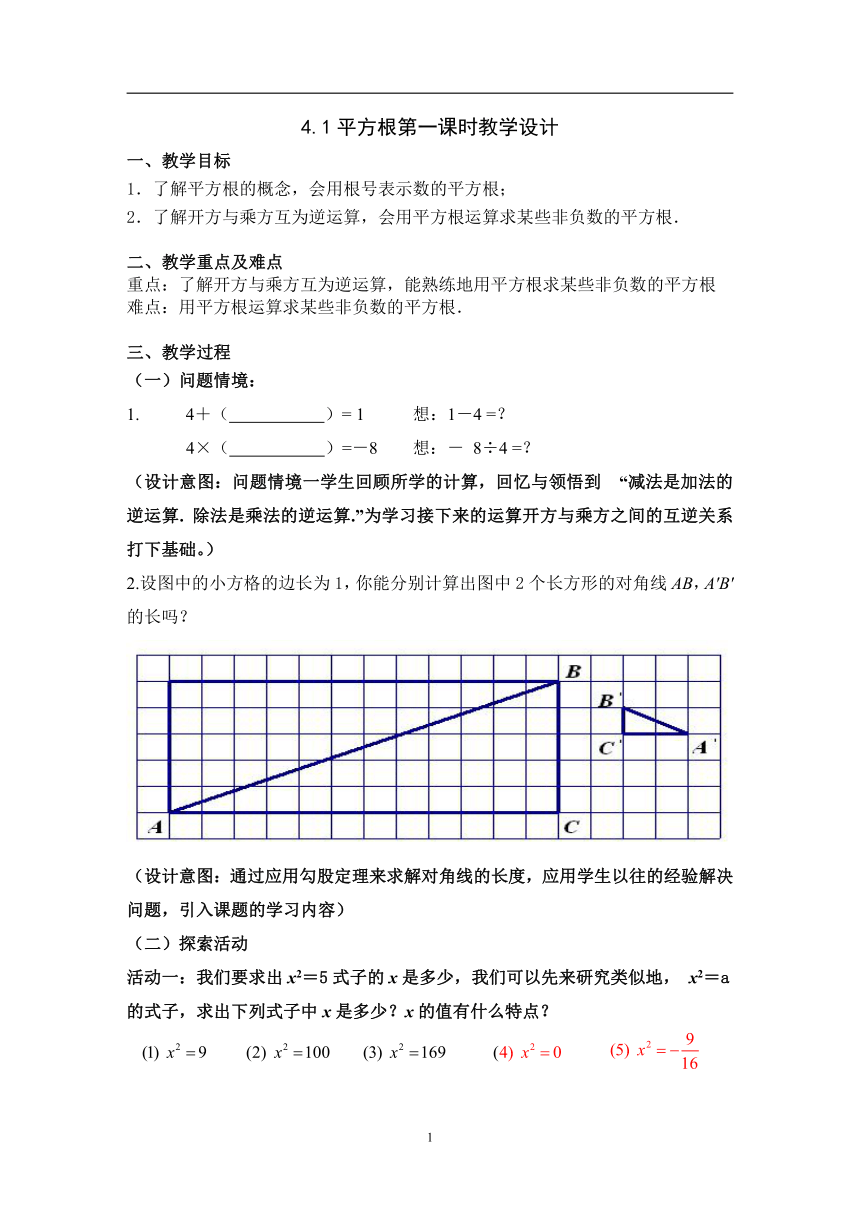
2.设图中的小方格的边长为1,你能分别计算出图中2个长方形的对角线AB,A′B′的长吗?
(设计意图:通过应用勾股定理来求解对角线的长度,应用学生以往的经验解决问题,引入课题的学习内容)
(二)探索活动
活动一:我们要求出x2=5式子的x是多少,我们可以先来研究类似地, x2=a的式子,求出下列式子中x是多少?x的值有什么特点?
活动二:在下列各括号中能填写适当的数使等式成立吗?如果能,请填写;如果不能,请说明理由,并与同学交流.
(2)( )2=9,( )2=5,( )2=;( )2=0,( )2=-9,
(3).请举出与上面类似的例子,你能得到什么结论?
(活动的几个安排的意图:基于平方根概念形成而设计的,通过具体的问题引出概念,再通过学生熟悉的平方运算引导学生关注开平方的运算的特点,然后给出开平方根的概念及符号表示,最后明确概念的内涵,体现了一个概念学习的完整过程。)
(三)、知识归纳与学习:
1.平方根概念:
如果一个数的平方等于a,那么这个数叫做a的平方根,也称为二次方根.也就是说,如果x =a (a≥0),那么x叫做a的平方根。
2.平方根符号的表示和读法
一个正数的平方根有2个,它们互为相反数.一个正数a的正的平方根,记作“ ”.一个正数a的负的平方根,记作“-”.这两个平方根合起来记作“± ”,读作“正、负根号a ”.
例如,2的平方根记作“± ”,读作“正、负根号2”.
81的平方根记作“ ±”,读作“正、负根号81”.
3.平方根性质:
一个正数有两个平方根,它们互为相反数;0的平方根是0;
负数没有平方根.
(初次学习平方根的概念,学生一些困难,可以适当多增加一些例子,从所例举的例子中要对比平方运算和开平方的运算,感受互逆的运算关系)
(四)知识应用与讲解:
1.求下列各数的平方根.
(1)25;(2);(3)15;(4)0.09 (5) 2.25 (6) 0
(联系的选取是在与关注学生们对平方根的概念的理解,通过例题讲解和学生先进行练习,重视学生的基础掌握,和对概念的重点掌握,关注学生正确的使用符号)
2.拓展练习:
(1) x =16 ; (2) x = ;
(3) x =15 ; (4) 4x =81.
(五)解决实际问题
1.你能表示出A′B′ =1 +2 =5,那么A′B′ =?
2.七年级上学期我们曾将两个边长为1的小正方形拼成一个大正方形,这个大正方形面积为2,那么他的边长是多少呢?
(六)课堂小结
1.说说你对平方根的理解.
2.一个正数有两个平方根,它们互为相反数;0只有一个平方根,它是0本身;
负数没有平方根.
求一个数a的平方根的运算,叫做开平方.
由于平方与开平方互为逆运算,因此可以通过平方运算来求一个数的平方根,也可以通过平方运算来检验一个数是不是另一个数的平方根.
(七)课后作业
书本P97习题4.1第1题.第3题.
3
一、教学目标
1.了解平方根的概念,会用根号表示数的平方根;
2.了解开方与乘方互为逆运算,会用平方根运算求某些非负数的平方根.
二、教学重点及难点
重点:了解开方与乘方互为逆运算,能熟练地用平方根求某些非负数的平方根
难点:用平方根运算求某些非负数的平方根.
三、教学过程
(一)问题情境:
1. 4+( )= 1 想:1-4 =?
4×( )=-8 想:- 8÷4 =?
(设计意图:问题情境一学生回顾所学的计算,回忆与领悟到 “减法是加法的逆运算. 除法是乘法的逆运算.”为学习接下来的运算开方与乘方之间的互逆关系打下基础。)
2.设图中的小方格的边长为1,你能分别计算出图中2个长方形的对角线AB,A′B′的长吗?
(设计意图:通过应用勾股定理来求解对角线的长度,应用学生以往的经验解决问题,引入课题的学习内容)
(二)探索活动
活动一:我们要求出x2=5式子的x是多少,我们可以先来研究类似地, x2=a的式子,求出下列式子中x是多少?x的值有什么特点?
活动二:在下列各括号中能填写适当的数使等式成立吗?如果能,请填写;如果不能,请说明理由,并与同学交流.
(2)( )2=9,( )2=5,( )2=;( )2=0,( )2=-9,
(3).请举出与上面类似的例子,你能得到什么结论?
(活动的几个安排的意图:基于平方根概念形成而设计的,通过具体的问题引出概念,再通过学生熟悉的平方运算引导学生关注开平方的运算的特点,然后给出开平方根的概念及符号表示,最后明确概念的内涵,体现了一个概念学习的完整过程。)
(三)、知识归纳与学习:
1.平方根概念:
如果一个数的平方等于a,那么这个数叫做a的平方根,也称为二次方根.也就是说,如果x =a (a≥0),那么x叫做a的平方根。
2.平方根符号的表示和读法
一个正数的平方根有2个,它们互为相反数.一个正数a的正的平方根,记作“ ”.一个正数a的负的平方根,记作“-”.这两个平方根合起来记作“± ”,读作“正、负根号a ”.
例如,2的平方根记作“± ”,读作“正、负根号2”.
81的平方根记作“ ±”,读作“正、负根号81”.
3.平方根性质:
一个正数有两个平方根,它们互为相反数;0的平方根是0;
负数没有平方根.
(初次学习平方根的概念,学生一些困难,可以适当多增加一些例子,从所例举的例子中要对比平方运算和开平方的运算,感受互逆的运算关系)
(四)知识应用与讲解:
1.求下列各数的平方根.
(1)25;(2);(3)15;(4)0.09 (5) 2.25 (6) 0
(联系的选取是在与关注学生们对平方根的概念的理解,通过例题讲解和学生先进行练习,重视学生的基础掌握,和对概念的重点掌握,关注学生正确的使用符号)
2.拓展练习:
(1) x =16 ; (2) x = ;
(3) x =15 ; (4) 4x =81.
(五)解决实际问题
1.你能表示出A′B′ =1 +2 =5,那么A′B′ =?
2.七年级上学期我们曾将两个边长为1的小正方形拼成一个大正方形,这个大正方形面积为2,那么他的边长是多少呢?
(六)课堂小结
1.说说你对平方根的理解.
2.一个正数有两个平方根,它们互为相反数;0只有一个平方根,它是0本身;
负数没有平方根.
求一个数a的平方根的运算,叫做开平方.
由于平方与开平方互为逆运算,因此可以通过平方运算来求一个数的平方根,也可以通过平方运算来检验一个数是不是另一个数的平方根.
(七)课后作业
书本P97习题4.1第1题.第3题.
3
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
