2021-2022学年人教版四年级数学上册《1.2 数的产生》同步练习题(含答案)
文档属性
| 名称 | 2021-2022学年人教版四年级数学上册《1.2 数的产生》同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 19:49:37 | ||
图片预览



文档简介
2021-2022学年人教版四年级数学上册《1.2 数的产生》同步练习
一、单选题
1.最小的自然数是( )
A.0 B.1 C.2
2.下列说法正确的是( )
A.自然数都是整数
B.小数的末尾加上0,小数变小
C.0.75000比75%小
3.15个连续自然数的和( )
A.是奇数
B.是偶数
C.可能是奇数,也可能是偶数
二、判断题
4.没有最大的自然数. .(判断对错)
5.自然数都比0大 .
6.如果a是不为0的自然数,则与a相邻的两个自然数分别是a﹣1和a+1. (判断对错)
7.所有的自然数都是整数. (判断对错)
三、填空题
8.表示物体个数的1,2,3,…都是 数,这种数的个数是 .
9.有一个六位数,加上1就变成七位数,这个六位数是 。
10.比最小的八位数少1的数是 ,比最大的六位数多1的数是 。
11.三个连续的自然数的中间的一个为a,这三个自然数的和是 .
四、解答题
12.请把小学学过的数整理画成图表示出来.
13.—个数是150和250之间的一个自然数,且比18的倍数多3,这个数最大是多少?
五、应用题
14.军军、朋朋和奇奇三个小朋友的年龄是三个连续的自然数,且积是720。这三个小朋友的年龄分别是多少?
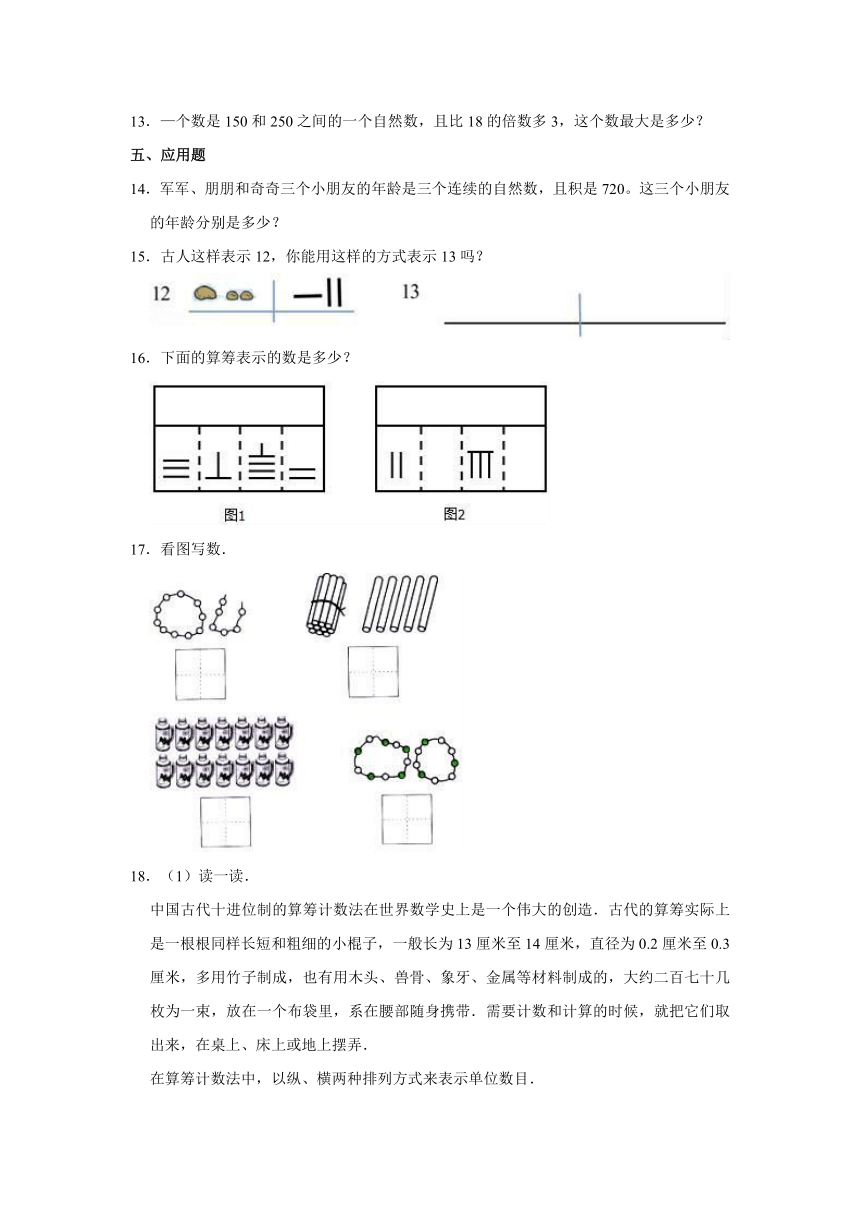
15.古人这样表示12,你能用这样的方式表示13吗?
16.下面的算筹表示的数是多少?
17.看图写数.
18.(1)读一读.
中国古代十进位制的算筹计数法在世界数学史上是一个伟大的创造.古代的算筹实际上是一根根同样长短和粗细的小棍子,一般长为13厘米至14厘米,直径为0.2厘米至0.3厘米,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要计数和计算的时候,就把它们取出来,在桌上、床上或地上摆弄.
在算筹计数法中,以纵、横两种排列方式来表示单位数目.
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空.例如:137表示为,32591表示为.
(2)用算筹计数法表示下列各数.
24 .
1832 .
33 .
32051 .
(3)写出下列用算筹计数法表示的数.
参考答案与试题解析
一、单选题
1.【分析】一个物体也没有,用0表示,0也是自然数,0是最小的自然数.自然数的个数是无限的,所以没有最大的自然数.据此解答即可.
【解答】解:最小的自然数是0;
故选:A.
【点评】此题考查了自然数的概念,现行教材中都规定0为自然数,即非负整数都是自然数.
2.【分析】根据题意,对各选项进行依次分析、进而得出结论。
【解答】解:A、自然数都是整数,说法正确,整数包括正数、负数、0,所有的自然数都是整数;
B、小数的末尾加上0,小数变小,说法错误,小数的末尾加上0,小数大小不变;
C、0.75000比75%小,说法错误,它们相等。
故选:A。
【点评】此题涉及的知识点较多,但比较简单,只有认真,容易完成,注意平时基础知识的积累。
3.【分析】所有的偶数的和都是偶数,奇数个奇数的和是奇数,偶数个奇数的和是偶数;由此根据自然数的特征判断即可。
【解答】解:15个连续自然数可能有7个奇数和8个偶数,这样和就是奇数;如果有8个奇数和7个偶数,那么和就是偶数,所以15个连续自然数的和可能是奇数,也可能是偶数。
故选:C。
【点评】明确奇数和偶数的性质,是解答此题的关键。
二、判断题
4.【分析】根据自然数的意义:表示物体个数的1、2、3、4、5、6、7、8、9、10、11,…都是自然数,一个物体也没有用0表示. 0也是自然数,最小的自然数是0,没有最大的自然数,自然数的个数是无限的.
【解答】解:没有最大的自然数,自然数的个数是无限的.所以题干说法正确.
故答案为:√.
【点评】本题主要考查自然数的意义,注意最小的自然数是0,没有最大的自然数,自然数的个数是无限的.
5.【分析】根据自然数的含义:用以计量事物的件数或表示事物次序的数,即用数码0,1,2,3,4,…所表示的数;自然数由0开始(包括0),一个接一个,组成一个无穷的集体;据此判断即可.
【解答】解:由自然数的含义可知:自然数都大于零不对,因为零也是自然数;
故答案为:×.
【点评】此题考查了自然数的含义,应明确最小的自然数为0.
6.【分析】因为相邻的两个自然数相差1,则与a相邻的两个自然数为:a﹣1,a+1;据此解答即可.
【解答】解:a是一个不为0自然数,与a相邻的两个自然数分别a﹣1、a+1,说法正确;
故答案为:√.
【点评】解答此题的关键是知道每相邻的两个自然数之间相差1.
7.【分析】整数包括自然数和负整数,自然数都是整数,整数包括自然数,自然数是整数的一部分.
【解答】解:由分析可知,自然数都是整数,
此题说法正确;
故答案为:√.
【点评】此题考查了对整数的认识.
三、填空题
8.【分析】根据自然数的意义:表示物体个数的1、2、3、4、5、6、7、8、9、10、11,…都是自然数,一个物体也没有用0表示,0也是自然数,最小的自然数是0,没有最大的自然数,自然数的个数是无限的.据此解答即可.
【解答】解:表示物体个数的1,2,3,…都是 自然数,这种数的个数是 无限的;
故答案为:自然,无限的.
【点评】本题主要考查自然数的意义,注意自然数的个数是无限的.
9.【分析】相邻的自然数相差1,最大的六位数999999加上1之后就会变成最小的七位数1000000。
【解答】解:999999+1=1000000
所以六位数加上1变成七位数,这个六位数是999999。
故答案为:999999。
【点评】本题根据最大的六位数与最小的七位数之间相差1直接求解。
10.【分析】最小的八位数是10000000,求比最小的八位数少1的数,用10000000﹣1;
最大的六位数是999999,求比最大的六位数多1的数,用999999+1。
【解答】解:10000000﹣1=9999999
所以比最小的八位数少1的数是9999999;
999999+1=1000000
所以比最大的六位数多1的数是1000000。
故答案为:9999999,1000000。
【点评】此题考查了整数的认识,最小的八位数是10000000,最大的六位数是999999。
11.【分析】由已知,三个连续自然数之间的关系是依次大1,由此表示出三个连续自然数为:a﹣1,a,a+1.然后求和.
【解答】解:因为已知三个连续自然数且中间一个为a,所以另两个为:a﹣1,a+1.
则三个连续自然数的和为:a﹣1+a+a+1=3a.
故答案为:3a.
【点评】此题考查了学生对列代数式这个知识点的理解与掌握,解此题的关键是据三个连续自然数的关系先列出代数式,再求和.
四、解答题
12.【分析】根据数的分类即可求解.
【解答】解:分类如下:
【点评】考查了整数的认识,小数和分数的分类,是基础题型.
13.【分析】按最大的250除以18,得出的商乘18倍再加上3,就是所求的数。
【解答】解:250÷18=13……16
18×13+3=237
答:这个数最大的是237。
【点评】解答本题的关键是知道按最大的250除以18,得出的商。然后再解答。
五、应用题
14.【分析】相邻的自然数的差是1,由此判断出三个连续自然数的积是720的数,这三个自然数就是三个小朋友的年龄。
【解答】解:因为720=8×9×10,
所以,这三个小朋友的年龄分别是8岁,9岁,10岁。
答:这三个小朋友的年龄分别是8岁,9岁,10岁。
【点评】解答本题关键是明确相邻的自然数的差是1.
15.【分析】12里有1个十,2个一,1块大石头表示一个十,2块小石头表示2个一,横放1根木枝表示1个十,竖放2根木枝表示2个一,据此可知,因为13里有1个十,3个一,所以放1块大石头表示一个十,3块小石头表示3个一,横放1根木枝表示1个十,竖放3根木枝表示3个一。
【解答】解:
【点评】此题重点考查两位数的组成和观察能力。
16.【分析】算筹的计数方法是:横式中一“竖”表示1、二“竖”表示2、三“竖”表示3…一“横”表示5;“纵式中一“横”表示1、二“横”表示2,三“横”表示3…一“竖”表示5.“横”“竖”结合,所表示的数相加.
【解答】解:如图
图1所表示的数是3692,图2表2080.
【点评】此题是考查算筹表示数的方法,关键是记住每种符号所表示的意义.
17.【分析】数一数即可解答,①一串有10个珠子,再加上6个珠子,共有16个珠子;
②1捆有10根小棒,再加上5根,共有15根小棒;
③1行有7个暖瓶,两行共有14个暖瓶;
④1串有10个珠子,再加上另一串9个珠子,共有19个珠子;即可得解.
【解答】解:
【点评】此题锻炼了学生的数数能力,以及数的写法.
18.【分析】根据题意可知算筹计数法也是十进制的,表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空;由此解答即可.
【解答】解:(1)算筹计数法也是十进制的,表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空;
(2)用算筹计数法表示下列各数.
24表示:;
1832表示:;
33表示:;
32051表示:;
(3)写出下列用算筹计数法表示的数.
表示:51;
表示:42658;
表示:565;
表示:837924.
故答案为:,,,;51,42658,565,837924.
【点评】考查了应用类问题,关键是对我国古代用算筹记数的规定的理解和掌握.
一、单选题
1.最小的自然数是( )
A.0 B.1 C.2
2.下列说法正确的是( )
A.自然数都是整数
B.小数的末尾加上0,小数变小
C.0.75000比75%小
3.15个连续自然数的和( )
A.是奇数
B.是偶数
C.可能是奇数,也可能是偶数
二、判断题
4.没有最大的自然数. .(判断对错)
5.自然数都比0大 .
6.如果a是不为0的自然数,则与a相邻的两个自然数分别是a﹣1和a+1. (判断对错)
7.所有的自然数都是整数. (判断对错)
三、填空题
8.表示物体个数的1,2,3,…都是 数,这种数的个数是 .
9.有一个六位数,加上1就变成七位数,这个六位数是 。
10.比最小的八位数少1的数是 ,比最大的六位数多1的数是 。
11.三个连续的自然数的中间的一个为a,这三个自然数的和是 .
四、解答题
12.请把小学学过的数整理画成图表示出来.
13.—个数是150和250之间的一个自然数,且比18的倍数多3,这个数最大是多少?
五、应用题
14.军军、朋朋和奇奇三个小朋友的年龄是三个连续的自然数,且积是720。这三个小朋友的年龄分别是多少?
15.古人这样表示12,你能用这样的方式表示13吗?
16.下面的算筹表示的数是多少?
17.看图写数.
18.(1)读一读.
中国古代十进位制的算筹计数法在世界数学史上是一个伟大的创造.古代的算筹实际上是一根根同样长短和粗细的小棍子,一般长为13厘米至14厘米,直径为0.2厘米至0.3厘米,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要计数和计算的时候,就把它们取出来,在桌上、床上或地上摆弄.
在算筹计数法中,以纵、横两种排列方式来表示单位数目.
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空.例如:137表示为,32591表示为.
(2)用算筹计数法表示下列各数.
24 .
1832 .
33 .
32051 .
(3)写出下列用算筹计数法表示的数.
参考答案与试题解析
一、单选题
1.【分析】一个物体也没有,用0表示,0也是自然数,0是最小的自然数.自然数的个数是无限的,所以没有最大的自然数.据此解答即可.
【解答】解:最小的自然数是0;
故选:A.
【点评】此题考查了自然数的概念,现行教材中都规定0为自然数,即非负整数都是自然数.
2.【分析】根据题意,对各选项进行依次分析、进而得出结论。
【解答】解:A、自然数都是整数,说法正确,整数包括正数、负数、0,所有的自然数都是整数;
B、小数的末尾加上0,小数变小,说法错误,小数的末尾加上0,小数大小不变;
C、0.75000比75%小,说法错误,它们相等。
故选:A。
【点评】此题涉及的知识点较多,但比较简单,只有认真,容易完成,注意平时基础知识的积累。
3.【分析】所有的偶数的和都是偶数,奇数个奇数的和是奇数,偶数个奇数的和是偶数;由此根据自然数的特征判断即可。
【解答】解:15个连续自然数可能有7个奇数和8个偶数,这样和就是奇数;如果有8个奇数和7个偶数,那么和就是偶数,所以15个连续自然数的和可能是奇数,也可能是偶数。
故选:C。
【点评】明确奇数和偶数的性质,是解答此题的关键。
二、判断题
4.【分析】根据自然数的意义:表示物体个数的1、2、3、4、5、6、7、8、9、10、11,…都是自然数,一个物体也没有用0表示. 0也是自然数,最小的自然数是0,没有最大的自然数,自然数的个数是无限的.
【解答】解:没有最大的自然数,自然数的个数是无限的.所以题干说法正确.
故答案为:√.
【点评】本题主要考查自然数的意义,注意最小的自然数是0,没有最大的自然数,自然数的个数是无限的.
5.【分析】根据自然数的含义:用以计量事物的件数或表示事物次序的数,即用数码0,1,2,3,4,…所表示的数;自然数由0开始(包括0),一个接一个,组成一个无穷的集体;据此判断即可.
【解答】解:由自然数的含义可知:自然数都大于零不对,因为零也是自然数;
故答案为:×.
【点评】此题考查了自然数的含义,应明确最小的自然数为0.
6.【分析】因为相邻的两个自然数相差1,则与a相邻的两个自然数为:a﹣1,a+1;据此解答即可.
【解答】解:a是一个不为0自然数,与a相邻的两个自然数分别a﹣1、a+1,说法正确;
故答案为:√.
【点评】解答此题的关键是知道每相邻的两个自然数之间相差1.
7.【分析】整数包括自然数和负整数,自然数都是整数,整数包括自然数,自然数是整数的一部分.
【解答】解:由分析可知,自然数都是整数,
此题说法正确;
故答案为:√.
【点评】此题考查了对整数的认识.
三、填空题
8.【分析】根据自然数的意义:表示物体个数的1、2、3、4、5、6、7、8、9、10、11,…都是自然数,一个物体也没有用0表示,0也是自然数,最小的自然数是0,没有最大的自然数,自然数的个数是无限的.据此解答即可.
【解答】解:表示物体个数的1,2,3,…都是 自然数,这种数的个数是 无限的;
故答案为:自然,无限的.
【点评】本题主要考查自然数的意义,注意自然数的个数是无限的.
9.【分析】相邻的自然数相差1,最大的六位数999999加上1之后就会变成最小的七位数1000000。
【解答】解:999999+1=1000000
所以六位数加上1变成七位数,这个六位数是999999。
故答案为:999999。
【点评】本题根据最大的六位数与最小的七位数之间相差1直接求解。
10.【分析】最小的八位数是10000000,求比最小的八位数少1的数,用10000000﹣1;
最大的六位数是999999,求比最大的六位数多1的数,用999999+1。
【解答】解:10000000﹣1=9999999
所以比最小的八位数少1的数是9999999;
999999+1=1000000
所以比最大的六位数多1的数是1000000。
故答案为:9999999,1000000。
【点评】此题考查了整数的认识,最小的八位数是10000000,最大的六位数是999999。
11.【分析】由已知,三个连续自然数之间的关系是依次大1,由此表示出三个连续自然数为:a﹣1,a,a+1.然后求和.
【解答】解:因为已知三个连续自然数且中间一个为a,所以另两个为:a﹣1,a+1.
则三个连续自然数的和为:a﹣1+a+a+1=3a.
故答案为:3a.
【点评】此题考查了学生对列代数式这个知识点的理解与掌握,解此题的关键是据三个连续自然数的关系先列出代数式,再求和.
四、解答题
12.【分析】根据数的分类即可求解.
【解答】解:分类如下:
【点评】考查了整数的认识,小数和分数的分类,是基础题型.
13.【分析】按最大的250除以18,得出的商乘18倍再加上3,就是所求的数。
【解答】解:250÷18=13……16
18×13+3=237
答:这个数最大的是237。
【点评】解答本题的关键是知道按最大的250除以18,得出的商。然后再解答。
五、应用题
14.【分析】相邻的自然数的差是1,由此判断出三个连续自然数的积是720的数,这三个自然数就是三个小朋友的年龄。
【解答】解:因为720=8×9×10,
所以,这三个小朋友的年龄分别是8岁,9岁,10岁。
答:这三个小朋友的年龄分别是8岁,9岁,10岁。
【点评】解答本题关键是明确相邻的自然数的差是1.
15.【分析】12里有1个十,2个一,1块大石头表示一个十,2块小石头表示2个一,横放1根木枝表示1个十,竖放2根木枝表示2个一,据此可知,因为13里有1个十,3个一,所以放1块大石头表示一个十,3块小石头表示3个一,横放1根木枝表示1个十,竖放3根木枝表示3个一。
【解答】解:
【点评】此题重点考查两位数的组成和观察能力。
16.【分析】算筹的计数方法是:横式中一“竖”表示1、二“竖”表示2、三“竖”表示3…一“横”表示5;“纵式中一“横”表示1、二“横”表示2,三“横”表示3…一“竖”表示5.“横”“竖”结合,所表示的数相加.
【解答】解:如图
图1所表示的数是3692,图2表2080.
【点评】此题是考查算筹表示数的方法,关键是记住每种符号所表示的意义.
17.【分析】数一数即可解答,①一串有10个珠子,再加上6个珠子,共有16个珠子;
②1捆有10根小棒,再加上5根,共有15根小棒;
③1行有7个暖瓶,两行共有14个暖瓶;
④1串有10个珠子,再加上另一串9个珠子,共有19个珠子;即可得解.
【解答】解:
【点评】此题锻炼了学生的数数能力,以及数的写法.
18.【分析】根据题意可知算筹计数法也是十进制的,表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空;由此解答即可.
【解答】解:(1)算筹计数法也是十进制的,表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空;
(2)用算筹计数法表示下列各数.
24表示:;
1832表示:;
33表示:;
32051表示:;
(3)写出下列用算筹计数法表示的数.
表示:51;
表示:42658;
表示:565;
表示:837924.
故答案为:,,,;51,42658,565,837924.
【点评】考查了应用类问题,关键是对我国古代用算筹记数的规定的理解和掌握.
