2021-2022学年人教版数学八年级上册12.3 角的平分线的性质和判定--综合运用课件(17张ppt)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册12.3 角的平分线的性质和判定--综合运用课件(17张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 428.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
12.3角的平分线的性质和判定的综合运用
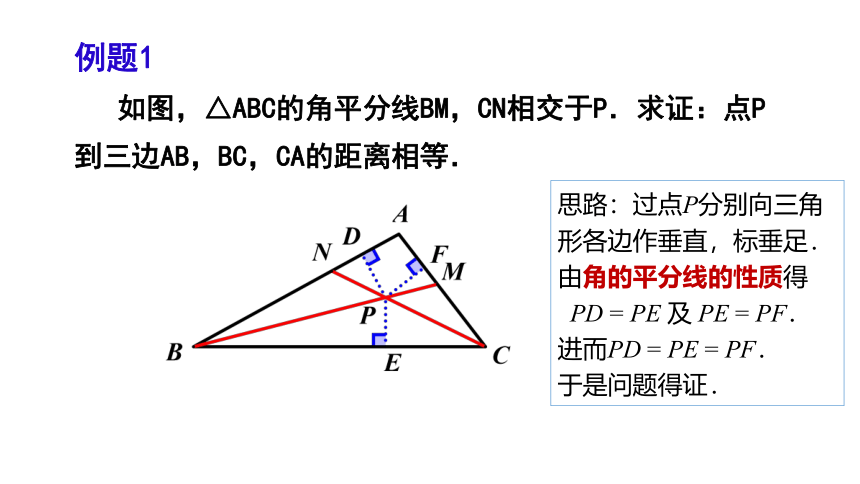
角的平分线的性质和判定回顾对比
图形语言
文字语言 应用格式
主要作用
P
C
P
C
因为PD=PE
PD⊥OA于D
PE⊥OB于E
所以OP平分∠AOB
因为OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
所以PD=PE
证明线段PD=PE相等
判断OC是不是角平分线
代替用全等证明线段相等
除定义外判断角平分线的方法
例题1
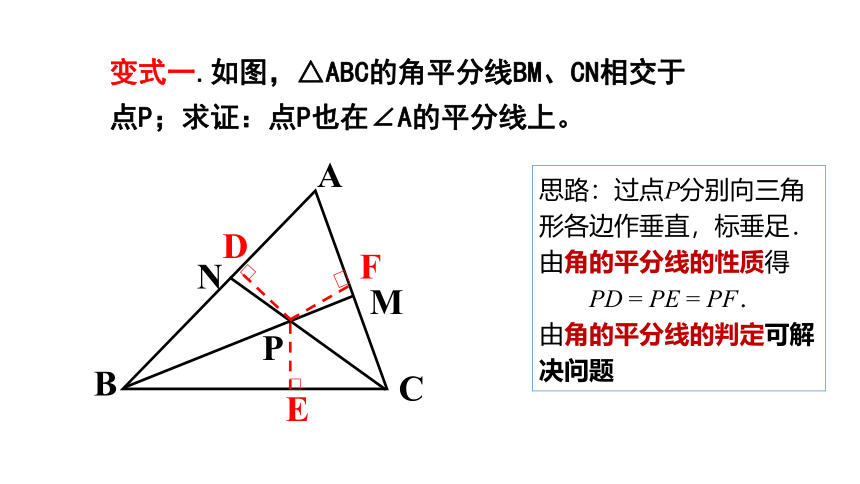
如图,△ABC的角平分线BM,CN相交于P.求证:点P到三边AB,BC,CA的距离相等.
思路:过点P分别向三角形各边作垂直,标垂足.
由角的平分线的性质得
PD = PE 及 PE = PF.
进而PD = PE = PF.
于是问题得证.
A
B
C
P
E
D
F
M
N
变式一.如图,△ABC的角平分线BM、CN相交于点P;求证:点P也在∠A的平分线上。
思路:过点P分别向三角形各边作垂直,标垂足.
由角的平分线的性质得
PD = PE = PF.
由角的平分线的判定可解决问题
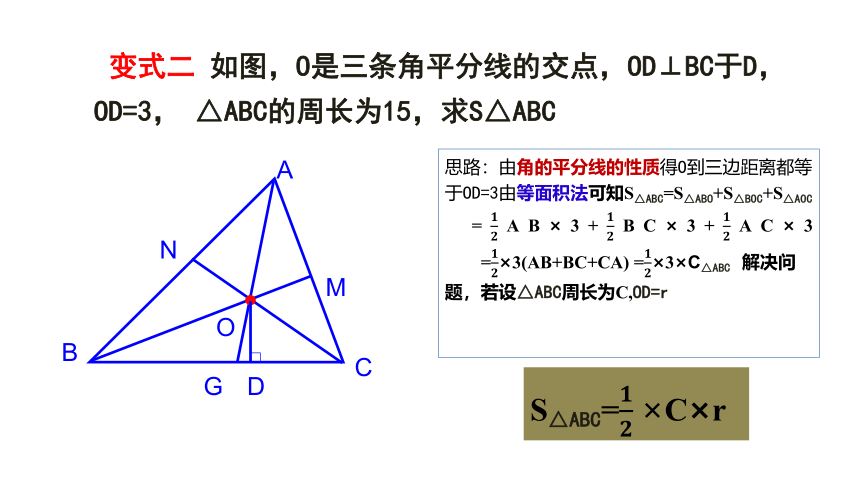
变式二 如图,O是三条角平分线的交点,OD⊥BC于D,OD=3, △ABC的周长为15,求S△ABC
A
B
C
O
M
N
G
D
S△ABC=C×r
思路:由角的平分线的性质得O到三边距离都等于OD=3由等面积法可知S△ABC=S△ABO+S△BOC+S△AOC
=AB×3+BC×3+AC×3
=×3(AB+BC+CA) =×3×C△ABC 解决问题,若设△ABC周长为C,OD=r
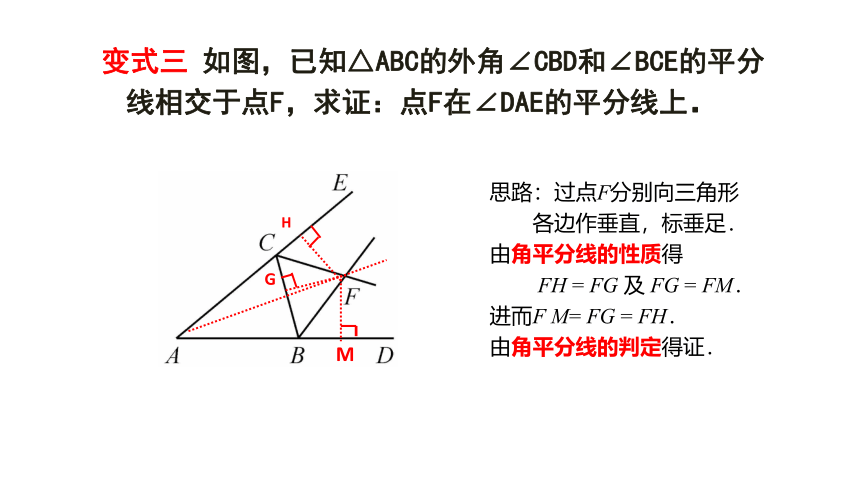
变式三 如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
H
M
G
思路:过点F分别向三角形
各边作垂直,标垂足.
由角平分线的性质得
FH = FG 及 FG = FM.
进而F M= FG = FH.
由角平分线的判定得证.
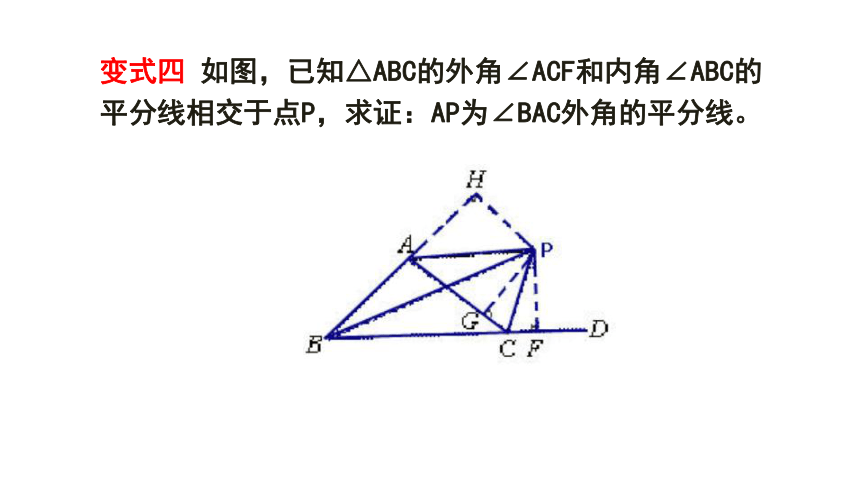
变式四 如图,已知△ABC的外角∠ACF和内角∠ABC的平分线相交于点P,求证:AP为∠BAC外角的平分线。
例题2
如图,为了促进当地旅游发展,某地要在三条互相交叉公路的S区修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
S
作图思路:
分别作∠BAC和∠ABC的平分线,
两线交于点O,
则点O即为所求.
可以试试证明.
变式一 如图,为了促进当地旅游发展,某地要在三条互相交叉公路的S1区修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
.
S
S1
变式二 如图,为了促进当地旅游发展,某地要在三条互相交叉公路的S2区修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
.
S
S1
S2
变式三 如图,为了促进当地旅游发展,某地要在三条互相交叉公路的S3区修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
.
S
S1
S2
S3
变式四 如图,为了促进当地旅游发展,某地要在三条互相交叉公路所在平面区域修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
.
S
S1
S2
S3
例题3
如图,在△ABC中,点D,E,F在边BC上,点P在线段AD上,若PE∥AB,PF∥AC,点D到PE和PF的距离相等.求证:点D到AB和AC的距离相等.
证明角平分线思路:
①角平分线判定
②定义.
变式一 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.F是OC上另一点,连接DF,EF.求证:DF = EF.
注意鉴别易混定理.
证法一.证两次全等
证法二.证一次全等
课后小结
1.需注意区分性质和判定的条件和结论,以 免发生混淆.
2.角平分线常见的辅助线:以补全基本图中角平分线上点到两边垂线段为主要辅助线.
3.角平分线证明思路不仅仅是判定,还有定义
1.如图,△ABC的角平分线AP和外角平分线BP相交于点P,求证:点P也在∠BCD的平分线上.
课后练习
2.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF交AD于点G,AD与EF垂直吗?证明你的结论.
12.3角的平分线的性质和判定的综合运用
角的平分线的性质和判定回顾对比
图形语言
文字语言 应用格式
主要作用
P
C
P
C
因为PD=PE
PD⊥OA于D
PE⊥OB于E
所以OP平分∠AOB
因为OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
所以PD=PE
证明线段PD=PE相等
判断OC是不是角平分线
代替用全等证明线段相等
除定义外判断角平分线的方法
例题1
如图,△ABC的角平分线BM,CN相交于P.求证:点P到三边AB,BC,CA的距离相等.
思路:过点P分别向三角形各边作垂直,标垂足.
由角的平分线的性质得
PD = PE 及 PE = PF.
进而PD = PE = PF.
于是问题得证.
A
B
C
P
E
D
F
M
N
变式一.如图,△ABC的角平分线BM、CN相交于点P;求证:点P也在∠A的平分线上。
思路:过点P分别向三角形各边作垂直,标垂足.
由角的平分线的性质得
PD = PE = PF.
由角的平分线的判定可解决问题
变式二 如图,O是三条角平分线的交点,OD⊥BC于D,OD=3, △ABC的周长为15,求S△ABC
A
B
C
O
M
N
G
D
S△ABC=C×r
思路:由角的平分线的性质得O到三边距离都等于OD=3由等面积法可知S△ABC=S△ABO+S△BOC+S△AOC
=AB×3+BC×3+AC×3
=×3(AB+BC+CA) =×3×C△ABC 解决问题,若设△ABC周长为C,OD=r
变式三 如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
H
M
G
思路:过点F分别向三角形
各边作垂直,标垂足.
由角平分线的性质得
FH = FG 及 FG = FM.
进而F M= FG = FH.
由角平分线的判定得证.
变式四 如图,已知△ABC的外角∠ACF和内角∠ABC的平分线相交于点P,求证:AP为∠BAC外角的平分线。
例题2
如图,为了促进当地旅游发展,某地要在三条互相交叉公路的S区修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
S
作图思路:
分别作∠BAC和∠ABC的平分线,
两线交于点O,
则点O即为所求.
可以试试证明.
变式一 如图,为了促进当地旅游发展,某地要在三条互相交叉公路的S1区修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
.
S
S1
变式二 如图,为了促进当地旅游发展,某地要在三条互相交叉公路的S2区修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
.
S
S1
S2
变式三 如图,为了促进当地旅游发展,某地要在三条互相交叉公路的S3区修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
.
S
S1
S2
S3
变式四 如图,为了促进当地旅游发展,某地要在三条互相交叉公路所在平面区域修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
.
S
S1
S2
S3
例题3
如图,在△ABC中,点D,E,F在边BC上,点P在线段AD上,若PE∥AB,PF∥AC,点D到PE和PF的距离相等.求证:点D到AB和AC的距离相等.
证明角平分线思路:
①角平分线判定
②定义.
变式一 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.F是OC上另一点,连接DF,EF.求证:DF = EF.
注意鉴别易混定理.
证法一.证两次全等
证法二.证一次全等
课后小结
1.需注意区分性质和判定的条件和结论,以 免发生混淆.
2.角平分线常见的辅助线:以补全基本图中角平分线上点到两边垂线段为主要辅助线.
3.角平分线证明思路不仅仅是判定,还有定义
1.如图,△ABC的角平分线AP和外角平分线BP相交于点P,求证:点P也在∠BCD的平分线上.
课后练习
2.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF交AD于点G,AD与EF垂直吗?证明你的结论.
