沪教版(上海)数学高二下册-12.8抛物线的性质(教案)
文档属性
| 名称 | 沪教版(上海)数学高二下册-12.8抛物线的性质(教案) |
|
|
| 格式 | doc | ||
| 文件大小 | 128.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:16:22 | ||
图片预览

文档简介
抛物线的性质
【教学目标】
1.理解抛物线的性质;
2.由抛物线的图像和抛物线标准方程,类比椭圆、双曲线的性质的研究方法来探索抛物线的性质;
3.培养学生的严谨的数学思维和探索问题的能力,培养学生数形结合的思想和方法。
【教学重难点】
1.抛物线的性质;
2.利用抛物线的性质来解决简单的实际问题。
【教学过程】
一、复习导入。
1.抛物线的定义;
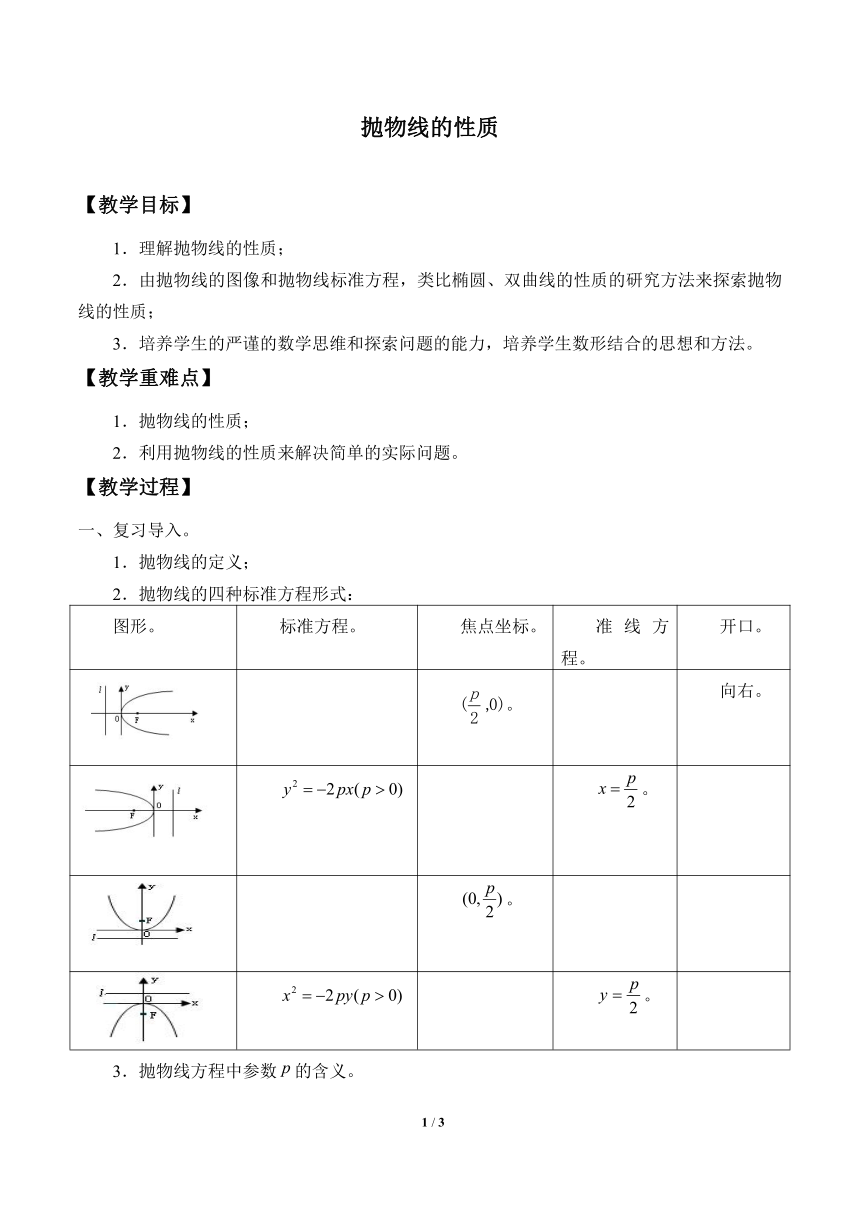
2.抛物线的四种标准方程形式:
图形。 标准方程。 焦点坐标。 准线方程。 开口。
。 向右。
。
。
。
3.抛物线方程中参数的含义。
4.练习:
(1)以(1,0)为焦点的抛物线标准方程为______________。
(2)抛物线的准线方程为______________。
二、新课探究。
我们根据抛物线的标准方程和图像来探索抛物线的性质。
1.对称性。
通过观察图形,可得抛物线的部分图像是关于y轴对称的,那么当x值增大时呢?我们可以由抛物线的方程判断:
在方程中,以代替,方程不变,这表明:如果某点在抛物线上,那么该点关于轴的对称的点也在该抛物线上,即抛物线关于轴对称,它是一轴对称图形。
2.顶点。
由图可得:抛物线与对称轴相交于O点,称O为抛物线的顶点,O也是坐标原点。
3.范围。
由图可得,抛物线的图像除了原点之外都在y轴的右侧,由抛物线的方程可得:
在方程中,因为,所以,这表明除了顶点,抛物线的图像全部落在轴的右侧,在第一象限,随着的增大,抛物线的图像向右上方无限延伸;在第四象限,随着的增大,抛物线的图像向右下方无限延伸。
抛物线的其他三种类型:的性质可以通过类比性质来探索。
【作业布置】
1.求以坐标原点为顶点,交点在坐标轴上且经过点的抛物线的方程。
2.求过定点M(0,1)且与抛物线只有一个公共点的直线的方程。
PAGE
1 / 1
【教学目标】
1.理解抛物线的性质;
2.由抛物线的图像和抛物线标准方程,类比椭圆、双曲线的性质的研究方法来探索抛物线的性质;
3.培养学生的严谨的数学思维和探索问题的能力,培养学生数形结合的思想和方法。
【教学重难点】
1.抛物线的性质;
2.利用抛物线的性质来解决简单的实际问题。
【教学过程】
一、复习导入。
1.抛物线的定义;
2.抛物线的四种标准方程形式:
图形。 标准方程。 焦点坐标。 准线方程。 开口。
。 向右。
。
。
。
3.抛物线方程中参数的含义。
4.练习:
(1)以(1,0)为焦点的抛物线标准方程为______________。
(2)抛物线的准线方程为______________。
二、新课探究。
我们根据抛物线的标准方程和图像来探索抛物线的性质。
1.对称性。
通过观察图形,可得抛物线的部分图像是关于y轴对称的,那么当x值增大时呢?我们可以由抛物线的方程判断:
在方程中,以代替,方程不变,这表明:如果某点在抛物线上,那么该点关于轴的对称的点也在该抛物线上,即抛物线关于轴对称,它是一轴对称图形。
2.顶点。
由图可得:抛物线与对称轴相交于O点,称O为抛物线的顶点,O也是坐标原点。
3.范围。
由图可得,抛物线的图像除了原点之外都在y轴的右侧,由抛物线的方程可得:
在方程中,因为,所以,这表明除了顶点,抛物线的图像全部落在轴的右侧,在第一象限,随着的增大,抛物线的图像向右上方无限延伸;在第四象限,随着的增大,抛物线的图像向右下方无限延伸。
抛物线的其他三种类型:的性质可以通过类比性质来探索。
【作业布置】
1.求以坐标原点为顶点,交点在坐标轴上且经过点的抛物线的方程。
2.求过定点M(0,1)且与抛物线只有一个公共点的直线的方程。
PAGE
1 / 1
