沪教版(上海)数学高二下册-11.4点到直线的距离(1)(课件)(共26张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二下册-11.4点到直线的距离(1)(课件)(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 843.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:19:04 | ||
图片预览

文档简介
(共26张PPT)
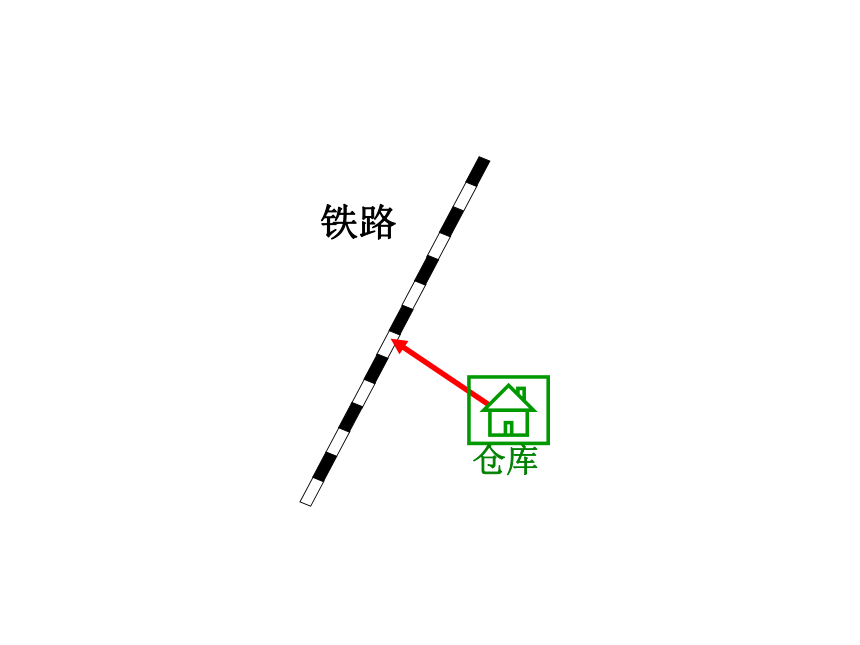
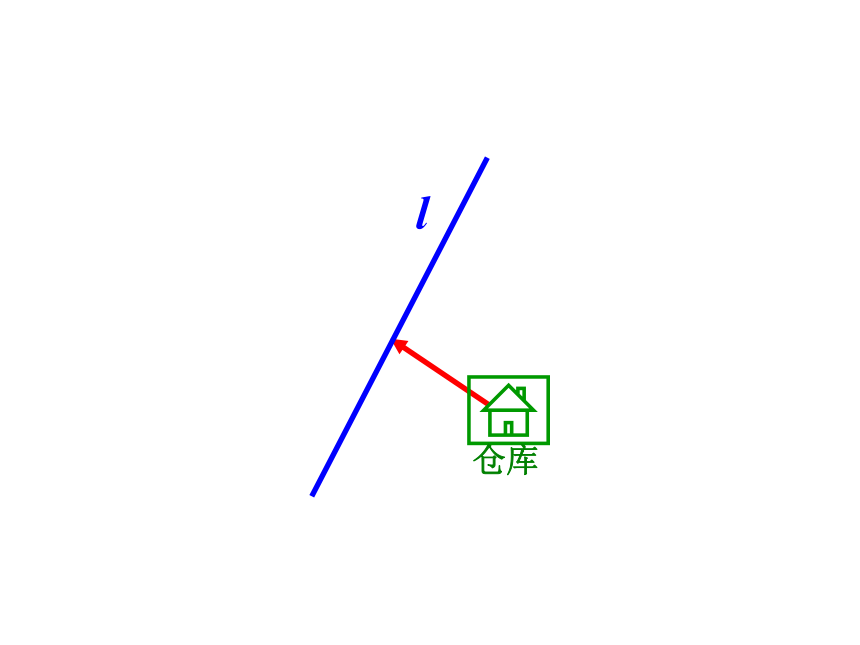
仓库
铁路
仓库
l
.
P
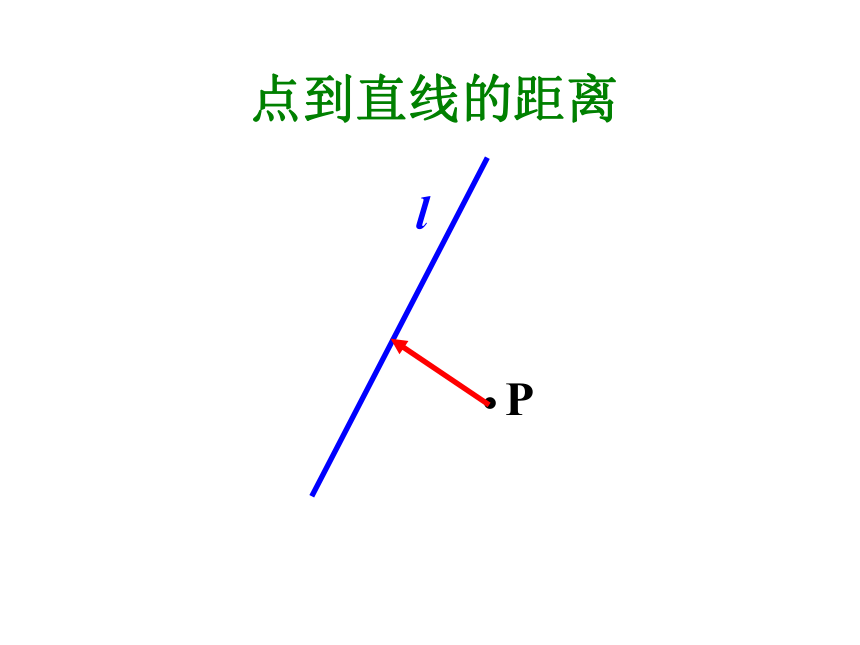
点到直线的距离
l
l
P
.
o
x
y
: Ax+By+C=0
(x0,y0)
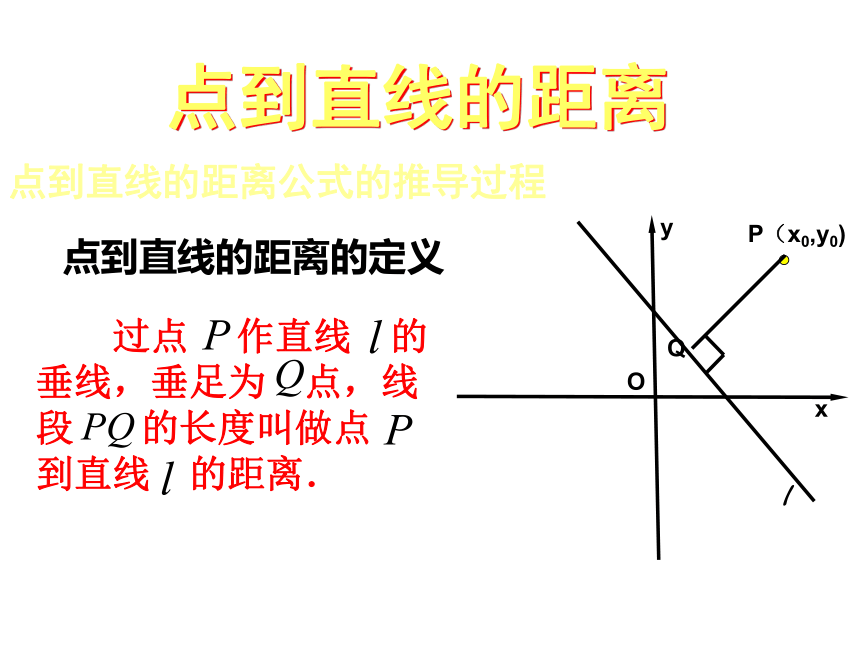
点到直线的距离
点到直线的距离
x
y
O
l
P(x0,y0)
Q
点到直线的距离的定义
点到直线的距离公式的推导过程
过点 作直线 的垂线,垂足为 点,线段 的长度叫做点 到直线 的距离.
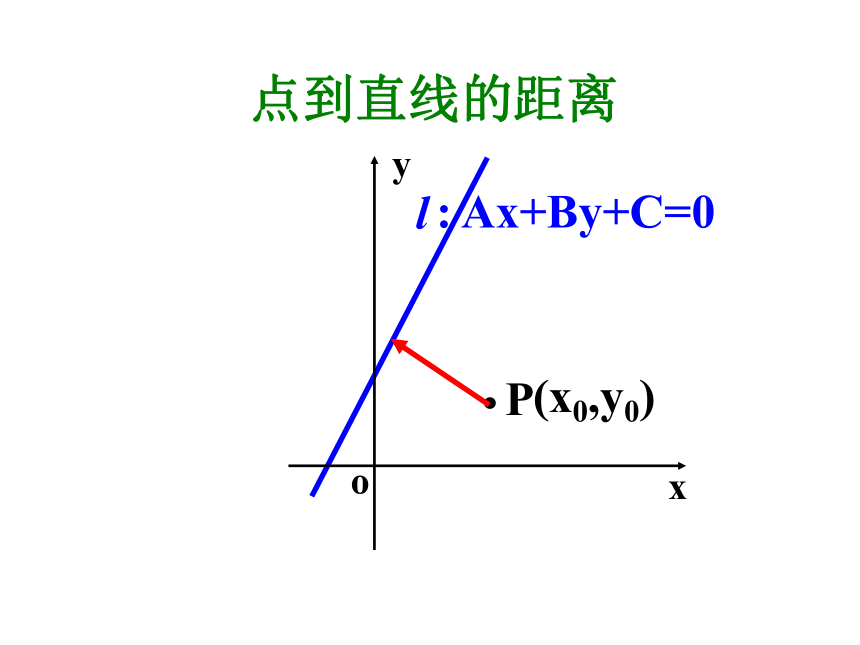
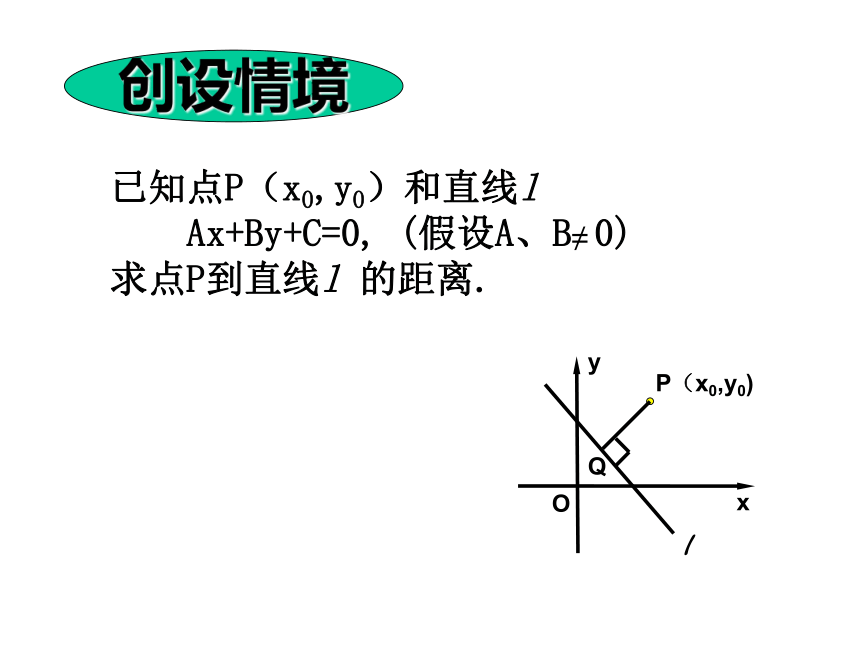
已知点P(x0,y0)和直线l
Ax+By+C=0, (假设A、B≠ 0)
求点P到直线l 的距离.
x
y
O
l
P(x0,y0)
Q
创设情境
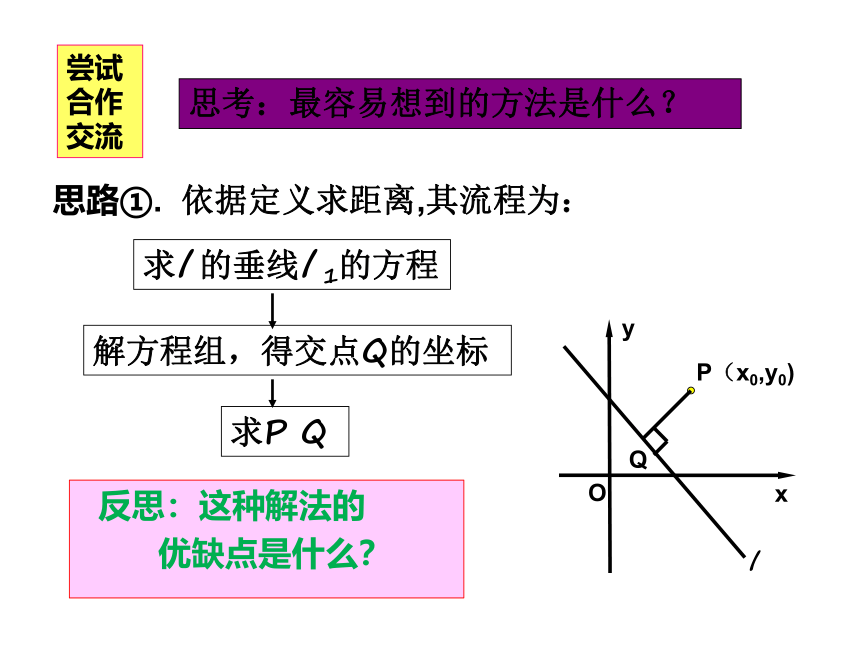
反思:这种解法的
优缺点是什么?
x
y
O
l
P(x0,y0)
Q
思考:最容易想到的方法是什么?
思路①. 依据定义求距离,其流程为:
求l 的垂线l 1的方程
解方程组,得交点Q的坐标
求P Q
尝试 合作 交流
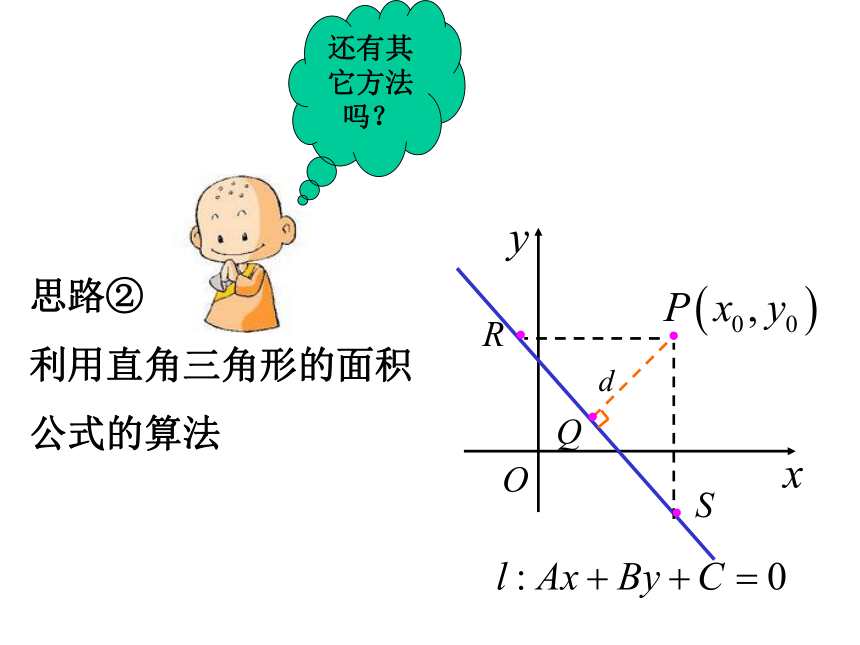
思路②
利用直角三角形的面积
公式的算法
·
·
·
·
还有其它方法吗?
过 程 设 计:
过点 作 轴、 轴的垂线 交于点
求出
利用勾股定理求出
根据面积相等知 得到点 到 的距离
用 表示点 的坐标
方法②
利用直角三角形面积公式的算法框图
思路② :P(x0,y0), l:Ax+By+C=0, 设AB≠0,
O
y
x
l
d
Q
P
R
S
O
y
x
l
d
Q
P
R
S
由三角形面积公式可得:
反思2:
反思1:在使用该公式前,须将直线方程化为一般式.
辨析反思
前面我们是在A,B均不为零的假设下推导出公式的, 若A,B中有一个为零,公式是否仍然成立?
公式的完善
1.当A=0,即L⊥y轴时
P
Q
x
y
o
L
2
0
0
2
|
|
|
|
B
A
C
By
Ax
PQ
+
+
+
=
2.当B=0,即L⊥x轴时
P
Q
x
y
o
L
3.当P点在L上时,
公式成立
公式明显成立
公式成立
公式结构特点
(1)分子是P点坐标( , )代入直线方程;
(2)分母是直线未知数x、y系数平方和的算术根
例1:求点P(-1,2)到直线①2x+y-10=0; ②3x=2的距离。
解: ①根据点到直线的距离公式,得
②如图,直线3x=2平行于y轴,
O
y
x
l:3x=2
P(-1,2)
用公式验证,结果怎样?
求下列点到相应直线的距离d:
(1) P(0,0) l: 3x-2y+4=0
(2) P(-1,2) l: x- y =-
(3) P(3,-5) l: x = -1
课堂练习
直线的方程应化为一般式!
点A(a,6)到直线3x-4y=2的距
离等于4,求a的值.
应用理解
a=2 或
练习反馈题
(1)P(—2,3)到直线y= —2的距离是________
(2)P(—1,1)到直线3x= 2的距离是_________
(3)P(2,—3)到直线x+2y+4= 0的距离是_______
(4)P(—1,1)到直线2x+y—10= 0的距离是______
(5)P(2,0)到直线y= 2x的距离是______
5
0
任意两条平行直线都可以写成如下形式:
l1 :Ax+By+C1=0
l2 :Ax+By+C2=0
O
y
x
l2
l1
P
Q
思考:任意两条平行线的距离是多少呢?
注:用两平行线间距离公式须将方程中x、y的系数化为
对应相同的形式。
(两平行线间
的距离公式)
点 到 直 线 的 距 离
1.此公式的作用是求点到直线的距离;
2.此公式是在A、B≠0的前提下推导的;
3.如果A=0或B=0,此公式恰好也成立;
4.如果A=0或B=0,一般不用此公式;
5.用此公式时直线要先化成一般式。
小结
反馈练习:
( )
( )
D
B
( )
( )
D
A
P在x轴上,P到直线l1: x - y +7=0与直线l2: 12x-5y+40=0的距离相等,求P点坐标。
解:设P(x,0),
根据P到l1、 l2距离相等,列式为
解得:
所以P点坐标为:
⑴
5.完成下列解题过程:
=
用解析法证明:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。
⑵
证明:建立如图直角坐标系,设P (x,0),x∈( )
O
A(a,0)
C(-a,0)
B(0,b)
x
y
E
F
P
可求得lAB:( )
lCB:( )
|PE|=( )
|PF|=( )
A到BC的距离h=( )
因为|PE|+|PF|=h,所以原命题得证。
尝试回忆
1.点 到 直 线 的 距 离:
2.两平行线间的距离公式:
要记牢哦!很重要的!
仓库
铁路
仓库
l
.
P
点到直线的距离
l
l
P
.
o
x
y
: Ax+By+C=0
(x0,y0)
点到直线的距离
点到直线的距离
x
y
O
l
P(x0,y0)
Q
点到直线的距离的定义
点到直线的距离公式的推导过程
过点 作直线 的垂线,垂足为 点,线段 的长度叫做点 到直线 的距离.
已知点P(x0,y0)和直线l
Ax+By+C=0, (假设A、B≠ 0)
求点P到直线l 的距离.
x
y
O
l
P(x0,y0)
Q
创设情境
反思:这种解法的
优缺点是什么?
x
y
O
l
P(x0,y0)
Q
思考:最容易想到的方法是什么?
思路①. 依据定义求距离,其流程为:
求l 的垂线l 1的方程
解方程组,得交点Q的坐标
求P Q
尝试 合作 交流
思路②
利用直角三角形的面积
公式的算法
·
·
·
·
还有其它方法吗?
过 程 设 计:
过点 作 轴、 轴的垂线 交于点
求出
利用勾股定理求出
根据面积相等知 得到点 到 的距离
用 表示点 的坐标
方法②
利用直角三角形面积公式的算法框图
思路② :P(x0,y0), l:Ax+By+C=0, 设AB≠0,
O
y
x
l
d
Q
P
R
S
O
y
x
l
d
Q
P
R
S
由三角形面积公式可得:
反思2:
反思1:在使用该公式前,须将直线方程化为一般式.
辨析反思
前面我们是在A,B均不为零的假设下推导出公式的, 若A,B中有一个为零,公式是否仍然成立?
公式的完善
1.当A=0,即L⊥y轴时
P
Q
x
y
o
L
2
0
0
2
|
|
|
|
B
A
C
By
Ax
PQ
+
+
+
=
2.当B=0,即L⊥x轴时
P
Q
x
y
o
L
3.当P点在L上时,
公式成立
公式明显成立
公式成立
公式结构特点
(1)分子是P点坐标( , )代入直线方程;
(2)分母是直线未知数x、y系数平方和的算术根
例1:求点P(-1,2)到直线①2x+y-10=0; ②3x=2的距离。
解: ①根据点到直线的距离公式,得
②如图,直线3x=2平行于y轴,
O
y
x
l:3x=2
P(-1,2)
用公式验证,结果怎样?
求下列点到相应直线的距离d:
(1) P(0,0) l: 3x-2y+4=0
(2) P(-1,2) l: x- y =-
(3) P(3,-5) l: x = -1
课堂练习
直线的方程应化为一般式!
点A(a,6)到直线3x-4y=2的距
离等于4,求a的值.
应用理解
a=2 或
练习反馈题
(1)P(—2,3)到直线y= —2的距离是________
(2)P(—1,1)到直线3x= 2的距离是_________
(3)P(2,—3)到直线x+2y+4= 0的距离是_______
(4)P(—1,1)到直线2x+y—10= 0的距离是______
(5)P(2,0)到直线y= 2x的距离是______
5
0
任意两条平行直线都可以写成如下形式:
l1 :Ax+By+C1=0
l2 :Ax+By+C2=0
O
y
x
l2
l1
P
Q
思考:任意两条平行线的距离是多少呢?
注:用两平行线间距离公式须将方程中x、y的系数化为
对应相同的形式。
(两平行线间
的距离公式)
点 到 直 线 的 距 离
1.此公式的作用是求点到直线的距离;
2.此公式是在A、B≠0的前提下推导的;
3.如果A=0或B=0,此公式恰好也成立;
4.如果A=0或B=0,一般不用此公式;
5.用此公式时直线要先化成一般式。
小结
反馈练习:
( )
( )
D
B
( )
( )
D
A
P在x轴上,P到直线l1: x - y +7=0与直线l2: 12x-5y+40=0的距离相等,求P点坐标。
解:设P(x,0),
根据P到l1、 l2距离相等,列式为
解得:
所以P点坐标为:
⑴
5.完成下列解题过程:
=
用解析法证明:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。
⑵
证明:建立如图直角坐标系,设P (x,0),x∈( )
O
A(a,0)
C(-a,0)
B(0,b)
x
y
E
F
P
可求得lAB:( )
lCB:( )
|PE|=( )
|PF|=( )
A到BC的距离h=( )
因为|PE|+|PF|=h,所以原命题得证。
尝试回忆
1.点 到 直 线 的 距 离:
2.两平行线间的距离公式:
要记牢哦!很重要的!
