沪教版(上海)数学高二下册-12.1曲线和方程(2)(课件)(共15张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二下册-12.1曲线和方程(2)(课件)(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 379.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:19:49 | ||
图片预览






文档简介
(共15张PPT)
借助于平面直角坐标系用代数得方法研究平面上图形性质的学科称为平面解析几何
二元一次方程组有一解,无解,有无穷多解
两条直线相交,平行,重合
曲线和方程
若二元方程ax+by+c=0(a,b不全为0)与直线l满足以下两个关系:
(1)直线l上的点的坐标都是方程ax+by+c=0(a,b不全为0)的解;
(即:直线l上的点都满足方程ax+by+c=0(a,b不全为0) )
(2)以方程ax+by+c=0(a,b不全为0)的解为坐标的点都在直线l上.
l
那么这个方程ax+by+c=0(a,b不全为0)就叫做这条直线l的方程;
这条直线l就叫做这个方程ax+by+c=0(a,b不全为0)的直线.
:ax+by+c=0
回顾:直线与方程
y
x
0
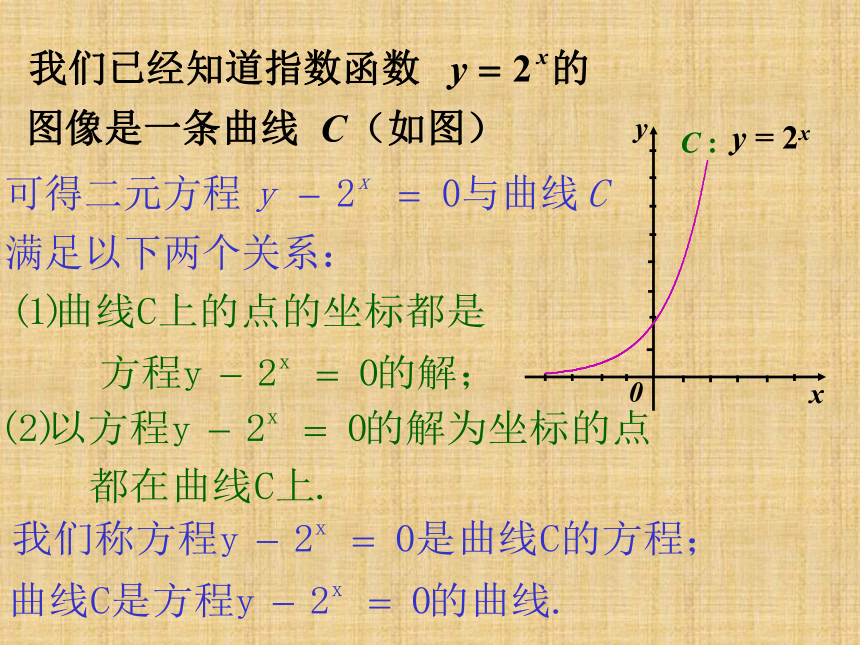
y = 2x
在描述曲线所满足的某种性质时,我们也可用方程来表示文字叙述,如:
圆的描述:
代数表示:
语言叙述:
到某一定点的距离等于定值
整理得:
(1)以方程(1)的任意一组解(x,y)为坐标的点都满足“到定点A的距离为r”
(2)反之,满足“到定点A的距离为r”的点的坐标都满足方程(1)
圆A上的点
方程(1)的解
1-1对应
直角坐标系中,如果某曲线C上的点与一个方程F(x,y)=0的实数解建立了如下的关系:
①曲线C上的点的坐标,都是方程F(x,y)=0的解;
②以方程F(x,y)=0的解为坐标的点,都是曲线C上的点。
那么,方程F(x,y)=0叫做曲线C的方程,曲线C叫做方程F(x,y)=0的曲线。
曲线的方程与方程的曲线定义
注:(1)两个条件缺一不可;
前提:
条件:
条件:
结论:
(2)两个结论同时成立.
用集合的关系来理解:
练习:
如果曲线C上任意一点的坐标都是方程F(x,y)=0
的解,那么下列命题正确的是( )
(A)曲线C的方程是F(x,y)=0;
(B)曲线C上的点都在方程F(x,y)=0的曲线上;
(C)方程F(x,y)=0的曲线是C;
(D)以方程F(x,y)=0的解为坐标的点
都在曲线C上.
B
下述方程分别表示图1曲线吗?为什么?
① - =0
|x|-|y|=0
②
③
x-|y|=0
图1
O
Y
1
1
X
O
Y
1
1
X
-1
-1
B
1
1
O
X
Y
-1
C
运用反例,揭示内涵
X
O
Y
1
1
A
例1 证明以坐标原点为圆心,半径等于5的圆O的方程是x2 +y2 = 25,并判断点A(3,-4),B(-3,2)是否在这个圆上.
证明:(1)设M1(x1,y1)是圆O上任意一点.那么点M1到坐标原
点的距离等于5,所以 得x12 +y12 = 25.
即 (x1,y1) 是方程x2 +y2 = 25的解.
(2)设 (x2 ,y2) 是方程x2 +y2 = 25的任意一个解,
那么x22 +y22 = 25,两边开方,得
即点M2 (x2,y2)到坐标原点的距离等于5,点M 2(x2,y2)是这个圆上的一点.
根据曲线方程的定义,由(1)、(2)可知, x2 +y2 = 25是以坐标原点为圆心,半径等于5的圆的方程.
(满足条件1)
(满足条件2)
第一步,设M1 (x1,y1)是曲线C上任一点,证明(x1,y1)是f(x,y)=0的解;
归纳:
(一) 证明已知曲线的方程的方法和步骤
第二步,设(x2,y2)是F(x,y)=0的任意一个解,证明点M2 (x2,y2)在曲线C上.
(二)要判断点是否在曲线上,只要看其坐标是否满足曲线的方程即可。
如果曲线C的方程是f(x,y)=0,那么点P(x0,y0)在曲线C上的充要条件是f(x0,y0)=0
例2 求证:到两坐标轴距离相等的点的轨迹C的方程不是x-y=0.
(不满足条件1)
直角坐标系中,如果某曲线C上的点与一个二元方程F(x,y)=0的实数解建立了如下的关系:
①曲线C上的点的坐标,都是方程F(x,y)=0的解;
②以方程F(x,y)=0的解为坐标的点,都是曲线C上的点。
那么,方程F(x,y)=0叫做曲线C的方程,曲线C叫做方程F(x,y)=0的曲线。
注:(1)两个条件缺一不可;
前提:
条件:
条件:
结论:
(2)两个结论同时成立。
小结
曲线的方程与方程的曲线定义
借助于平面直角坐标系用代数得方法研究平面上图形性质的学科称为平面解析几何
二元一次方程组有一解,无解,有无穷多解
两条直线相交,平行,重合
曲线和方程
若二元方程ax+by+c=0(a,b不全为0)与直线l满足以下两个关系:
(1)直线l上的点的坐标都是方程ax+by+c=0(a,b不全为0)的解;
(即:直线l上的点都满足方程ax+by+c=0(a,b不全为0) )
(2)以方程ax+by+c=0(a,b不全为0)的解为坐标的点都在直线l上.
l
那么这个方程ax+by+c=0(a,b不全为0)就叫做这条直线l的方程;
这条直线l就叫做这个方程ax+by+c=0(a,b不全为0)的直线.
:ax+by+c=0
回顾:直线与方程
y
x
0
y = 2x
在描述曲线所满足的某种性质时,我们也可用方程来表示文字叙述,如:
圆的描述:
代数表示:
语言叙述:
到某一定点的距离等于定值
整理得:
(1)以方程(1)的任意一组解(x,y)为坐标的点都满足“到定点A的距离为r”
(2)反之,满足“到定点A的距离为r”的点的坐标都满足方程(1)
圆A上的点
方程(1)的解
1-1对应
直角坐标系中,如果某曲线C上的点与一个方程F(x,y)=0的实数解建立了如下的关系:
①曲线C上的点的坐标,都是方程F(x,y)=0的解;
②以方程F(x,y)=0的解为坐标的点,都是曲线C上的点。
那么,方程F(x,y)=0叫做曲线C的方程,曲线C叫做方程F(x,y)=0的曲线。
曲线的方程与方程的曲线定义
注:(1)两个条件缺一不可;
前提:
条件:
条件:
结论:
(2)两个结论同时成立.
用集合的关系来理解:
练习:
如果曲线C上任意一点的坐标都是方程F(x,y)=0
的解,那么下列命题正确的是( )
(A)曲线C的方程是F(x,y)=0;
(B)曲线C上的点都在方程F(x,y)=0的曲线上;
(C)方程F(x,y)=0的曲线是C;
(D)以方程F(x,y)=0的解为坐标的点
都在曲线C上.
B
下述方程分别表示图1曲线吗?为什么?
① - =0
|x|-|y|=0
②
③
x-|y|=0
图1
O
Y
1
1
X
O
Y
1
1
X
-1
-1
B
1
1
O
X
Y
-1
C
运用反例,揭示内涵
X
O
Y
1
1
A
例1 证明以坐标原点为圆心,半径等于5的圆O的方程是x2 +y2 = 25,并判断点A(3,-4),B(-3,2)是否在这个圆上.
证明:(1)设M1(x1,y1)是圆O上任意一点.那么点M1到坐标原
点的距离等于5,所以 得x12 +y12 = 25.
即 (x1,y1) 是方程x2 +y2 = 25的解.
(2)设 (x2 ,y2) 是方程x2 +y2 = 25的任意一个解,
那么x22 +y22 = 25,两边开方,得
即点M2 (x2,y2)到坐标原点的距离等于5,点M 2(x2,y2)是这个圆上的一点.
根据曲线方程的定义,由(1)、(2)可知, x2 +y2 = 25是以坐标原点为圆心,半径等于5的圆的方程.
(满足条件1)
(满足条件2)
第一步,设M1 (x1,y1)是曲线C上任一点,证明(x1,y1)是f(x,y)=0的解;
归纳:
(一) 证明已知曲线的方程的方法和步骤
第二步,设(x2,y2)是F(x,y)=0的任意一个解,证明点M2 (x2,y2)在曲线C上.
(二)要判断点是否在曲线上,只要看其坐标是否满足曲线的方程即可。
如果曲线C的方程是f(x,y)=0,那么点P(x0,y0)在曲线C上的充要条件是f(x0,y0)=0
例2 求证:到两坐标轴距离相等的点的轨迹C的方程不是x-y=0.
(不满足条件1)
直角坐标系中,如果某曲线C上的点与一个二元方程F(x,y)=0的实数解建立了如下的关系:
①曲线C上的点的坐标,都是方程F(x,y)=0的解;
②以方程F(x,y)=0的解为坐标的点,都是曲线C上的点。
那么,方程F(x,y)=0叫做曲线C的方程,曲线C叫做方程F(x,y)=0的曲线。
注:(1)两个条件缺一不可;
前提:
条件:
条件:
结论:
(2)两个结论同时成立。
小结
曲线的方程与方程的曲线定义
