沪教版(上海)数学高二下册-12.3椭圆的标准方程_(1)(课件)(共17张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二下册-12.3椭圆的标准方程_(1)(课件)(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 21:39:54 | ||
图片预览




文档简介
(共17张PPT)
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
一.问题情境
注意:
椭圆定义中容易遗漏的三处地方:
(1) 必须在平面内.
(2)两个定点---两点间距离确定.
(3)绳长--轨迹上任意点到两定点距离和确定.
思考:在同样的绳长下,两定点间距离较长,则所画出的
椭圆较扁( 线段)在同样的绳长下,两定点间距离较短,则所画出的椭圆较圆( 圆)
由此可知,椭圆的形状与两定点间距离、绳长有关.
1 椭圆定义:
平面内与两个定点 的距离和等于常数(大于
)的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .
二、复习回顾:
PF1+PF2=2a (2a>2c>0, F1F2=2c)
y
x
O
r
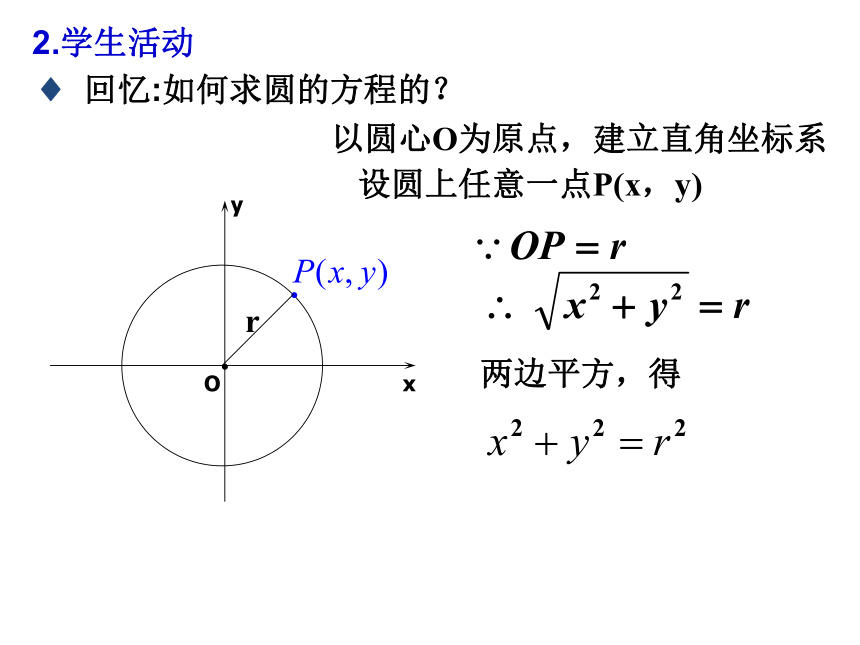
设圆上任意一点P(x,y)
以圆心O为原点,建立直角坐标系
两边平方,得
2.学生活动
回忆:如何求圆的方程的?
2.学生活动:
求动点轨迹方程的一般步骤:
(1)建立适当的坐标系,用有序实数对表示曲线
上任意一点M的坐标;
(2)写出适合条件P的点M的集合;(可以省略,
直接列出曲线方程)
(3)用坐标表示条件P(M),列出方程
(5)证明以化简后的方程的解为坐标的点都是
曲线上的点(可以省略不写,如有特殊情况,可以
适当予以说明)
(4)化方程 为最简形式;
3.代坐标
4.化简方程
坐标法
5.验证
1.建系设点
2.关系式
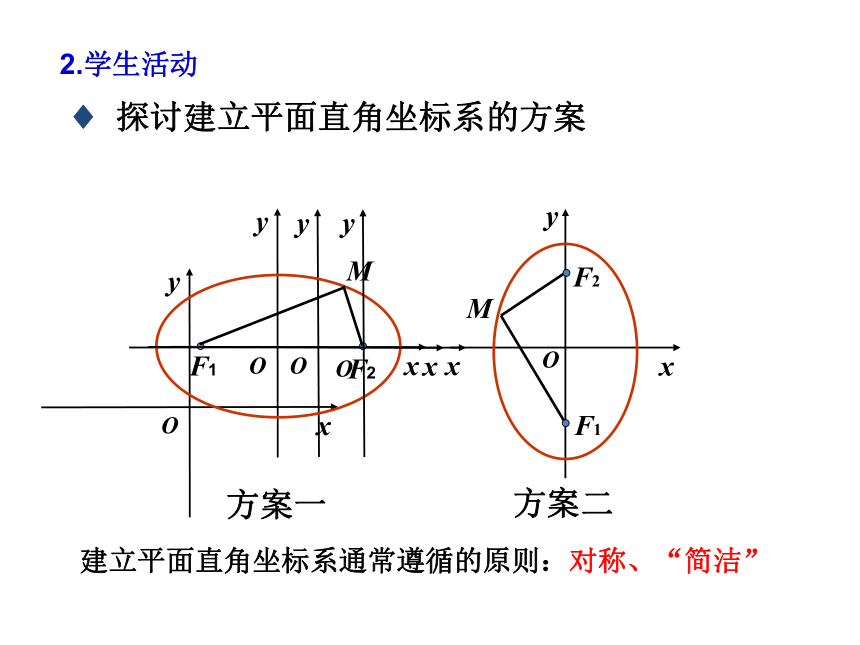
2.学生活动
探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:对称、“简洁”
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
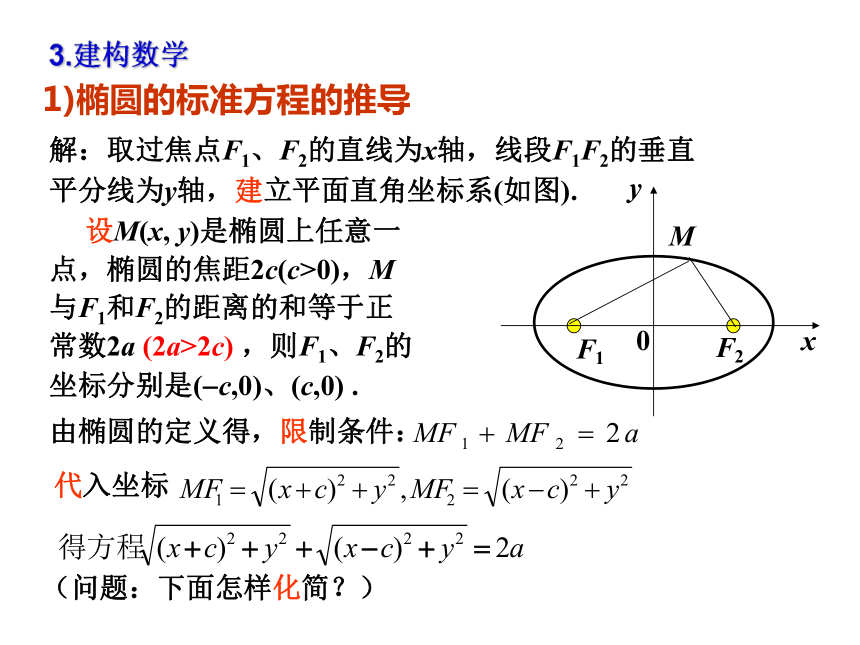
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是( c,0)、(c,0) .
x
F1
F2
M
0
y
3.建构数学
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标
1)椭圆的标准方程的推导
两边除以 得
由椭圆定义可知
整理得
两边再平方,得
移项,再平方
总体印象:对称、简洁,“像”直线方程的截距式
焦点在y轴:
焦点在x轴:
2)椭圆的标准方程
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
MF1+MF2=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
3)两类标准方程的对照表
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
练习 : 已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.
解:
以两焦点F1、F2所在直线为x轴,线段F1F2的垂直平分线为
y 轴,建立如图所示的直角坐标系xOy,则这个椭圆的标准
方程可设为
根据题意有
即
因此,这个椭圆的标准方程为
x
y
O
F1
F2
4.数学应用
练习:
1、 已知椭圆的方程为: ,请填空:
(1) a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且CF1=2,则CF2=___.
变题: 若椭圆的方程为 ,试口答完成(1).
若方程 表示焦点在y轴上的椭圆,
求k的取值范围;
探究:
若方程表示椭圆呢
5
4
3
6
(-3,0)、(3,0)
8
课堂练习:
1.口答:下列方程哪些表示椭圆?
解:
例1 :将圆 = 4上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,
并说明它是什么曲线?
y
x
o
设所的曲线上任一点的坐标为(x,y),圆 =4上的对应点的坐标为(x’,y’),由题意可得:
因为 =4
所以
即
1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆。
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法;
例2、写出适合下列条件的椭圆的标准方程
(1) a =4,b=1,焦点在 x 轴上;
(2) a =4,b=1,焦点在坐标轴上;
(3) 两个焦点的坐标是( 0 ,-2)和( 0 ,2),并且经
过点P( -1.5 ,2.5).
解: 因为椭圆的焦点在y轴上,
设它的标准方程为
∵ c=2,且 c2= a2 - b2
∴ 4= a2 - b2 ……①
又∵椭圆经过点
∴ ……②
联立①②可求得:
∴椭圆的标准方程为
(法一)
x
y
F1
F2
P
或
(法二) 因为椭圆的焦点在y轴上,所以设它的
标准方程为
由椭圆的定义知,
所以所求椭圆的标准方程为
5、回顾小结
求椭圆标准方程的方法
一种方法:
二类方程:
三个意识:
求美意识, 求简意识,前瞻意识
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
一.问题情境
注意:
椭圆定义中容易遗漏的三处地方:
(1) 必须在平面内.
(2)两个定点---两点间距离确定.
(3)绳长--轨迹上任意点到两定点距离和确定.
思考:在同样的绳长下,两定点间距离较长,则所画出的
椭圆较扁( 线段)在同样的绳长下,两定点间距离较短,则所画出的椭圆较圆( 圆)
由此可知,椭圆的形状与两定点间距离、绳长有关.
1 椭圆定义:
平面内与两个定点 的距离和等于常数(大于
)的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .
二、复习回顾:
PF1+PF2=2a (2a>2c>0, F1F2=2c)
y
x
O
r
设圆上任意一点P(x,y)
以圆心O为原点,建立直角坐标系
两边平方,得
2.学生活动
回忆:如何求圆的方程的?
2.学生活动:
求动点轨迹方程的一般步骤:
(1)建立适当的坐标系,用有序实数对表示曲线
上任意一点M的坐标;
(2)写出适合条件P的点M的集合;(可以省略,
直接列出曲线方程)
(3)用坐标表示条件P(M),列出方程
(5)证明以化简后的方程的解为坐标的点都是
曲线上的点(可以省略不写,如有特殊情况,可以
适当予以说明)
(4)化方程 为最简形式;
3.代坐标
4.化简方程
坐标法
5.验证
1.建系设点
2.关系式
2.学生活动
探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:对称、“简洁”
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是( c,0)、(c,0) .
x
F1
F2
M
0
y
3.建构数学
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标
1)椭圆的标准方程的推导
两边除以 得
由椭圆定义可知
整理得
两边再平方,得
移项,再平方
总体印象:对称、简洁,“像”直线方程的截距式
焦点在y轴:
焦点在x轴:
2)椭圆的标准方程
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
MF1+MF2=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
3)两类标准方程的对照表
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
练习 : 已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.
解:
以两焦点F1、F2所在直线为x轴,线段F1F2的垂直平分线为
y 轴,建立如图所示的直角坐标系xOy,则这个椭圆的标准
方程可设为
根据题意有
即
因此,这个椭圆的标准方程为
x
y
O
F1
F2
4.数学应用
练习:
1、 已知椭圆的方程为: ,请填空:
(1) a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且CF1=2,则CF2=___.
变题: 若椭圆的方程为 ,试口答完成(1).
若方程 表示焦点在y轴上的椭圆,
求k的取值范围;
探究:
若方程表示椭圆呢
5
4
3
6
(-3,0)、(3,0)
8
课堂练习:
1.口答:下列方程哪些表示椭圆?
解:
例1 :将圆 = 4上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,
并说明它是什么曲线?
y
x
o
设所的曲线上任一点的坐标为(x,y),圆 =4上的对应点的坐标为(x’,y’),由题意可得:
因为 =4
所以
即
1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆。
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法;
例2、写出适合下列条件的椭圆的标准方程
(1) a =4,b=1,焦点在 x 轴上;
(2) a =4,b=1,焦点在坐标轴上;
(3) 两个焦点的坐标是( 0 ,-2)和( 0 ,2),并且经
过点P( -1.5 ,2.5).
解: 因为椭圆的焦点在y轴上,
设它的标准方程为
∵ c=2,且 c2= a2 - b2
∴ 4= a2 - b2 ……①
又∵椭圆经过点
∴ ……②
联立①②可求得:
∴椭圆的标准方程为
(法一)
x
y
F1
F2
P
或
(法二) 因为椭圆的焦点在y轴上,所以设它的
标准方程为
由椭圆的定义知,
所以所求椭圆的标准方程为
5、回顾小结
求椭圆标准方程的方法
一种方法:
二类方程:
三个意识:
求美意识, 求简意识,前瞻意识
