沪教版(上海)数学高二下册-12.5双曲线的标准方程_(1)(课件)(共16张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二下册-12.5双曲线的标准方程_(1)(课件)(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 525.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
一
复习引入
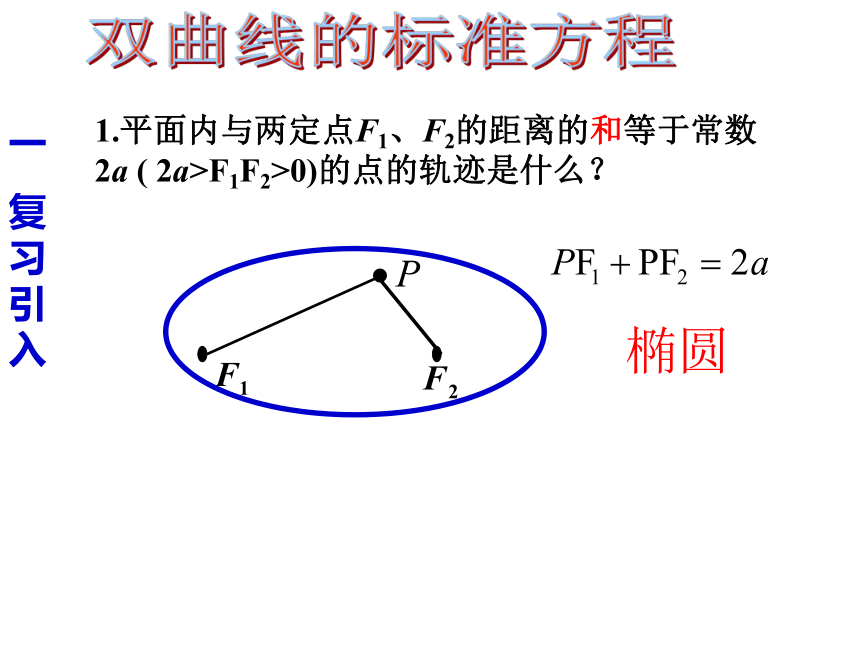
1.平面内与两定点F1、F2的距离的和等于常数2a ( 2a>F1F2>0)的点的轨迹是什么?
椭圆
(1) PF1-PF2=2a
一
复习引入
2.平面内与两定点F1、F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹是什么?
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹叫做双曲线。
o
F2
F1
P
| PF1-PF2 | = 2a
(差的绝对值)
① 两个定点F1、F2——双曲线的焦点;
② F1F2=2c ——焦距。
(双曲线的右支)
(双曲线的左支)
(2) PF2-PF1=2a
(双曲线)
二
释疑精讲
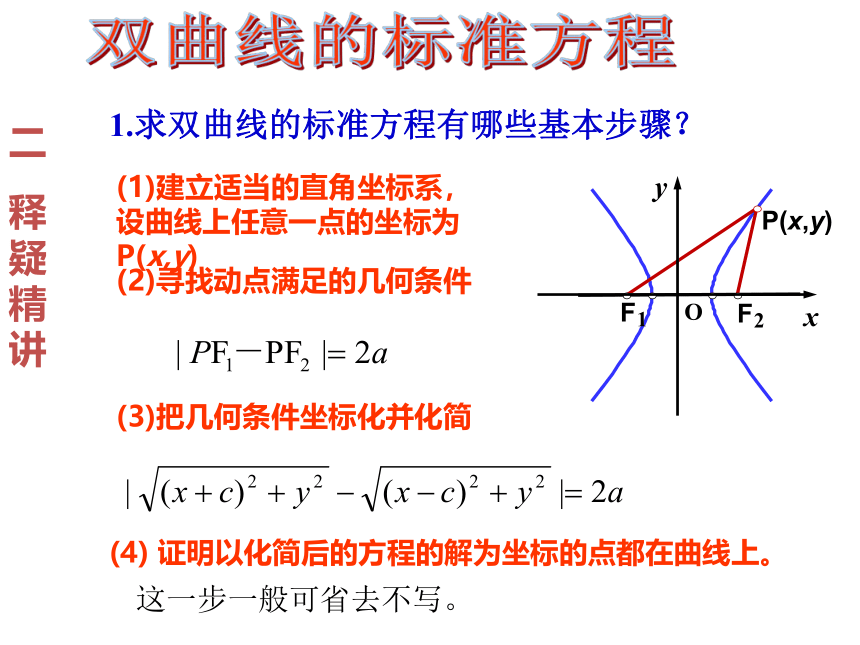
(1)建立适当的直角坐标系,设曲线上任意一点的坐标为P(x,y)
(2)寻找动点满足的几何条件
(3)把几何条件坐标化并化简
F
2
F
1
P(x,y)
x
O
y
(4) 证明以化简后的方程的解为坐标的点都在曲线上。
1.求双曲线的标准方程有哪些基本步骤?
二
释疑精讲
F
2
F
1
P
x
O
y
O
P
F2
F1
x
y
二
释疑精讲
3.焦点在x轴和焦点在y轴的双曲线的标准方程有何区别?
焦点在x轴上, x2项的系数为正;
焦点在y轴上, y2项的系数为正。
二
释疑精讲
4. 你能归纳出求椭圆的标准方程的基本类型吗?
把双曲线方程化成标准形式后,
x2项的系数为正,焦点在x轴上;
y2项的系数为正,焦点在y轴上。
三
基本练习
1.写出下列椭圆或双曲线的焦点坐标,并归纳出确定焦点位置的方法:
F1(5,0),
F2(-5,0)
F1(0,5),
F2(0,-5)
F1(4,0),
F2(-4,0)
F1(0,4),
F2(0,-4)
把椭圆方程化成标准形式后,
x2项的分母较大,焦点在x轴上;
y2项的分母较大,焦点在y轴上。
三
基本练习
2.写出适合下列条件的双曲线的标准方程:
三
基本练习
2.写出适合下列条件的双曲线的标准方程:
解:
根据双曲线的焦点在 x 轴上,设它的标准方程为:
由题知点P的轨迹是双曲线的右支,
∵ 2a = 6, c=5
∴ a = 3, c = 5
∴ b2 = 52-32 =16
所以点P的轨迹方程为:
(x>0)
1. 已知两定点F1(-5,0),F2(5,0),平面上一动点P,PF1-PF2= 6,求点P的轨迹方程。
四
变式练习
四
变式练习
B
五
归纳小结
定义
图象
方程
焦点
a.b.c 的关系
| MF1-MF2 | =2a(0 < 2a( ±c, 0) (0, ± c)
定 义
方 程
焦 点
a.b.c的关系
(±c,0)
(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
双曲线与椭圆之间的区别与联系
|MF1-MF2|=2a
MF1+MF2=2a
椭 圆
双曲线
(0,±c)
(0,±c)
五
归纳小结
六
拓展深化
o
F2
F1
M
我们知道,平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹叫做双曲线。
试分别讨论当常数等于F1F2和大于F1F2时点的轨迹。
六
拓展深化
o
F2
F1
M
我们知道,平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹叫做双曲线。
试分别讨论当常数等于F1F2和大于F1F2时点的轨迹。
当2a = 2c时,点M的轨迹是两条射线;
当2a> 2c时,点M的轨迹不存在。
F1
F2
M
一
复习引入
1.平面内与两定点F1、F2的距离的和等于常数2a ( 2a>F1F2>0)的点的轨迹是什么?
椭圆
(1) PF1-PF2=2a
一
复习引入
2.平面内与两定点F1、F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹是什么?
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹叫做双曲线。
o
F2
F1
P
| PF1-PF2 | = 2a
(差的绝对值)
① 两个定点F1、F2——双曲线的焦点;
② F1F2=2c ——焦距。
(双曲线的右支)
(双曲线的左支)
(2) PF2-PF1=2a
(双曲线)
二
释疑精讲
(1)建立适当的直角坐标系,设曲线上任意一点的坐标为P(x,y)
(2)寻找动点满足的几何条件
(3)把几何条件坐标化并化简
F
2
F
1
P(x,y)
x
O
y
(4) 证明以化简后的方程的解为坐标的点都在曲线上。
1.求双曲线的标准方程有哪些基本步骤?
二
释疑精讲
F
2
F
1
P
x
O
y
O
P
F2
F1
x
y
二
释疑精讲
3.焦点在x轴和焦点在y轴的双曲线的标准方程有何区别?
焦点在x轴上, x2项的系数为正;
焦点在y轴上, y2项的系数为正。
二
释疑精讲
4. 你能归纳出求椭圆的标准方程的基本类型吗?
把双曲线方程化成标准形式后,
x2项的系数为正,焦点在x轴上;
y2项的系数为正,焦点在y轴上。
三
基本练习
1.写出下列椭圆或双曲线的焦点坐标,并归纳出确定焦点位置的方法:
F1(5,0),
F2(-5,0)
F1(0,5),
F2(0,-5)
F1(4,0),
F2(-4,0)
F1(0,4),
F2(0,-4)
把椭圆方程化成标准形式后,
x2项的分母较大,焦点在x轴上;
y2项的分母较大,焦点在y轴上。
三
基本练习
2.写出适合下列条件的双曲线的标准方程:
三
基本练习
2.写出适合下列条件的双曲线的标准方程:
解:
根据双曲线的焦点在 x 轴上,设它的标准方程为:
由题知点P的轨迹是双曲线的右支,
∵ 2a = 6, c=5
∴ a = 3, c = 5
∴ b2 = 52-32 =16
所以点P的轨迹方程为:
(x>0)
1. 已知两定点F1(-5,0),F2(5,0),平面上一动点P,PF1-PF2= 6,求点P的轨迹方程。
四
变式练习
四
变式练习
B
五
归纳小结
定义
图象
方程
焦点
a.b.c 的关系
| MF1-MF2 | =2a(0 < 2a
定 义
方 程
焦 点
a.b.c的关系
(±c,0)
(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
双曲线与椭圆之间的区别与联系
|MF1-MF2|=2a
MF1+MF2=2a
椭 圆
双曲线
(0,±c)
(0,±c)
五
归纳小结
六
拓展深化
o
F2
F1
M
我们知道,平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹叫做双曲线。
试分别讨论当常数等于F1F2和大于F1F2时点的轨迹。
六
拓展深化
o
F2
F1
M
我们知道,平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹叫做双曲线。
试分别讨论当常数等于F1F2和大于F1F2时点的轨迹。
当2a = 2c时,点M的轨迹是两条射线;
当2a> 2c时,点M的轨迹不存在。
F1
F2
M
