沪教版(上海)数学高二下册-13.1复数的概念(课件)(共24张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二下册-13.1复数的概念(课件)(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 312.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 21:42:25 | ||
图片预览







文档简介
(共24张PPT)
复 数
13.1复数的概念
知识与技能目标:了解引进复数的必要性, 理解数系的扩充过程;理解复数的基本概念、代数表示法;掌握复数相等的概念
过程与方法目标:经历数系扩充的过程,体会类比推理思想在数系扩充过程中的作用;体会复数分类中的分类讨论思想方法;掌握复数相等问题中的转化化归和方程的思想方法的运用.
情感、态度与价值观目标:在经历数系扩充的过程中,体验数学发现和创造的喜悦;;感受数学理性思维在数系扩充中的作用;养成勇于知疑问难、善于探索的学习习惯和思维品质.
学习目标
问题:在实数集中求解下面的方程
一、课题引入
能否把实数集扩充解决上面问题?
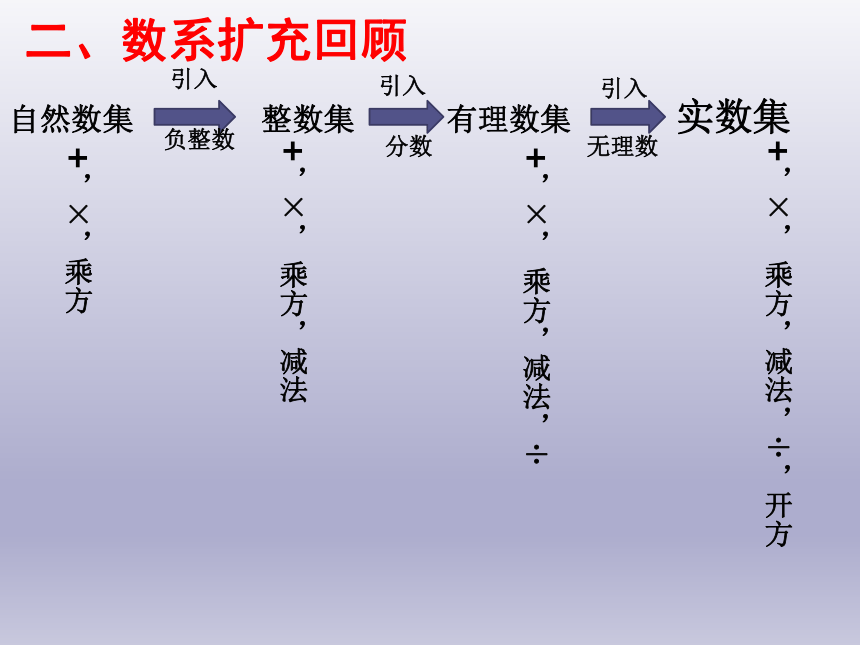
二、数系扩充回顾
探究问题一:数系扩充中,扩充几次,有什么共同特点?观察下面方程:
(1)在自然数集中方程x+4=0有解吗
(2)在整数集中方程x+4=0有解吗
(3)在整数集中方程3x-2=0有解吗
(4)在有理数集中方程3x-2=0有解吗
(5)在有理数集中方程x2-2=0有解吗
(6)在实数集中方程x2-2=0有解吗
自然数集 整数集 有理数集 实数集
二、数系扩充回顾
引入
分数
引入
引入
负整数
无理数
+,×,乘方
+,×, 乘方,减法
+,×, 乘方,减法,÷
+,×, 乘方,减法,÷,开方
①增添了新元素;
②原有的一些基本关系和运算法则在新数集里仍能运用;
③新数集解决了原数集一些不能解决的问题.
探究问题二:数系扩充中,有什么共同特点?
类比推理的数学思想
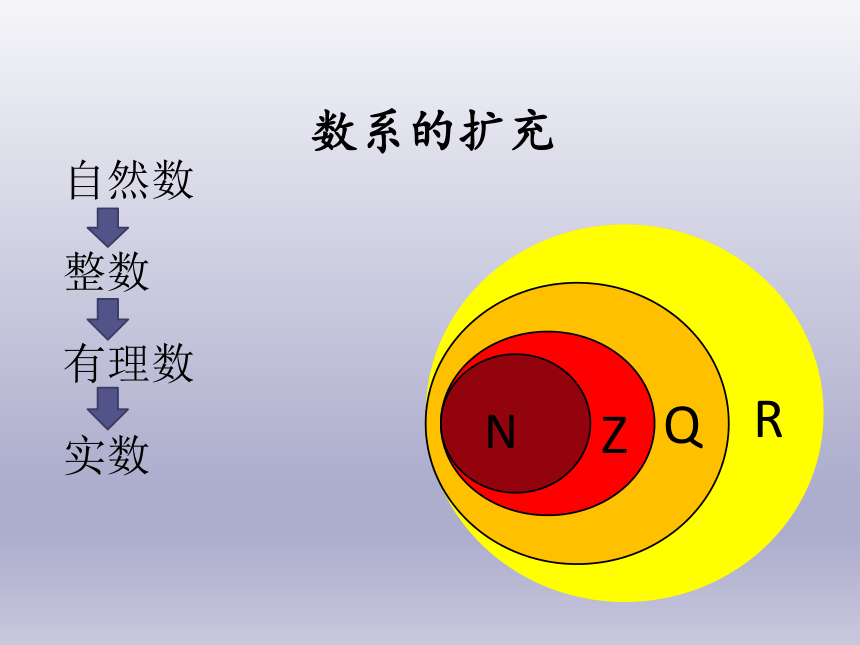
数系的扩充
自然数
整数
有理数
实数
R
Q
Z
N
继续解方程:
三、实数集扩充
有意义吗?
(1)
(2)实数集的扩充需要加入哪些元素?
探究问题三
1637年,法国数学家笛卡尔把这些数叫做“虚数”
(R.Descartes,1596~1661)
笛卡尔
如 等,当时很多数学家都认为这些数是没有意义的、虚无缥缈的
三、实数集扩充
1777年,瑞士数学家欧拉在其论文中首次使用符号“i ”(imaginary----想象的,假想的)
它满足: 称为虚数单位.
欧拉(L.Euler,1707 ~ 1783)
事实上,这些数最终都归结为-1的平方根
三、实数集扩充
三、实数集扩充
为扩充实数集,我们引入新数i,叫做虚数单位(imaginary unit),并规定:
(1)
(2)实数可以与i进行四则运算,在进行四则运算 时,原有的加法与乘法运算律仍然成立
(1)引入i 后能写出引题方程中要找的数吗?
(2)你能写出其他含有 i 的数吗?
(3)你能写出实数集扩充后的数集元素的一般形 式吗?
探究问题四:
类比求集合的并集
1、复数的概念:形如a+bi(a,b∈R)的数叫做复数, 通常用字母 z 表示.
四、复数概念
实部
虚部
2、复数的代数形式:z= a + bi
其中 称为虚数单位.
注意:复数实部和虚部都是实数
小练习
说出下列复数的实部和虚部:
3、复数的分类:
小练习
指出下列各数中,哪些为实数,哪些为虚数,哪些为纯虚数
4、复数集:全体复数所形成的集合叫做复数集,一般用字母 C 表示.
思考:复数集与实数集有什么关系?
总结:中学阶段数系扩充过程
实 数 集
有理数集
自然数集
整 数 集
复 数 集
添加虚数
例题赏析
例1、实数m取什么值时,复数
(1)实数 (2)虚数 (3)纯虚数
是:
解:(1)当m-1=0,即m=1时,复数z为实数。
(2)当m-1≠0,即m≠1时,复数z为虚数。
(3)当m+1=0,且m-1≠0时,即m=-1时,复数z为纯虚数。
分类讨论的思想
1、当 m 为何实数时,复数
(1)实数 (2)虚数 (3)纯虚数
(4) 0
是:
变式训练
探究问题四:如何定义两个复数相等?
反之,也成立.
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
,则
五、复数相等
转化化归和方程的思想,变未知为已知。
例2、已知
其中
,求
与 .
解:由已知得:
例题赏析(学生探究)
2、已知 其中x,y∈R,求x与y
解:根据复数相等的定义,得方程组
得
变式训练
1、(2015年高考)若集合A={i,i2,i3,i4}(i是虚数单位),B={1,-1},则A∩B等于( )
A.{-1} B.{1} C.{1,-1} D.
课堂练习:
C
2、若(2 -3x-2)+( -5x+6)i=0,求x得值.
x=2
3、求以2i-5的虚部为实部,以5i-2的实部为虚部的复数
2-2i
4、设x∈R,则“x=1”是“复数z=(x2-1)+(x+1)i为纯虚数”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
C
解析:由纯虚数的定义知:(x2-1)=0,且x+1≠0,则x=1.
六、课堂小结
(1)说说这节课的收获:你学到了什么?
(2)你还有什么疑惑?你进一步想探究的是什么?
八、作业设计
1、思考:复数集能否进一步扩充?
2、上网搜索复数的发展历史和在科学技术发展中的作用
3、教材P106,习题3.1 题3
谢谢!
复 数
13.1复数的概念
知识与技能目标:了解引进复数的必要性, 理解数系的扩充过程;理解复数的基本概念、代数表示法;掌握复数相等的概念
过程与方法目标:经历数系扩充的过程,体会类比推理思想在数系扩充过程中的作用;体会复数分类中的分类讨论思想方法;掌握复数相等问题中的转化化归和方程的思想方法的运用.
情感、态度与价值观目标:在经历数系扩充的过程中,体验数学发现和创造的喜悦;;感受数学理性思维在数系扩充中的作用;养成勇于知疑问难、善于探索的学习习惯和思维品质.
学习目标
问题:在实数集中求解下面的方程
一、课题引入
能否把实数集扩充解决上面问题?
二、数系扩充回顾
探究问题一:数系扩充中,扩充几次,有什么共同特点?观察下面方程:
(1)在自然数集中方程x+4=0有解吗
(2)在整数集中方程x+4=0有解吗
(3)在整数集中方程3x-2=0有解吗
(4)在有理数集中方程3x-2=0有解吗
(5)在有理数集中方程x2-2=0有解吗
(6)在实数集中方程x2-2=0有解吗
自然数集 整数集 有理数集 实数集
二、数系扩充回顾
引入
分数
引入
引入
负整数
无理数
+,×,乘方
+,×, 乘方,减法
+,×, 乘方,减法,÷
+,×, 乘方,减法,÷,开方
①增添了新元素;
②原有的一些基本关系和运算法则在新数集里仍能运用;
③新数集解决了原数集一些不能解决的问题.
探究问题二:数系扩充中,有什么共同特点?
类比推理的数学思想
数系的扩充
自然数
整数
有理数
实数
R
Q
Z
N
继续解方程:
三、实数集扩充
有意义吗?
(1)
(2)实数集的扩充需要加入哪些元素?
探究问题三
1637年,法国数学家笛卡尔把这些数叫做“虚数”
(R.Descartes,1596~1661)
笛卡尔
如 等,当时很多数学家都认为这些数是没有意义的、虚无缥缈的
三、实数集扩充
1777年,瑞士数学家欧拉在其论文中首次使用符号“i ”(imaginary----想象的,假想的)
它满足: 称为虚数单位.
欧拉(L.Euler,1707 ~ 1783)
事实上,这些数最终都归结为-1的平方根
三、实数集扩充
三、实数集扩充
为扩充实数集,我们引入新数i,叫做虚数单位(imaginary unit),并规定:
(1)
(2)实数可以与i进行四则运算,在进行四则运算 时,原有的加法与乘法运算律仍然成立
(1)引入i 后能写出引题方程中要找的数吗?
(2)你能写出其他含有 i 的数吗?
(3)你能写出实数集扩充后的数集元素的一般形 式吗?
探究问题四:
类比求集合的并集
1、复数的概念:形如a+bi(a,b∈R)的数叫做复数, 通常用字母 z 表示.
四、复数概念
实部
虚部
2、复数的代数形式:z= a + bi
其中 称为虚数单位.
注意:复数实部和虚部都是实数
小练习
说出下列复数的实部和虚部:
3、复数的分类:
小练习
指出下列各数中,哪些为实数,哪些为虚数,哪些为纯虚数
4、复数集:全体复数所形成的集合叫做复数集,一般用字母 C 表示.
思考:复数集与实数集有什么关系?
总结:中学阶段数系扩充过程
实 数 集
有理数集
自然数集
整 数 集
复 数 集
添加虚数
例题赏析
例1、实数m取什么值时,复数
(1)实数 (2)虚数 (3)纯虚数
是:
解:(1)当m-1=0,即m=1时,复数z为实数。
(2)当m-1≠0,即m≠1时,复数z为虚数。
(3)当m+1=0,且m-1≠0时,即m=-1时,复数z为纯虚数。
分类讨论的思想
1、当 m 为何实数时,复数
(1)实数 (2)虚数 (3)纯虚数
(4) 0
是:
变式训练
探究问题四:如何定义两个复数相等?
反之,也成立.
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
,则
五、复数相等
转化化归和方程的思想,变未知为已知。
例2、已知
其中
,求
与 .
解:由已知得:
例题赏析(学生探究)
2、已知 其中x,y∈R,求x与y
解:根据复数相等的定义,得方程组
得
变式训练
1、(2015年高考)若集合A={i,i2,i3,i4}(i是虚数单位),B={1,-1},则A∩B等于( )
A.{-1} B.{1} C.{1,-1} D.
课堂练习:
C
2、若(2 -3x-2)+( -5x+6)i=0,求x得值.
x=2
3、求以2i-5的虚部为实部,以5i-2的实部为虚部的复数
2-2i
4、设x∈R,则“x=1”是“复数z=(x2-1)+(x+1)i为纯虚数”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
C
解析:由纯虚数的定义知:(x2-1)=0,且x+1≠0,则x=1.
六、课堂小结
(1)说说这节课的收获:你学到了什么?
(2)你还有什么疑惑?你进一步想探究的是什么?
八、作业设计
1、思考:复数集能否进一步扩充?
2、上网搜索复数的发展历史和在科学技术发展中的作用
3、教材P106,习题3.1 题3
谢谢!
