沪教版(上海)数学高二下册-12.5双曲线及其标准方程(课件)(共21张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二下册-12.5双曲线及其标准方程(课件)(共21张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
一、复习回顾
1.双曲线的定义
2.双曲线的标准方程
3.检测练习
二、新课学习
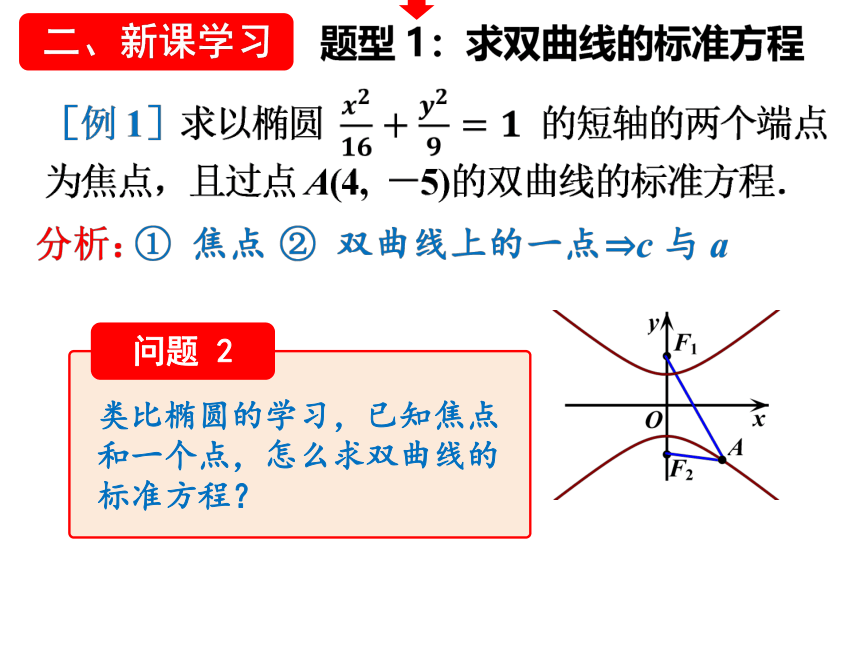
题型1:求双曲线的标准方程
题型2:求轨迹方程
三、总结提升
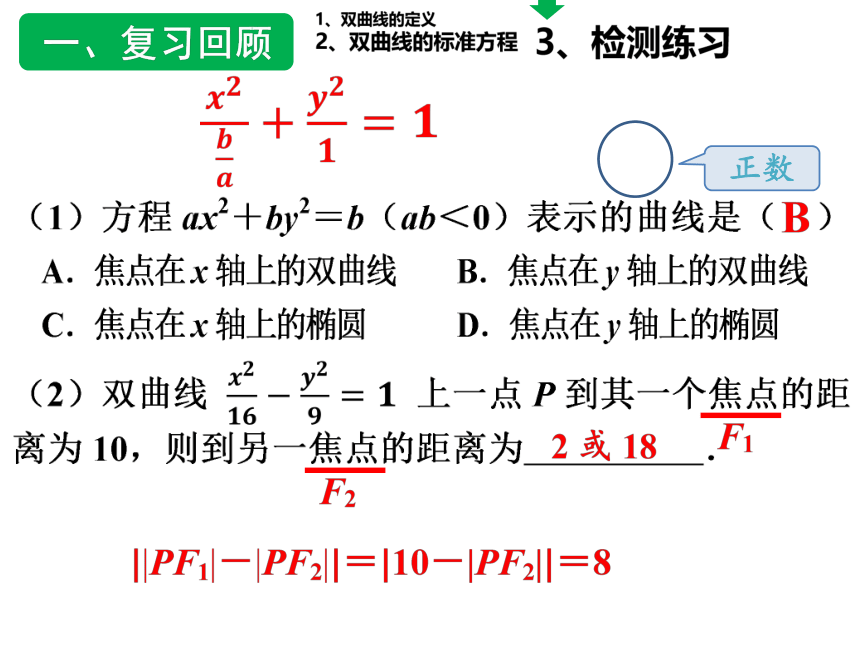
焦点
焦距|F1F2|
把定常数记为2a,
你能用数学符号语言表示双曲线的定义吗?
问题 1
焦点跟着正项走
正数
类比椭圆的学习,已知焦点和一个点,怎么求双曲线的标准方程?
问题 2
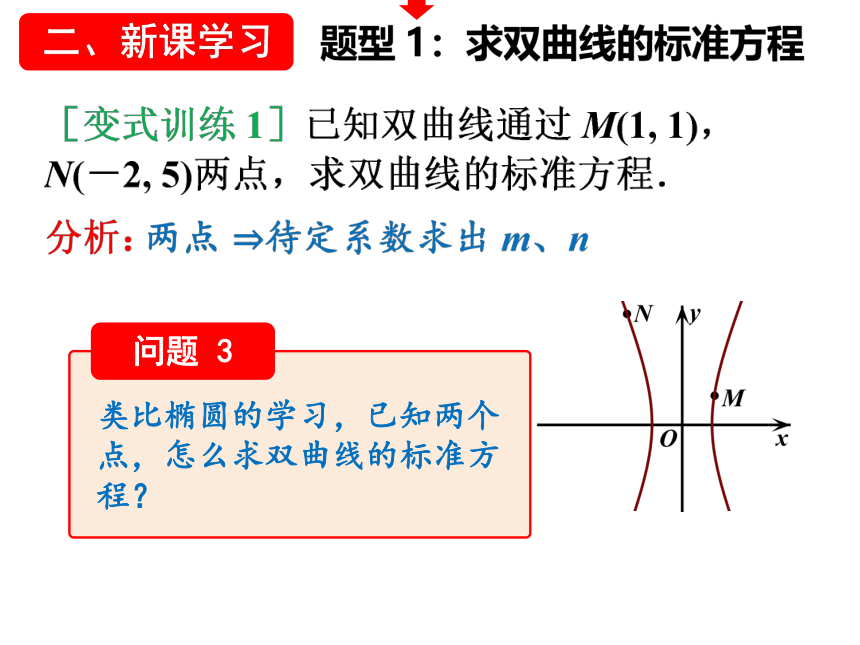
类比椭圆的学习,已知两个点,怎么求双曲线的标准方程?
问题 3
你能小结求双曲线的标准方程的方法吗?
问题 4
求轨迹方程的基本方法是什么?
问题 5
类比椭圆的学习,如果动点和两定点距离有关,怎么求轨迹方程?
问题 6
类比椭圆的学习,如果动点和两定点距离有关,怎么求轨迹方程?
问题 6
如果动圆M与圆C1内切、与圆C2外切,那么动圆圆心M的轨迹是什么?
问题 7
为什么很多同学认为点Q的轨迹是双曲线的一支?你从中得到什么启发?
问题 8
你能小结求轨迹方程的方法吗?
问题 9
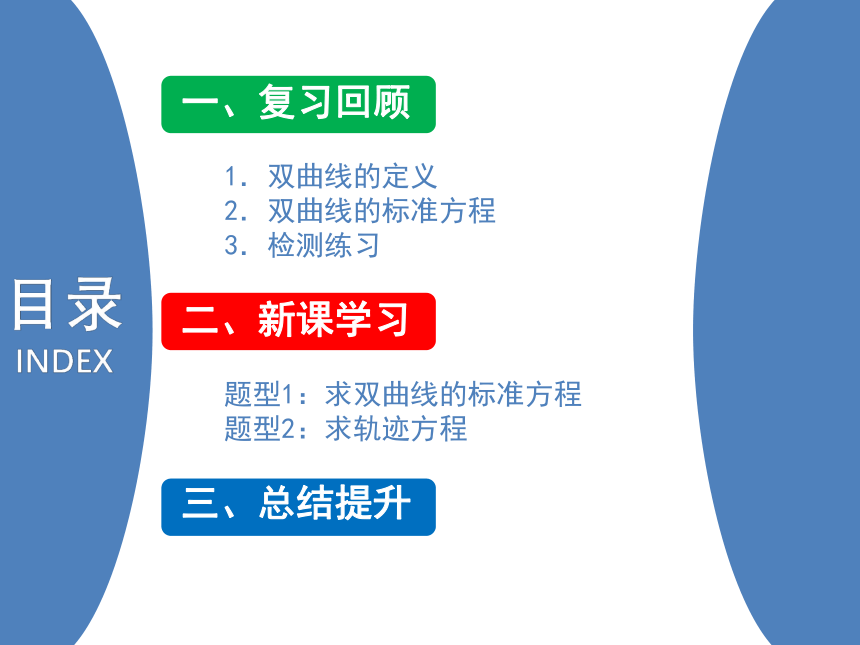
MF1=1114厘米MF2=1095厘米
MF1-MF2=2.0厘米
F1F2=278厘米
目录
INDEX
PF1=261厘米
PF=163厘
P
F
1
o F, x
PF1-PF2=098厘米
O\C
x
二、新课学习题1:求双曲的标准方程题型2:求轨迹方程
变式训练3]已知圆C:(x
2=16,圆C外有一点
A(5,0,P是圆上任意一点,线段AP的垂直平分线l和直线
CP相交于点Q,当点P在圆上运动时,求点Q的轨迹方程
分析:
新课学习题型1求双曲线的标程题型2:求轨迹方程
[变式训练3]已知圆C:(x+5)2+y2=16,圆C外有一点
50),P是圆上任意一点,线段AP的垂直平分线l和直线
CP相交于点Q,当点P在圆上运动时,求点Q的轨迹方程
分析:定点C(-5,0)A(5,0)
四、检测作业
学案P38/变式训练3
2.P39/A级第9题
一、复习回顾
1.双曲线的定义
2.双曲线的标准方程
3.检测练习
二、新课学习
题型1:求双曲线的标准方程
题型2:求轨迹方程
三、总结提升
焦点
焦距|F1F2|
把定常数记为2a,
你能用数学符号语言表示双曲线的定义吗?
问题 1
焦点跟着正项走
正数
类比椭圆的学习,已知焦点和一个点,怎么求双曲线的标准方程?
问题 2
类比椭圆的学习,已知两个点,怎么求双曲线的标准方程?
问题 3
你能小结求双曲线的标准方程的方法吗?
问题 4
求轨迹方程的基本方法是什么?
问题 5
类比椭圆的学习,如果动点和两定点距离有关,怎么求轨迹方程?
问题 6
类比椭圆的学习,如果动点和两定点距离有关,怎么求轨迹方程?
问题 6
如果动圆M与圆C1内切、与圆C2外切,那么动圆圆心M的轨迹是什么?
问题 7
为什么很多同学认为点Q的轨迹是双曲线的一支?你从中得到什么启发?
问题 8
你能小结求轨迹方程的方法吗?
问题 9
MF1=1114厘米MF2=1095厘米
MF1-MF2=2.0厘米
F1F2=278厘米
目录
INDEX
PF1=261厘米
PF=163厘
P
F
1
o F, x
PF1-PF2=098厘米
O\C
x
二、新课学习题1:求双曲的标准方程题型2:求轨迹方程
变式训练3]已知圆C:(x
2=16,圆C外有一点
A(5,0,P是圆上任意一点,线段AP的垂直平分线l和直线
CP相交于点Q,当点P在圆上运动时,求点Q的轨迹方程
分析:
新课学习题型1求双曲线的标程题型2:求轨迹方程
[变式训练3]已知圆C:(x+5)2+y2=16,圆C外有一点
50),P是圆上任意一点,线段AP的垂直平分线l和直线
CP相交于点Q,当点P在圆上运动时,求点Q的轨迹方程
分析:定点C(-5,0)A(5,0)
四、检测作业
学案P38/变式训练3
2.P39/A级第9题
