沪教版(上海)数学高二下册-第11章 坐标平面上的直线 复习(课件)(共38张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二下册-第11章 坐标平面上的直线 复习(课件)(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览









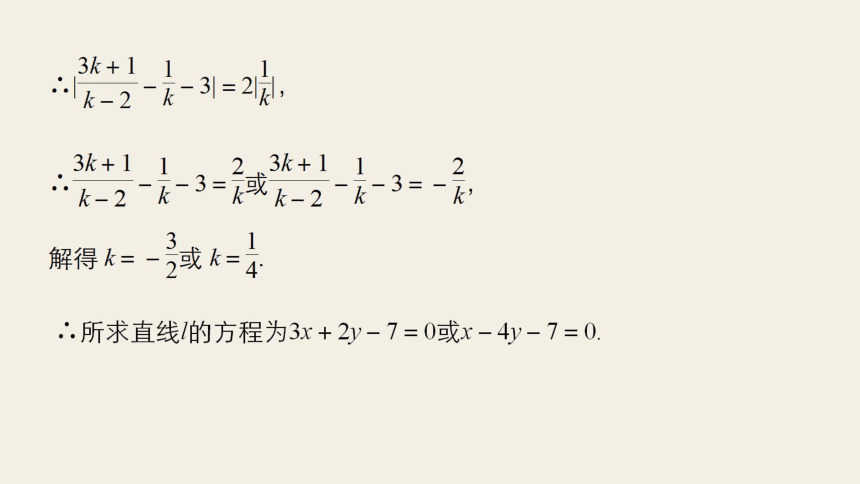

文档简介
(共38张PPT)
第11章 坐标平面上的直线
复习课件
谢 谢
内容索引
知识梳理
题型探究
当堂训练
知识梳理
直线的倾斜角与斜率
(1)直线的倾斜角的范围是0°≤0<180°
(2)当存在时,≠90°;
当k不存在时,=90
(3)斜率的求法
①依据倾斜角;②依据直线方程;③依据两点的坐标、
对对答案吧
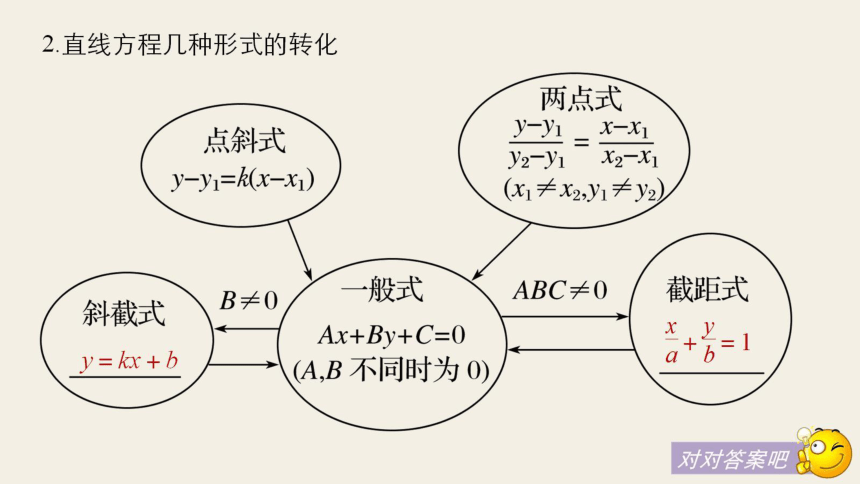
2直线方程几种形式的转化
两点式
点斜式
y-y1 x-x
y2-y1x2-X1
y-1=k(x-xi
(x1≠x2y1≠y2
斜截式\B≠0
般式
ABC≠0/截距式
Ax+By+C=0人
+2=1
y=hx+b
(A,B不同时为0)
a b
对对答案吧
3两条直线的位置关系
设l1:A1+Buy+C1=0,l2:A2x+B+C2=0,则
(1)平行A1B2-A2B1=0且B1C2-B2C1≠0;
(2)相交分A1B2-A2B1≠0;
(重合41=M42,B1=B2,C1=C≠0)或4=B=(4BC2≠0
4距离公式
(1)两点间的距离公式
已知点P1(x1,y1),P2(x2,y2),
则P1P2=1(2=x1)+02-y1
(2)点到直线的距离公式
Axo+ Byo+C
①点P(x,y到直线:Ax+B+C=0的距离=A4+b3
②两平行直线:4+10与2:A++(2=的距离=N42+B2
对对答案吧品
题型探究
类型一待定系数法的应用
例1过点4(3,-1)作直线交x轴于点B,交直线4:y=2x于点C,
若B(1=2B,求直线的方程
解答
解当直线)的斜率不存在时,直线l:x=3,
B(3,0),C(3,6)
此时B(=6,AB=1,BC(≠2AB,
直线斜率存在
设直线的方程为y+1=k(x-3),显然k≠0且k≠2
令y=0,得x
=3+k
B(3+1,0),
y=2x
3k+1
由
y+1=k(x-3,得点C的横坐标x=k2
BC1=2B|,∴kxB-xc=2
3k+1
k-2 k
3k+1
3k+1
k-2A~3
kk-2在~3
二k
解得k=-2或在
所求直线的方程为3x+2y-7=0或x-4y-7=0
反思与感悟
待定系数法,就是所研究的式子(方程)的结构是确定的,但它的全
部或部分系数是待定的,然后根据题中条件来确定这些系数的方法
直线的方程常用待定系数法求解选择合适的直线方程的形式是很
重要的,一般情况下,与截距有关的,可设直线的斜截式方程或截
距式方程;与斜率有关的,可设直线的斜截式或点斜式方程等.
第11章 坐标平面上的直线
复习课件
谢 谢
内容索引
知识梳理
题型探究
当堂训练
知识梳理
直线的倾斜角与斜率
(1)直线的倾斜角的范围是0°≤0<180°
(2)当存在时,≠90°;
当k不存在时,=90
(3)斜率的求法
①依据倾斜角;②依据直线方程;③依据两点的坐标、
对对答案吧
2直线方程几种形式的转化
两点式
点斜式
y-y1 x-x
y2-y1x2-X1
y-1=k(x-xi
(x1≠x2y1≠y2
斜截式\B≠0
般式
ABC≠0/截距式
Ax+By+C=0人
+2=1
y=hx+b
(A,B不同时为0)
a b
对对答案吧
3两条直线的位置关系
设l1:A1+Buy+C1=0,l2:A2x+B+C2=0,则
(1)平行A1B2-A2B1=0且B1C2-B2C1≠0;
(2)相交分A1B2-A2B1≠0;
(重合41=M42,B1=B2,C1=C≠0)或4=B=(4BC2≠0
4距离公式
(1)两点间的距离公式
已知点P1(x1,y1),P2(x2,y2),
则P1P2=1(2=x1)+02-y1
(2)点到直线的距离公式
Axo+ Byo+C
①点P(x,y到直线:Ax+B+C=0的距离=A4+b3
②两平行直线:4+10与2:A++(2=的距离=N42+B2
对对答案吧品
题型探究
类型一待定系数法的应用
例1过点4(3,-1)作直线交x轴于点B,交直线4:y=2x于点C,
若B(1=2B,求直线的方程
解答
解当直线)的斜率不存在时,直线l:x=3,
B(3,0),C(3,6)
此时B(=6,AB=1,BC(≠2AB,
直线斜率存在
设直线的方程为y+1=k(x-3),显然k≠0且k≠2
令y=0,得x
=3+k
B(3+1,0),
y=2x
3k+1
由
y+1=k(x-3,得点C的横坐标x=k2
BC1=2B|,∴kxB-xc=2
3k+1
k-2 k
3k+1
3k+1
k-2A~3
kk-2在~3
二k
解得k=-2或在
所求直线的方程为3x+2y-7=0或x-4y-7=0
反思与感悟
待定系数法,就是所研究的式子(方程)的结构是确定的,但它的全
部或部分系数是待定的,然后根据题中条件来确定这些系数的方法
直线的方程常用待定系数法求解选择合适的直线方程的形式是很
重要的,一般情况下,与截距有关的,可设直线的斜截式方程或截
距式方程;与斜率有关的,可设直线的斜截式或点斜式方程等.
