2021年上海市民办南模学校高二初态考数学试卷(2021.09) (图片版 含答案)
文档属性
| 名称 | 2021年上海市民办南模学校高二初态考数学试卷(2021.09) (图片版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 649.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览


文档简介
南模中学高二初态考数学试卷
1.已知复数z满足z·(1-i)=1+i(i为虚数单位),则|z|=
2.若tan(
3,则t
3.若关于x的方程5=a+3有负实根,则实数a的取值范围是
4.若a、b是异面直线,直线c∥a,则直线b、c的位置关系是
5已知向量AB
(,=),则∠BAC
6.空间不共线的四个点可确定
个平面
7.已知12ina+5cosa可表示为Asin(a+q)(A>0,0≤φ<丌)的形式,则sin2q=
8.将a替换为复数z,以下关于向量模的性质类比到复数中
①|a=a,类比为z
2=|a|,类比为|z2=|z2
③|a+a21|s|a1|+|a2类比为|z1+z2|≤|2|+|z2
④a1·a2≤|al‖a2|,类比为z1·z2≤|z1‖
复数的结论仍成立的序号是
9.设f(x)为奇函数,且在(,0)内是严格减函数,f(2)=0,则J()∠0的解集为
10.设复数z=1-√5在复平面上对应的向量为Oz,将O绕原点O逆时针旋转n个角
后得到向量Oz1(n∈N),向量Oz所对应的复数为z1,若2<0,则自然数n的最小数
值为
设OA|=1,|OB
OB,且A+H=1,则OA在OP
上的数量投影的取值范围是
12.已知函数∫(x)=sinx|+cosx|-4 sinx cos x-k,若函数f(x)在区间(0,z)内恰好有
奇数个零点,则实数k的所有取值之和为
选择题
13.设全集U=C,实数集为R,纯虚数集为M,那么()
A.MUR=UB.MUR=UC.M∩R={0}D.M∩R=R
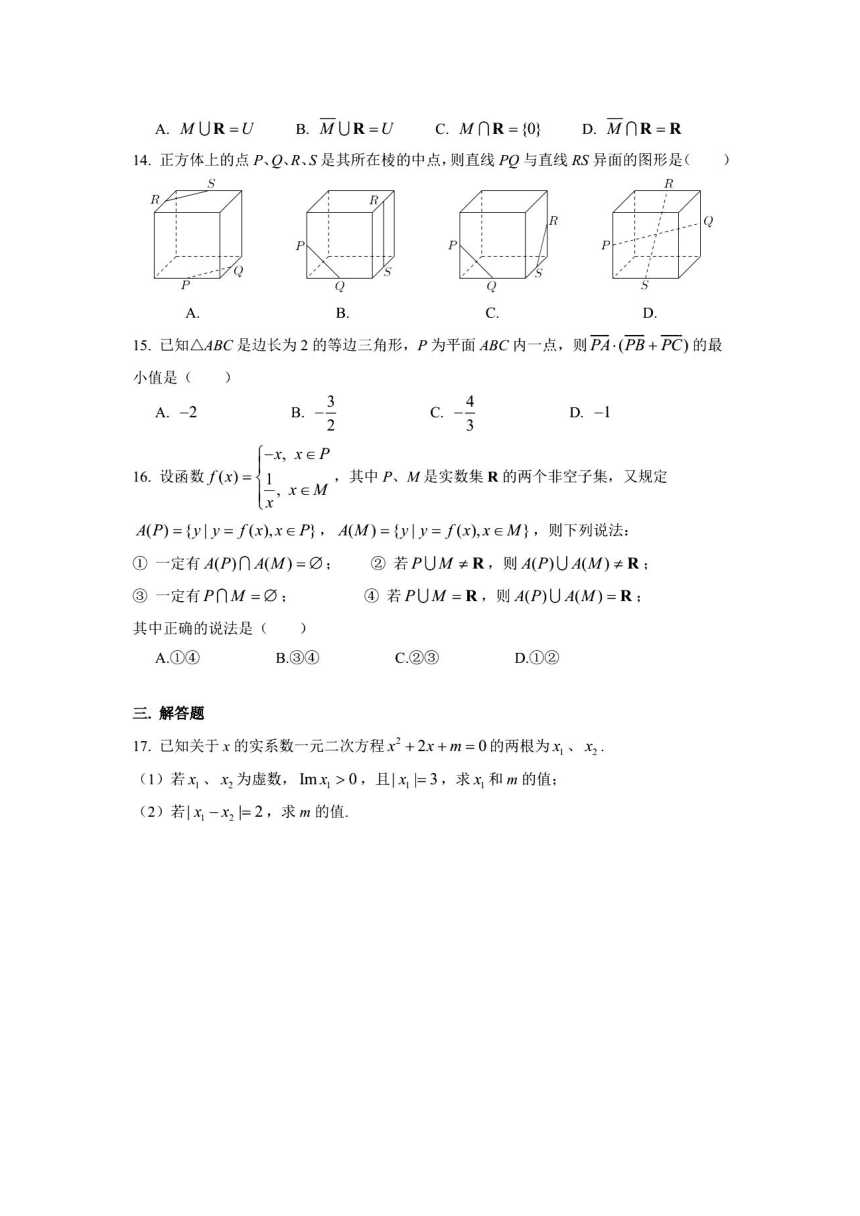
14.正方体上的点P、g、R、S是其所在棱的中点,则直线PQ与直线RS异面的图形是()
15.已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则PA(PB+PC)的最
小值是()
x,x∈
16.设函数f(x)={1
其中P、M是实数集R的两个非空子集,又规定
A(P)={y|y=f(x),x∈P},A(M)={yy=f(x),x∈M},则下列说法:
①一定有A(P∩A(M)=⑧;②若PUM≠R,则A(P)∪A(M)≠R
③一定有P∩M=
④若PUM=R,则A(P)∪A(M)=R
其中正确的说法是()
A.①④
C②③
D①②
三.解答题
17.已知关于x的实系数一元二次方程x2+2x+m=0的两根为x
(1)若x、x2为虚数,Imx,>0,且x}3,求x和m的值:
(2)若|x1-x2|=2,求m的值
1.已知复数z满足z·(1-i)=1+i(i为虚数单位),则|z|=
2.若tan(
3,则t
3.若关于x的方程5=a+3有负实根,则实数a的取值范围是
4.若a、b是异面直线,直线c∥a,则直线b、c的位置关系是
5已知向量AB
(,=),则∠BAC
6.空间不共线的四个点可确定
个平面
7.已知12ina+5cosa可表示为Asin(a+q)(A>0,0≤φ<丌)的形式,则sin2q=
8.将a替换为复数z,以下关于向量模的性质类比到复数中
①|a=a,类比为z
2=|a|,类比为|z2=|z2
③|a+a21|s|a1|+|a2类比为|z1+z2|≤|2|+|z2
④a1·a2≤|al‖a2|,类比为z1·z2≤|z1‖
复数的结论仍成立的序号是
9.设f(x)为奇函数,且在(,0)内是严格减函数,f(2)=0,则J()∠0的解集为
10.设复数z=1-√5在复平面上对应的向量为Oz,将O绕原点O逆时针旋转n个角
后得到向量Oz1(n∈N),向量Oz所对应的复数为z1,若2<0,则自然数n的最小数
值为
设OA|=1,|OB
OB,且A+H=1,则OA在OP
上的数量投影的取值范围是
12.已知函数∫(x)=sinx|+cosx|-4 sinx cos x-k,若函数f(x)在区间(0,z)内恰好有
奇数个零点,则实数k的所有取值之和为
选择题
13.设全集U=C,实数集为R,纯虚数集为M,那么()
A.MUR=UB.MUR=UC.M∩R={0}D.M∩R=R
14.正方体上的点P、g、R、S是其所在棱的中点,则直线PQ与直线RS异面的图形是()
15.已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则PA(PB+PC)的最
小值是()
x,x∈
16.设函数f(x)={1
其中P、M是实数集R的两个非空子集,又规定
A(P)={y|y=f(x),x∈P},A(M)={yy=f(x),x∈M},则下列说法:
①一定有A(P∩A(M)=⑧;②若PUM≠R,则A(P)∪A(M)≠R
③一定有P∩M=
④若PUM=R,则A(P)∪A(M)=R
其中正确的说法是()
A.①④
C②③
D①②
三.解答题
17.已知关于x的实系数一元二次方程x2+2x+m=0的两根为x
(1)若x、x2为虚数,Imx,>0,且x}3,求x和m的值:
(2)若|x1-x2|=2,求m的值
同课章节目录
