23.1图形的旋转(2)同步作业-2021-2022学年人教版九年级上册数学(Word版含答案)
文档属性
| 名称 | 23.1图形的旋转(2)同步作业-2021-2022学年人教版九年级上册数学(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 233.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 12:20:20 | ||
图片预览

文档简介
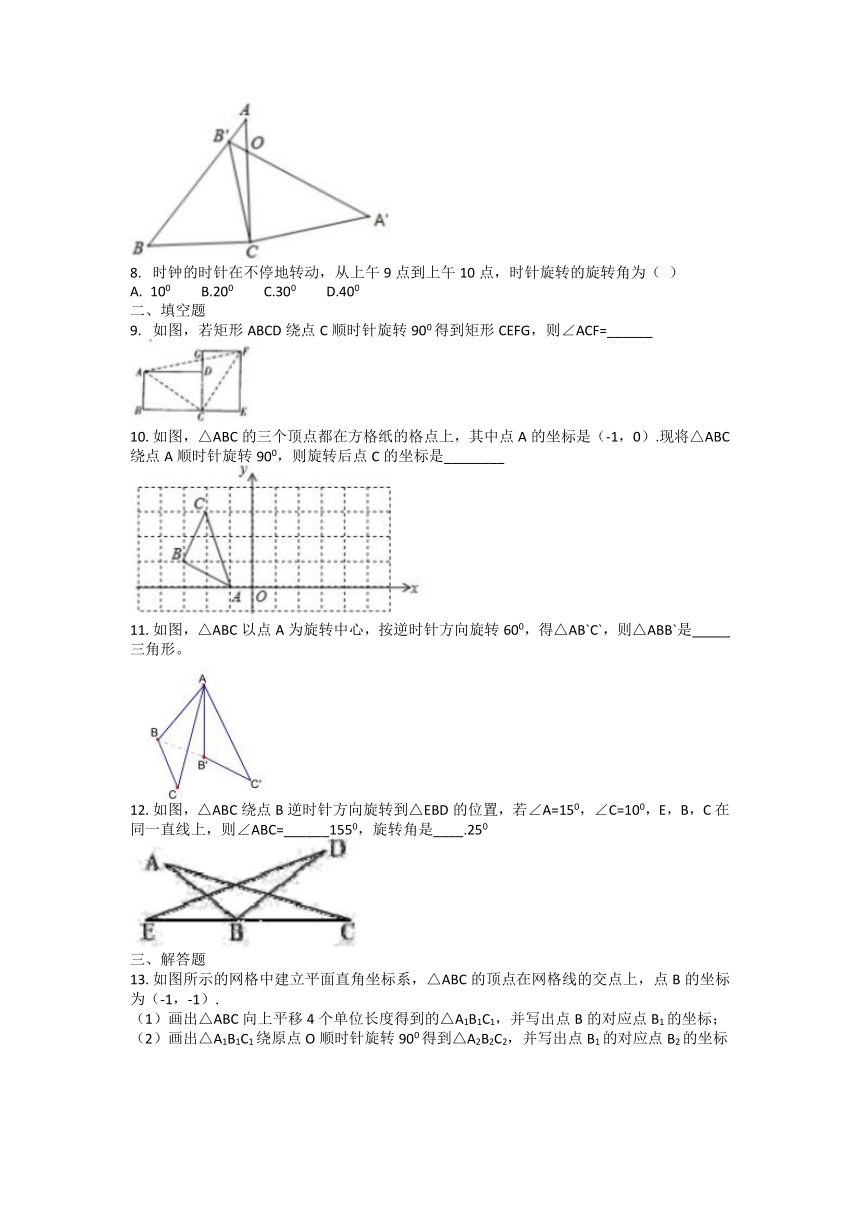
23.1旋转作业(2)
选择题
如图,在Rt△ABC中,∠ACB=900,∠B=600,BC=2. △A`B`C`可以由△ABC绕点C顺时针旋转得到,其中点A`与点A是对应点,点B`与点B是对应点,连结AB`。若A、B`、A`在同一条直线上,则AA`的长为( )
A.6 B. 4 C. D.3
在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转600,得到△BAE,连接ED,若BC=5, BD=4. 则下列结论错误的是( )
△AED的周长=9 B.△BDE是等边三角形 C.∠ADE=∠BDC D.AE∥BC
在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转900得到点P2,则点P2的坐标是( )
(3,-2) B.(2,-3) C.(-3,2) D. (-2,3)
如图,图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
300 B. 600 C. 900 D.1200
如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
100 B.150 C. 200 D. 250
如图,在△ABC中,∠C=900,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
B. C. 3 D.
如图,在三角形ABC中,∠ACB=900, ∠B=500,将此三角形绕点C沿顺时针方向旋转后得到三角形A`B`C`,若点B`恰好落在线段AB上,AC、A`B`交于点O,则∠COA`的度数是( )
500 B.600 C. 700 D.800
时钟的时针在不停地转动,从上午9点到上午10点,时针旋转的旋转角为( )
100 B.200 C.300 D.400
填空题
如图,若矩形ABCD绕点C顺时针旋转900得到矩形CEFG,则∠ACF=______
如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转900,则旋转后点C的坐标是________
如图,△ABC以点A为旋转中心,按逆时针方向旋转600,得△AB`C`,则△ABB`是_____三角形。
如图,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠A=150,∠C=100,E,B,C在同一直线上,则∠ABC=______1550,旋转角是____.250
解答题
如图所示的网格中建立平面直角坐标系,△ABC的顶点在网格线的交点上,点B的坐标为(-1,-1).
画出△ABC向上平移4个单位长度得到的△A1B1C1,并写出点B的对应点B1的坐标;
画出△A1B1C1绕原点O顺时针旋转900得到△A2B2C2,并写出点B1的对应点B2的坐标
如图,在平面直角坐标系xoy中,△A`B`C`由△ABC绕点P旋转得到,求点P的坐标。
15.如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,连接AE,过点A作AF⊥AE交DP于点F,连接BF.
若AF=2,求EF的长。
求证:PF=EP+EB
参考 答案
选择题
A 2.C 3.D 4.C 5.B 6.A 7.B 8.C
填空题
900
(2,1)
11. 等边三角形
12. 1550,250
三、解答题
13.解:(1)如图所示,B1(-1,3);(2)B2(3,1)
14.解:连接AA`、CC`,
作线段AA`的垂直平分线MN,作线段CC`的垂直平分线EF,
直线MN和直线EF的交点这P,点P就是旋转中心。
∵直线MN为x=1,设直线CC`为y=kx+b
由题意得 解得
∴直线
∵直线EF⊥CC`,经过CC`的中点()
∴直线EF为y=-3x+2
当x=1时,y=-3×1+2=-1
∴P(1,-1)
15.解:如图,∵四边形ABCD是正方形,且BE⊥DP, AF⊥AE
∴AB=AD, ∠BAD=∠EAF=∠BEF=900,
∴∠1+∠FAB=∠2+∠FAB=900
∴∠1=∠2
∵∠3+∠5=∠4+∠6=900且∠5=∠6
∴∠3=∠4
∴△ABE≌△AFD
∴AE=AF=2
∴EF=
证明:如图,过点A作AM⊥EF于点M,且∠EAF=900,AE=AF
∴AM=MF=EM,∠AME=∠BEF=900,
∵点P是AB的中点,
∴AP=BP
又∵∠5=∠6,
∴△AMP≌△BFP
∴BE=AM,EP=MP
∴MF=BE
∴PF=PM+FM=EP+EB
选择题
如图,在Rt△ABC中,∠ACB=900,∠B=600,BC=2. △A`B`C`可以由△ABC绕点C顺时针旋转得到,其中点A`与点A是对应点,点B`与点B是对应点,连结AB`。若A、B`、A`在同一条直线上,则AA`的长为( )
A.6 B. 4 C. D.3
在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转600,得到△BAE,连接ED,若BC=5, BD=4. 则下列结论错误的是( )
△AED的周长=9 B.△BDE是等边三角形 C.∠ADE=∠BDC D.AE∥BC
在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转900得到点P2,则点P2的坐标是( )
(3,-2) B.(2,-3) C.(-3,2) D. (-2,3)
如图,图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
300 B. 600 C. 900 D.1200
如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
100 B.150 C. 200 D. 250
如图,在△ABC中,∠C=900,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
B. C. 3 D.
如图,在三角形ABC中,∠ACB=900, ∠B=500,将此三角形绕点C沿顺时针方向旋转后得到三角形A`B`C`,若点B`恰好落在线段AB上,AC、A`B`交于点O,则∠COA`的度数是( )
500 B.600 C. 700 D.800
时钟的时针在不停地转动,从上午9点到上午10点,时针旋转的旋转角为( )
100 B.200 C.300 D.400
填空题
如图,若矩形ABCD绕点C顺时针旋转900得到矩形CEFG,则∠ACF=______
如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转900,则旋转后点C的坐标是________
如图,△ABC以点A为旋转中心,按逆时针方向旋转600,得△AB`C`,则△ABB`是_____三角形。
如图,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠A=150,∠C=100,E,B,C在同一直线上,则∠ABC=______1550,旋转角是____.250
解答题
如图所示的网格中建立平面直角坐标系,△ABC的顶点在网格线的交点上,点B的坐标为(-1,-1).
画出△ABC向上平移4个单位长度得到的△A1B1C1,并写出点B的对应点B1的坐标;
画出△A1B1C1绕原点O顺时针旋转900得到△A2B2C2,并写出点B1的对应点B2的坐标
如图,在平面直角坐标系xoy中,△A`B`C`由△ABC绕点P旋转得到,求点P的坐标。
15.如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,连接AE,过点A作AF⊥AE交DP于点F,连接BF.
若AF=2,求EF的长。
求证:PF=EP+EB
参考 答案
选择题
A 2.C 3.D 4.C 5.B 6.A 7.B 8.C
填空题
900
(2,1)
11. 等边三角形
12. 1550,250
三、解答题
13.解:(1)如图所示,B1(-1,3);(2)B2(3,1)
14.解:连接AA`、CC`,
作线段AA`的垂直平分线MN,作线段CC`的垂直平分线EF,
直线MN和直线EF的交点这P,点P就是旋转中心。
∵直线MN为x=1,设直线CC`为y=kx+b
由题意得 解得
∴直线
∵直线EF⊥CC`,经过CC`的中点()
∴直线EF为y=-3x+2
当x=1时,y=-3×1+2=-1
∴P(1,-1)
15.解:如图,∵四边形ABCD是正方形,且BE⊥DP, AF⊥AE
∴AB=AD, ∠BAD=∠EAF=∠BEF=900,
∴∠1+∠FAB=∠2+∠FAB=900
∴∠1=∠2
∵∠3+∠5=∠4+∠6=900且∠5=∠6
∴∠3=∠4
∴△ABE≌△AFD
∴AE=AF=2
∴EF=
证明:如图,过点A作AM⊥EF于点M,且∠EAF=900,AE=AF
∴AM=MF=EM,∠AME=∠BEF=900,
∵点P是AB的中点,
∴AP=BP
又∵∠5=∠6,
∴△AMP≌△BFP
∴BE=AM,EP=MP
∴MF=BE
∴PF=PM+FM=EP+EB
同课章节目录
