12.1 全等三角形 课时作业(含答案)
文档属性
| 名称 | 12.1 全等三角形 课时作业(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 327.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 02:31:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上册课时作业
第十二章 全等三角形
12.1 全等三角形
一、选择题
1. 下列说法正确的是( )
A.两个面积相等的图形一定是全等图形 B.两个长方形是全等图形
C.两个全等图形形状一定相同 D.两个正方形一定是全等图形
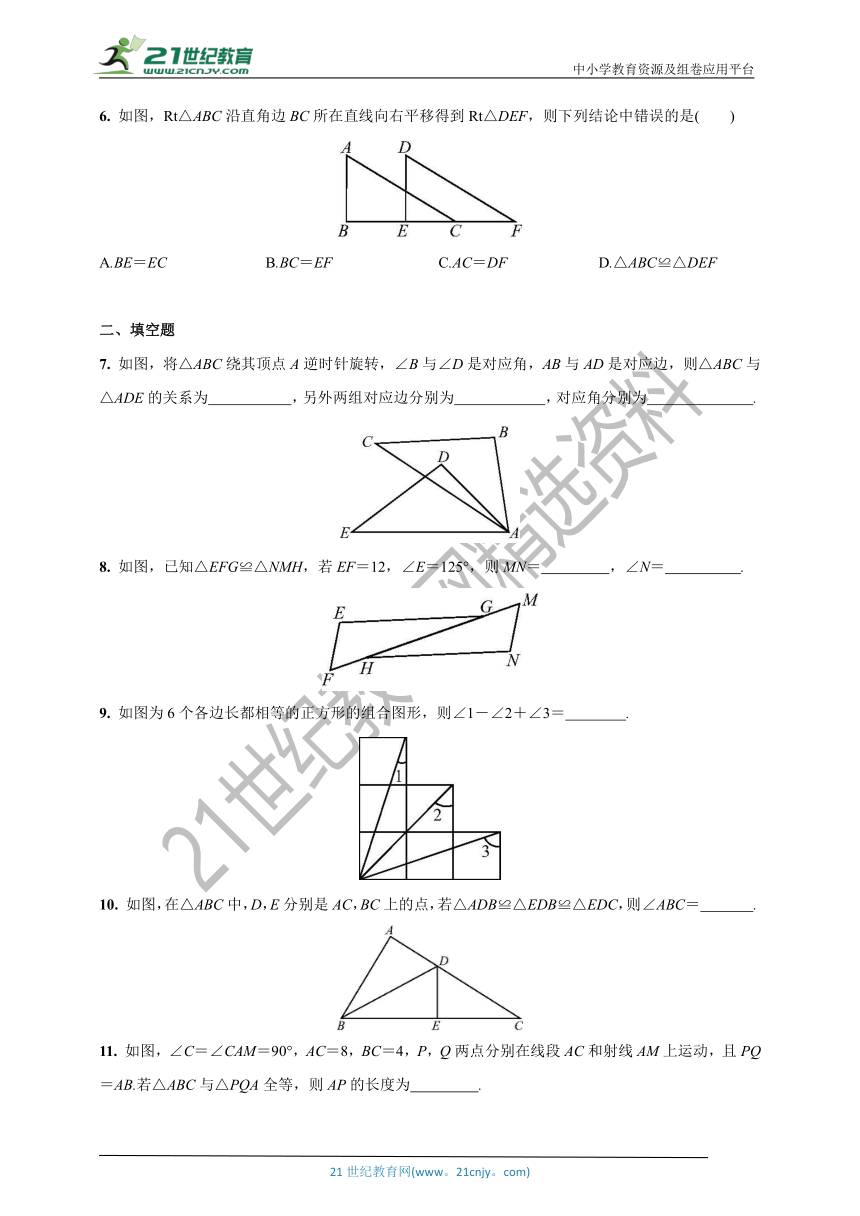
2. 如图,已知△ABC≌△DEF,BC∥EF,AC∥DF,则∠C的对应角是( )
A.∠F B.∠AGF C.∠AEF D.∠D
3. 如图,△ABD≌△CDB,则AB的长是( )
A.AD B.CD C.BC D.BD
4. 如图,已知△ABC≌△ABD,若∠BAC=55°,则∠CAD的度数是( )
A.115° B.110° C.105° D.100°
5. 已知图中的两个三角形全等,图中的字母表示三角形的边长,则∠1等于( )
A.72° B.60° C.58° D.50°
6. 如图,Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,则下列结论中错误的是( )
A.BE=EC B.BC=EF C.AC=DF D.△ABC≌△DEF
二、填空题
7. 如图,将△ABC绕其顶点A逆时针旋转,∠B与∠D是对应角,AB与AD是对应边,则△ABC与△ADE的关系为 ,另外两组对应边分别为 ,对应角分别为 .
8. 如图,已知△EFG≌△NMH,若EF=12,∠E=125°,则MN= ,∠N= .
9. 如图为6个各边长都相等的正方形的组合图形,则∠1-∠2+∠3= .
10. 如图,在△ABC中,D,E分别是AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠ABC= .
11. 如图,∠C=∠CAM=90°,AC=8,BC=4,P,Q两点分别在线段AC和射线AM上运动,且PQ=AB.若△ABC与△PQA全等,则AP的长度为 .
三、解答题
12. 如图,已知△ADF≌△CBE,点E,B,D,F在同一条直线上.
(1)线段AD与BC之间的数量关系是 ,其数学依据是 ;
(2)判断AD与BC之间的位置关系,并说明理由.
13. 如图,已知△ACF≌△DBE,AD=11,BC=7.
(1)试说明:AB=CD;
(2)求线段AB的长.
14. 如图,已知△ABE≌△ACD.
(1)如果BE=6,DE=2,求BC的长;
(2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数.
15. 如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)证明:BD=DE+CE.
(2)当△ABD满足什么条件时,BD∥CE
参考答案
1. C 2. A 3. B 4. B 5. C 6. A
7. △ABC≌△ADE AC和AE,BC和DE ∠C和∠E,∠BAC和∠DAE 8. 12 125° 9. 45° 10. 60° 11. 4或8
12. 解:(1)AD=BC 全等三角形的对应边相等
(2)AD∥BC. 理由:略.
13. 解:(1)∵△ACF≌△DBE,∴AC=DB,∴AC-BC=DB-BC,即AB=CD.
(2)∵AD=11,BC=7,∴AB=(AD-BC)=×(11-7)=2.
14. 解:(1)∵△ABE≌△ACD,∴BE=CD. ∵BE=6,DE=2,∴CE=4. ∴BC=BE+CE=6+4=10.
(2)∵△ABE≌△ACD,∴∠BAE=∠CAD. ∵∠BAC=75°,∠BAD=30°,∴∠BAE=∠CAD=45°,∴∠DAE=∠CAD-∠CAE=45°-30°=15°.
15. 解:(1)∵△BAD≌△ACE,∴BD=AE,AD=CE,又∵AE=AD+DE=CE+DE,∴BD=DE+CE.
(2)△ABD满足∠ADB=90°时,BD∥CE. ∵△BAD≌△ACE,∴∠ADB=∠CEA. 若BD∥CE,则∠CED=∠BDE,∴∠ADB=∠BDE,又∵∠ADB+∠BDE=180°,∴∠ADB=90°.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
人教版八年级数学上册课时作业
第十二章 全等三角形
12.1 全等三角形
一、选择题
1. 下列说法正确的是( )
A.两个面积相等的图形一定是全等图形 B.两个长方形是全等图形
C.两个全等图形形状一定相同 D.两个正方形一定是全等图形
2. 如图,已知△ABC≌△DEF,BC∥EF,AC∥DF,则∠C的对应角是( )
A.∠F B.∠AGF C.∠AEF D.∠D
3. 如图,△ABD≌△CDB,则AB的长是( )
A.AD B.CD C.BC D.BD
4. 如图,已知△ABC≌△ABD,若∠BAC=55°,则∠CAD的度数是( )
A.115° B.110° C.105° D.100°
5. 已知图中的两个三角形全等,图中的字母表示三角形的边长,则∠1等于( )
A.72° B.60° C.58° D.50°
6. 如图,Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,则下列结论中错误的是( )
A.BE=EC B.BC=EF C.AC=DF D.△ABC≌△DEF
二、填空题
7. 如图,将△ABC绕其顶点A逆时针旋转,∠B与∠D是对应角,AB与AD是对应边,则△ABC与△ADE的关系为 ,另外两组对应边分别为 ,对应角分别为 .
8. 如图,已知△EFG≌△NMH,若EF=12,∠E=125°,则MN= ,∠N= .
9. 如图为6个各边长都相等的正方形的组合图形,则∠1-∠2+∠3= .
10. 如图,在△ABC中,D,E分别是AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠ABC= .
11. 如图,∠C=∠CAM=90°,AC=8,BC=4,P,Q两点分别在线段AC和射线AM上运动,且PQ=AB.若△ABC与△PQA全等,则AP的长度为 .
三、解答题
12. 如图,已知△ADF≌△CBE,点E,B,D,F在同一条直线上.
(1)线段AD与BC之间的数量关系是 ,其数学依据是 ;
(2)判断AD与BC之间的位置关系,并说明理由.
13. 如图,已知△ACF≌△DBE,AD=11,BC=7.
(1)试说明:AB=CD;
(2)求线段AB的长.
14. 如图,已知△ABE≌△ACD.
(1)如果BE=6,DE=2,求BC的长;
(2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数.
15. 如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)证明:BD=DE+CE.
(2)当△ABD满足什么条件时,BD∥CE
参考答案
1. C 2. A 3. B 4. B 5. C 6. A
7. △ABC≌△ADE AC和AE,BC和DE ∠C和∠E,∠BAC和∠DAE 8. 12 125° 9. 45° 10. 60° 11. 4或8
12. 解:(1)AD=BC 全等三角形的对应边相等
(2)AD∥BC. 理由:略.
13. 解:(1)∵△ACF≌△DBE,∴AC=DB,∴AC-BC=DB-BC,即AB=CD.
(2)∵AD=11,BC=7,∴AB=(AD-BC)=×(11-7)=2.
14. 解:(1)∵△ABE≌△ACD,∴BE=CD. ∵BE=6,DE=2,∴CE=4. ∴BC=BE+CE=6+4=10.
(2)∵△ABE≌△ACD,∴∠BAE=∠CAD. ∵∠BAC=75°,∠BAD=30°,∴∠BAE=∠CAD=45°,∴∠DAE=∠CAD-∠CAE=45°-30°=15°.
15. 解:(1)∵△BAD≌△ACE,∴BD=AE,AD=CE,又∵AE=AD+DE=CE+DE,∴BD=DE+CE.
(2)△ABD满足∠ADB=90°时,BD∥CE. ∵△BAD≌△ACE,∴∠ADB=∠CEA. 若BD∥CE,则∠CED=∠BDE,∴∠ADB=∠BDE,又∵∠ADB+∠BDE=180°,∴∠ADB=90°.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
