3.4一元一次方程模型的应用(1)湘教版数学七年级上册 课件(20张)
文档属性
| 名称 | 3.4一元一次方程模型的应用(1)湘教版数学七年级上册 课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 145.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 12:09:13 | ||
图片预览








文档简介
(共20张PPT)
3.4一元一次方程模型的应用(1)
第1课时和、差、倍、分问题
1.比a的三倍大5的数: ____________
3.比x大5的数 : __________
4. y的三分之一的数 : ___________
5. x的2倍与10的和的数: ________
2.x的四分之一减y的差的数 :_____________
列出下列代数式
x+5
2x+10
知识回顾
新课讲授
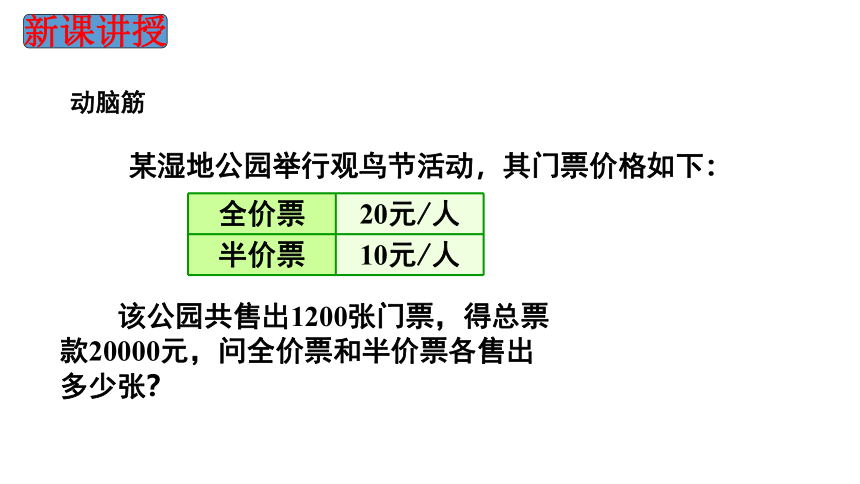
动脑筋
某湿地公园举行观鸟节活动,其门票价格如下:
全价票 20元/人
半价票 10元/人
该公园共售出1200张门票,得总票款20000元,问全价票和半价票各售出多少张?
解:设售出全价票x张,
根据等量关系,建立一元一次方程,得
20x+(1200-x)·10=20000 .
去括号,得20x+12000-10x=20000.
移项,合并同类项,得10x=8000.
即 x=800.
半价票为 1200-800=400(张).
答:全价票售出800张,半价票售出400张.
本问题中涉及的等量关系有:
①全价票售出的张数+半价票售出的张数=1200张
②全价票款+半价票款 = 20000元.
全价票的张数×票价
半价票的张数×票价
+
↓
↓
则售出半价票(1200-x)张.
我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何.”其大意是:有若干只鸡和兔关在同一笼子里,它们一共有35个头,94条腿.问笼中的鸡和兔各有多少只?请用列方程解应用题的方法求出问题的解
由题意可知,本题涉及的等量关系如下:
②鸡的腿数十免的腿数=94
①鸡的只数十兔的只数=35;
根据题意,得
2x+4(35-x)=94.
解方程,得x=23
所以35-x=35-23=12
答:笼中的鸡有23只,兔有12只
②鸡的腿数十免的腿数=94
①鸡的只数十兔的只数=35;
解:设笼中的鸡有x只,则兔有(35-x)只.
1.练习本比水性笔的单价少2元,小刚买了5本练习本和3支水性笔正好用去14元,如果设水性笔的单价为x元,那么下列方程正确的是( ).
A.5(x-2)+3x=14
B.5(x+2)+3x=14
C.5x+3(x+2)=14
D.5x+3(x-2)=14
2.在“爱护环境,建设家乡”的活动中,九年级一班学生回收饮料瓶共20kg,女生回收的质量是男生的一半.设女生回收饮料瓶xkg.根据题意,可列方知程为( )
A.2(20-x)=x B
C.2x=20+x D.2x=20-x
基础巩固
A
等量关系:
水性笔的单价-2=练习本的单价
5本练习本的费用+3支水性笔的费用=14元
等量关系:
女生回收的质量= ×男生回收的质量
女生回收的质量+男生回收的质量=20 kg
D
3.甲班有54人,乙班有48人,要使甲班人数是乙班人数的2倍,设从乙班调往甲班x人,可列方程_________.
4.孙子问爷爷:“您今年多大年龄了啊?”爷爷说:“如果我再活现在岁数的三分之一,加上4岁,正好是100岁。”设爷爷现在x岁可列方程_________
分析 本问题中涉及的等量关系有:
甲班调进后的人数=乙班调出后的人数×2
54+x=2(48-x)
分析 本问题中涉及的等量关系有:
爷爷现在的年龄+ ×爷爷现在的年龄+4=100
5.足球比赛的记分规则是:胜一场得3分,平一场得1分,负一场得0分. 某队在某次比赛中共踢了14场球,其中负5场,共得19分. 问这个队共胜了多少场.
答:这个队共胜了5场.
解:设共胜利x场,则平(14-5-x)场
根据题意,得3x+1×(9-x)+0×5=19
解得 x=5
分析 本问题中涉及的等量关系有:
②胜场得的分数+负场得的分数+平场得的分数=总分
①胜的场数+平的场数+负的场数=14 场
6.(黄冈中考)在红城中学举行“我爱祖国”征文活动中,七年级和
八年级共收到征文118篇,且七年级收到的征文篇数比八年级收
到的征文篇数的一半还少2篇.求七年级收到的征文有多少篇
等量关系:①七年级征文篇数+八年级征文篇数=118篇
②七年级征文篇数=
分析 本问题中涉及的等量关系有:
能力提升
解:设七年级收到的征文有x篇,则八年级收到的征文有(118-x)篇
根据题意,得
答:七年级收到的征文有38篇.
等量关系:①七年级征文篇数+八年级征文篇数=118篇
②七年级征文篇数=
7.某种中药含有甲、乙、丙、丁四种草药成分,其质量比是0.7∶1∶2∶4.7,现要配制这种中药2100克,四种草药分别需要多少克?
分析 本问题中涉及的等量关系有:
甲种成分的质量+乙种成分的质量+丙种成分的质量+丁种成分的质量=总质量
解:设需要甲种草药0.7x克,乙种草药x克,丙种草药2x克,丁种草药4.7x克,
根据题意,得0.7x+x+2x+4.7x=2100.
解得x=250,
所以0.7x=175,2x=500,4.7x=1175.
答:需要甲种草药175克,乙种草药250克,丙种草药500克,丁种草药1175克.
拓展提升
翻页
【归纳总结】比例问题中的全部数量=各种成分的数量值之和.一般设其中的一份为x.
8.在手工制作课上,老师组织初一(2)班的学生用硬纸制作圆柱形茶叶筒.初一(2)班共有学生45人,其中男生的人数比女生人数的2倍少24人,并且每名学生每小时剪筒身60个或剪筒底150个
(1)初一(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
分析 本问题中涉及的等量关系有:
(1)男生的人数+女生的人数=45人
男生的人数=2 ×女生的人数-24
解:(1)设初一(2)班有女生x人
依据题意得出x+(2x-24)=45,
解得x=23,
则45-23=22,
答:初一(2)班有男生22人、女生23人
翻页
依据题意得60x X 2=150(45-x),
解得x=25,
则45-25=20
答:应该分配剪简身的学生为25人,分配剪简底的为20人
8.在手工制作课上,老师组织初一(2)班的学生用硬纸制作圆柱形茶叶筒.初一(2)班共有学生45人,其中男生的人数比女生人数的2倍少24人,并且每名学生每小时剪筒身60个或剪筒底150个
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
分析 本问题中涉及的等量关系有:
每小时剪出的筒身的数量×2=每小时剪出的筒底的数量
解(2)设分配剪筒身的学生为x人,
翻页
9.已知甲、乙两桶内共有水48kg,如果甲桶给乙桶加水,使乙桶的水增加1倍,然后乙桶又给甲桶加水,为甲桶剩余的水的一倍,此时两桶内水的质量相等,问:甲乙两桶内原有多少水?
分析 本问题中涉及的等量关系有:
甲桶水第二次变化后的质量=乙桶水第二次变化后的质量
甲桶水的质量+乙桶水的质量=总质量
分析:设甲桶内原有水x kg,则乙桶内原有水(48-x)kg
第一次加水:甲桶内剩余水:x-(48-x)
乙桶内水:
2(48-x)
第二次加水:甲桶内水:2﹝x-(48-x)﹞
乙桶内剩余水:
2(48-x)-﹝x-(48-x)﹞
解:设甲桶内原有水x kg,则乙桶内原有水(48-x)kg
由题意得:2﹝x-(48-x)﹞=2(48-x)-﹝x-(48-x)﹞
解得x=30
因此,乙桶内原有水48-x=48-30=28(kg)
答:甲桶内原有水30kg,则乙桶内原有水18kg
运用一元一次方程模型解决实际问题的步骤有哪些?
总结提升
归纳:
实际问题
建立方程模型
解方程
检验解的
合理性
分析等量关系
设未知数
作答
1.出操时,初一、初二两个方队共有学生146人,如果让初一方队中的11人插到初二方队,那么两个方队的人数相等.初一初二方队原来各有多少人?
作业布置
2.甲、乙、丙三个村庄合修一条水渠,计划需要176个劳动力,由于各村人口多少不等,只有按2:3:6的比例摊派才较合理,问甲、乙、丙三个村庄各派出多少个劳动力?
3.大、小两台拖拉机一天共耕地19公顷.其中大拖拉机耕地的面积比小拖拉机耕地面积的2倍还多1公顷,这两台拖拉机一天各耕地多少公顷?
3.4一元一次方程模型的应用(1)
第1课时和、差、倍、分问题
1.比a的三倍大5的数: ____________
3.比x大5的数 : __________
4. y的三分之一的数 : ___________
5. x的2倍与10的和的数: ________
2.x的四分之一减y的差的数 :_____________
列出下列代数式
x+5
2x+10
知识回顾
新课讲授
动脑筋
某湿地公园举行观鸟节活动,其门票价格如下:
全价票 20元/人
半价票 10元/人
该公园共售出1200张门票,得总票款20000元,问全价票和半价票各售出多少张?
解:设售出全价票x张,
根据等量关系,建立一元一次方程,得
20x+(1200-x)·10=20000 .
去括号,得20x+12000-10x=20000.
移项,合并同类项,得10x=8000.
即 x=800.
半价票为 1200-800=400(张).
答:全价票售出800张,半价票售出400张.
本问题中涉及的等量关系有:
①全价票售出的张数+半价票售出的张数=1200张
②全价票款+半价票款 = 20000元.
全价票的张数×票价
半价票的张数×票价
+
↓
↓
则售出半价票(1200-x)张.
我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何.”其大意是:有若干只鸡和兔关在同一笼子里,它们一共有35个头,94条腿.问笼中的鸡和兔各有多少只?请用列方程解应用题的方法求出问题的解
由题意可知,本题涉及的等量关系如下:
②鸡的腿数十免的腿数=94
①鸡的只数十兔的只数=35;
根据题意,得
2x+4(35-x)=94.
解方程,得x=23
所以35-x=35-23=12
答:笼中的鸡有23只,兔有12只
②鸡的腿数十免的腿数=94
①鸡的只数十兔的只数=35;
解:设笼中的鸡有x只,则兔有(35-x)只.
1.练习本比水性笔的单价少2元,小刚买了5本练习本和3支水性笔正好用去14元,如果设水性笔的单价为x元,那么下列方程正确的是( ).
A.5(x-2)+3x=14
B.5(x+2)+3x=14
C.5x+3(x+2)=14
D.5x+3(x-2)=14
2.在“爱护环境,建设家乡”的活动中,九年级一班学生回收饮料瓶共20kg,女生回收的质量是男生的一半.设女生回收饮料瓶xkg.根据题意,可列方知程为( )
A.2(20-x)=x B
C.2x=20+x D.2x=20-x
基础巩固
A
等量关系:
水性笔的单价-2=练习本的单价
5本练习本的费用+3支水性笔的费用=14元
等量关系:
女生回收的质量= ×男生回收的质量
女生回收的质量+男生回收的质量=20 kg
D
3.甲班有54人,乙班有48人,要使甲班人数是乙班人数的2倍,设从乙班调往甲班x人,可列方程_________.
4.孙子问爷爷:“您今年多大年龄了啊?”爷爷说:“如果我再活现在岁数的三分之一,加上4岁,正好是100岁。”设爷爷现在x岁可列方程_________
分析 本问题中涉及的等量关系有:
甲班调进后的人数=乙班调出后的人数×2
54+x=2(48-x)
分析 本问题中涉及的等量关系有:
爷爷现在的年龄+ ×爷爷现在的年龄+4=100
5.足球比赛的记分规则是:胜一场得3分,平一场得1分,负一场得0分. 某队在某次比赛中共踢了14场球,其中负5场,共得19分. 问这个队共胜了多少场.
答:这个队共胜了5场.
解:设共胜利x场,则平(14-5-x)场
根据题意,得3x+1×(9-x)+0×5=19
解得 x=5
分析 本问题中涉及的等量关系有:
②胜场得的分数+负场得的分数+平场得的分数=总分
①胜的场数+平的场数+负的场数=14 场
6.(黄冈中考)在红城中学举行“我爱祖国”征文活动中,七年级和
八年级共收到征文118篇,且七年级收到的征文篇数比八年级收
到的征文篇数的一半还少2篇.求七年级收到的征文有多少篇
等量关系:①七年级征文篇数+八年级征文篇数=118篇
②七年级征文篇数=
分析 本问题中涉及的等量关系有:
能力提升
解:设七年级收到的征文有x篇,则八年级收到的征文有(118-x)篇
根据题意,得
答:七年级收到的征文有38篇.
等量关系:①七年级征文篇数+八年级征文篇数=118篇
②七年级征文篇数=
7.某种中药含有甲、乙、丙、丁四种草药成分,其质量比是0.7∶1∶2∶4.7,现要配制这种中药2100克,四种草药分别需要多少克?
分析 本问题中涉及的等量关系有:
甲种成分的质量+乙种成分的质量+丙种成分的质量+丁种成分的质量=总质量
解:设需要甲种草药0.7x克,乙种草药x克,丙种草药2x克,丁种草药4.7x克,
根据题意,得0.7x+x+2x+4.7x=2100.
解得x=250,
所以0.7x=175,2x=500,4.7x=1175.
答:需要甲种草药175克,乙种草药250克,丙种草药500克,丁种草药1175克.
拓展提升
翻页
【归纳总结】比例问题中的全部数量=各种成分的数量值之和.一般设其中的一份为x.
8.在手工制作课上,老师组织初一(2)班的学生用硬纸制作圆柱形茶叶筒.初一(2)班共有学生45人,其中男生的人数比女生人数的2倍少24人,并且每名学生每小时剪筒身60个或剪筒底150个
(1)初一(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
分析 本问题中涉及的等量关系有:
(1)男生的人数+女生的人数=45人
男生的人数=2 ×女生的人数-24
解:(1)设初一(2)班有女生x人
依据题意得出x+(2x-24)=45,
解得x=23,
则45-23=22,
答:初一(2)班有男生22人、女生23人
翻页
依据题意得60x X 2=150(45-x),
解得x=25,
则45-25=20
答:应该分配剪简身的学生为25人,分配剪简底的为20人
8.在手工制作课上,老师组织初一(2)班的学生用硬纸制作圆柱形茶叶筒.初一(2)班共有学生45人,其中男生的人数比女生人数的2倍少24人,并且每名学生每小时剪筒身60个或剪筒底150个
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
分析 本问题中涉及的等量关系有:
每小时剪出的筒身的数量×2=每小时剪出的筒底的数量
解(2)设分配剪筒身的学生为x人,
翻页
9.已知甲、乙两桶内共有水48kg,如果甲桶给乙桶加水,使乙桶的水增加1倍,然后乙桶又给甲桶加水,为甲桶剩余的水的一倍,此时两桶内水的质量相等,问:甲乙两桶内原有多少水?
分析 本问题中涉及的等量关系有:
甲桶水第二次变化后的质量=乙桶水第二次变化后的质量
甲桶水的质量+乙桶水的质量=总质量
分析:设甲桶内原有水x kg,则乙桶内原有水(48-x)kg
第一次加水:甲桶内剩余水:x-(48-x)
乙桶内水:
2(48-x)
第二次加水:甲桶内水:2﹝x-(48-x)﹞
乙桶内剩余水:
2(48-x)-﹝x-(48-x)﹞
解:设甲桶内原有水x kg,则乙桶内原有水(48-x)kg
由题意得:2﹝x-(48-x)﹞=2(48-x)-﹝x-(48-x)﹞
解得x=30
因此,乙桶内原有水48-x=48-30=28(kg)
答:甲桶内原有水30kg,则乙桶内原有水18kg
运用一元一次方程模型解决实际问题的步骤有哪些?
总结提升
归纳:
实际问题
建立方程模型
解方程
检验解的
合理性
分析等量关系
设未知数
作答
1.出操时,初一、初二两个方队共有学生146人,如果让初一方队中的11人插到初二方队,那么两个方队的人数相等.初一初二方队原来各有多少人?
作业布置
2.甲、乙、丙三个村庄合修一条水渠,计划需要176个劳动力,由于各村人口多少不等,只有按2:3:6的比例摊派才较合理,问甲、乙、丙三个村庄各派出多少个劳动力?
3.大、小两台拖拉机一天共耕地19公顷.其中大拖拉机耕地的面积比小拖拉机耕地面积的2倍还多1公顷,这两台拖拉机一天各耕地多少公顷?
同课章节目录
