3.2.2奇偶性(第2课时)课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共23张PPT)
文档属性
| 名称 | 3.2.2奇偶性(第2课时)课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 21:57:46 | ||
图片预览







文档简介
(共23张PPT)
3.2 函数的基本性质
3.2.2 奇偶性
第2课时
复习与回顾
1.什么是奇函数,偶函数?它们的特征各是怎样的?
(1)图象法(直观判断);
(2)定义法(严格推导)。
2.如何判定一个函数的奇偶性?
3.函数的单调性和奇偶性各反应了函数怎样的性质?
单调性反映的是函数的增减性,奇偶性反映的是函数的对称性;
单调性针对的是定义域下的某一个区间,奇偶性针对的是整个定义域。
新课
2.奇偶函数的特征:
对于奇函数有:f(-x)=-f(x)
一般地,设函数f(x)的定义域为Ⅰ,
如果 x∈Ⅰ,都有-x∈Ⅰ,且
f(-x)=-f(x)
那么函数f(x)就叫做奇函数(evenfunction).
如果 x∈Ⅰ,都有-x∈Ⅰ,且
f(-x)=f(x)
那么函数f(x)就叫做偶函数(evenfunction).
1. 定义
函数的奇偶性
奇函数图象关于原点对称;
(2)代数特征:
(3)几何特征:
(1)定义域特征:
定义域关于原点对称.
(自变量取一对相反数时,函数值也是一对相反数)
返回
(或f(-x)+f(x)=0)
(或f(-x)-f(x)=0)
对于偶函数有:f(-x)=f(x)
偶函数图象关于y轴对称.
(自变量取一对相反数时,函数值相等)
(1)求函数的定义域Ⅰ;
(2)判断定义域Ⅰ是否关于原点对称;
若定义域Ⅰ关于原点对称,则函数不具有奇偶性;
若定义域Ⅰ关于原点对称关于原点对称,则进入第三步.
(3) x∈Ⅰ,计算f(-x),并判断f(-x)与f(x)的关系;
(4)作结论.
若f(-x)=-f(x),则函数是奇函数;
若f(-x)=f(x),则函数是偶函数;
若f(-x)≠f(x)且f(-x)=-f(x) ,则f(x)既非奇函数又非偶函数;
若f(-x)=f(x)且f(-x)=-f(x) ,则f(x)既是奇函数又是偶函数.
用定义法判定函数f(x)的奇偶性的步骤
返回
一求二看
三算
四断
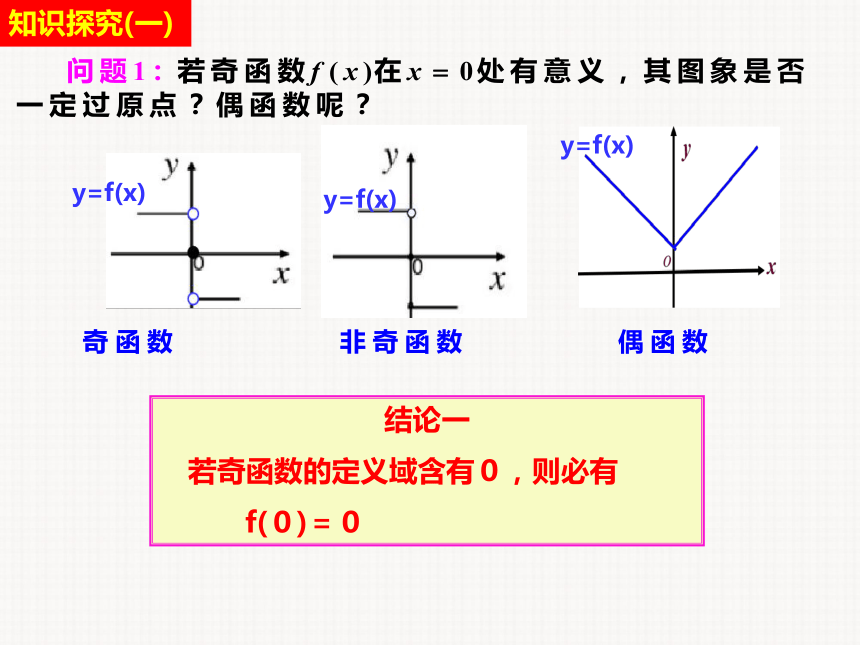
知识探究(一)
y=f(x)
y=f(x)
y=f(x)
结论一
若奇函数的定义域含有0,则必有
f(0)=0
又∵f(1)=3,
综上,a=3,b=0
解:
∴由f(-x)=-f(x)得
例析
例1.设函数 是奇函数,且f(1)=3,则求a,b.
∵函数f(x)是奇函数
思考(1):对于是函数f(x)奇函数这个条件还可以怎样用
由f(x)的定义域含0可知
f(0)=0
解得a=3
思考(1):若将“f(-x)=-f(x)”换为“f(-x)+f(x)=0”,对应的运算量如何
∴定义域关于原点对称①,
由②得,
∴ b=-2.
综上,a=-1,b=-2。
解: ∵函数f(x)是偶函数
已知函数f(x)=ax2+(b+2)x+3,x∈(2a+1,1)是偶函数,则求a,b.
且f(-x)-f(x=0)②
由①得
∴a=-1,
(2a+1)=-1
[-(-x)2-(b+2)x+3]-
[-x2+(b+2)x+3]=0
即2bx+4x= 0
练习
思考(1):“f(-x)=f(x)②”是否可以特殊化
∵函数的定义域为(-1,1)
f(x)=-x2+(b+2)x+3
∴ b=-2.
思考(2): 利用奇偶性求参数的值,一般可利用的条件哪一些
①定义域的对称性;②f(-x)=±f(x)恒成立;③在定义域内将f(-x)=±f(x)特殊化;④奇函数定义域含0时,f(0)=0.
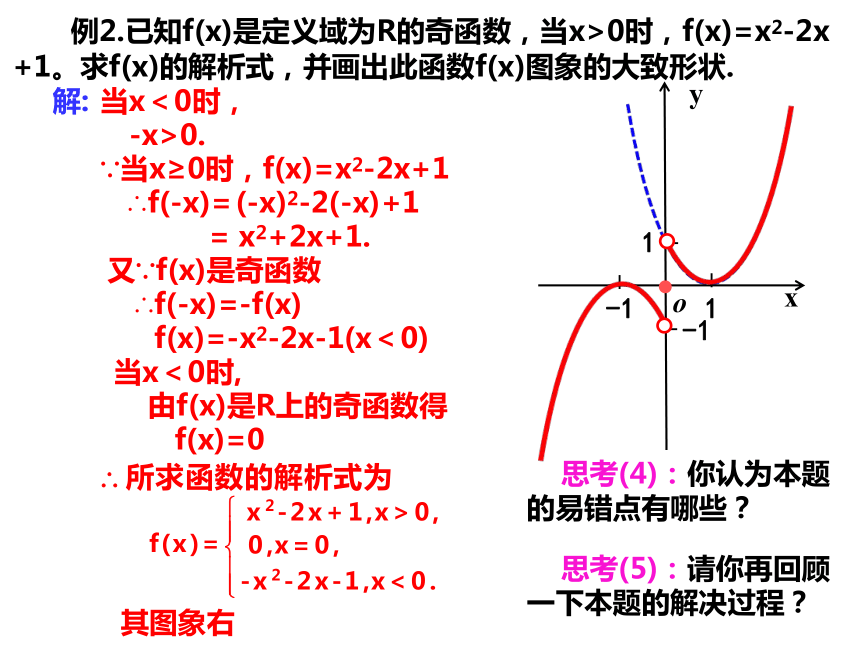
例2.已知f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x+1。求f(x)的解析式,并画出此函数f(x)图象的大致形状.
例析
思考(1):”当x>0时,f(x)=x2-2x+1”的言外之意是什么
当x<0或x=0时,f(x)=x2-2x+1就不一定成立了,即
函数f(x)是一个分段函数。
思考(2):因此,解决本题关键是什么?
求出”当x<0或x=0时f(x)的对应关系”。
当x=0时,f(x)=0
既然要求x<0时f(x)的对应关系,首先就取”x<0”,
但此时x无法代入f(x)=x2-2x+1(x≥0才成立),接下来作一个对称”-x>0”,
然后将-x代入f(x)=x2-2x+1得到f(-x),
最后利用f(-x)与f(x)的关系得到x<0时的f(x)。
思考(3):既然f(x)是定义域为R的奇函数,x=0时,f(x)等于多少?
思考(4):根据题目中的条件,你认为本题应如何入求当x<0时的对应关系?
例2.已知f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x+1。求f(x)的解析式,并画出此函数f(x)图象的大致形状.
又∵f(x)是奇函数
∴f(-x)=-f(x)
∵当x≥0时,f(x)=x2-2x+1
当x<0时,
∴f(-x)=
f(x)=-x2-2x-1
其图象右
(-x)2-2(-x)+1
(x<0)
= x2+2x+1.
解:
-x>0.
思考(4):你认为本题的易错点有哪些?
当x<0时,
f(x)=0
由f(x)是R上的奇函数得
x
y
o
-1
1
1
-1
思考(5):请你再回顾一下本题的解决过程?
例2.已知f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x+1。求f(x)的解析式,并画出此函数f(x)图象的大致形状.
利用奇偶性求分段函数解析式的一般过程:
(1)取范围: 将x取在需要求对应关系时的范围;
(2)调范围: 把含有x式子调整到已知对应关系时的范围;
(3)代入: 将调整后式子代入已知的解析式;
(4)求出f(x): 根据奇偶性求出该范围的解析式;
(5)作结论:写成分段函数的形式
已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-2x+1。
(1)求f(-3); (2)求f(x)的解析式,并画出函数f(x)图象的大致形状.
又∵f(x)是偶函数
∴f(-x)=f(x)=x2+2x+1.
∵当x≥0时,f(x)=x2-2x+1
设x<0,则
∴f(-x)=
即f(x)=x2+2x+1
其图象右
(-x)2-2(-x)+1
(x<0)
= x2+2x+1.
解:(1)
-x>0.
x
y
o
-1
1
1
练习
取范围
调范围
代入
求出f(x)
作结论
思考:本题和刚才的例题有何不同?为什么x=0不需单独考虑
∵f(x)是偶函数
∴f(-3)=f(3)
=32-2×3+1
=4
(2)
y=f(x)
问题2:已知偶函数y=f(x)在区间[a,b]单调递增,你能判断y=f(x)在[-b,-a]的单调性吗?
x1, x2∈[-b,-a],且x1∵f(x)在[a,b]单调递增
又∵f(x)在R上是奇函数
即 f(x1) < f(x2)
∴函数y=f(x)在区间[-b,-a]单调递减
知识探究(二)
a
b
函数y=f(x)在区间[-b,-a]单调递减
-x1, -x2∈[a,b],且-x1>-x2
∴由-x1, -x2∈[a,b],且-x1>-x2 得
f(-x1)>f(-x1)
∴f(-x1)=-f(x1)>f(-x2)=-f(x2)
证明:
-b
-a
-x2
-x1
x1
x2
思考:若y=f(x)是奇函数,情况又会怎样?
y=f(x)在[-b,-a]单调递增
结论二
在关于原点的两个对称区间上:
奇函数的单调性相同; 偶函数的单调性相反.
例3.已知函数f(x)是定义域为(-1,1)的奇函数 ,且在[0,1)上是增函数. 解不等式:
又∵奇函数f(x)在[0,1)上是增函数,
∵f(x)在R上是奇函数,
例析
∴f(x)是增函数。
解:
例3.已知函数f(x)是定义域为(-1,1)的奇函数 ,且在[0,1)上是增函数. 解不等式:
思考(1):若将”[0,1)”改为”(0,1)”,情况会怎样
不等式没法解,因为f(x)不一定还是增函数。
除非加上另加条件,如图象连续不断。
x
y
o
1
-1
x
y
o
1
-1
1.已知函数f(x)是奇函数,且在区间[3,7]上为单调递增,若f(x)在区间[3,7]上的最小值是5,最大值是6,求函数f(x)在区间[-7,-3]最大值。
简析:
由题意知
练习
2.若将上题的奇函数改为偶函数,函数f(x)在区间[-7,-3]最大值为__________.
-7
-3
-5
3
5
x
y
7
o
6
-6
函数f(x)在区间[-7,-3]上单调递增
∵f(x)是奇函数
∴f(x)在区间[-7,-3]上的最大值为
f(-3)
∴f(-3)=-f(3)
由题意知f(3)=5
∴f(-3)=-5
6
即函数f(x)在区间[-7,-3]最大值为-5
3.已知函数y=f(x)是R上的奇函数,g(x)=xf(x)在(0,+∞)上是减函数, 且f(2)=0 . 解不等式g(x)≥0 .
∵函数y=f(x)是R上的偶函数,
∴g(x)=xf(x)在R上是奇函数.
由图象可得不等式g(x)≥0的解集为:
解:
x
y
o
2
-2
(-∞,-2]∪
{0}∪
(0,2]=
(-∞,-2]∪
[0,2]
又∵g(2)=
2f(2)=0,
且g(x)在(0,+∞)上是减函数,
∴g(x)图象的大致形状为
知识探究(三)
结论三
练习
简析:
1. 奇函数的定义域含0时,其图象一定过原点吗?
小结
2.奇函数和偶函数在单调性上有什么性质?
5.通过本节的学习,你对“数形结合的思想方法”,“特殊与
一般”的思想方法有什么认识?
3.如何根据奇偶性求函数的解析式?
在运算上呢?
4.如何解与抽象函数有关的不等式?
作 业
1.教材P86习题3.2第11题
3.已知奇函数f(x)在[0,+∞)单调递减, 解不等式 :
4.(选做题)教材P86习题3.2第13题
简析:
3.已知奇函数f(x)在[0,+∞)单调递减, 解不等式 :
∵f(x)是奇函数
∵f(x)在[0,+∞)单调递减
∵f(x)在[0,+∞)单调递减
∴(x)在为减函数
3.2 函数的基本性质
3.2.2 奇偶性
第2课时
复习与回顾
1.什么是奇函数,偶函数?它们的特征各是怎样的?
(1)图象法(直观判断);
(2)定义法(严格推导)。
2.如何判定一个函数的奇偶性?
3.函数的单调性和奇偶性各反应了函数怎样的性质?
单调性反映的是函数的增减性,奇偶性反映的是函数的对称性;
单调性针对的是定义域下的某一个区间,奇偶性针对的是整个定义域。
新课
2.奇偶函数的特征:
对于奇函数有:f(-x)=-f(x)
一般地,设函数f(x)的定义域为Ⅰ,
如果 x∈Ⅰ,都有-x∈Ⅰ,且
f(-x)=-f(x)
那么函数f(x)就叫做奇函数(evenfunction).
如果 x∈Ⅰ,都有-x∈Ⅰ,且
f(-x)=f(x)
那么函数f(x)就叫做偶函数(evenfunction).
1. 定义
函数的奇偶性
奇函数图象关于原点对称;
(2)代数特征:
(3)几何特征:
(1)定义域特征:
定义域关于原点对称.
(自变量取一对相反数时,函数值也是一对相反数)
返回
(或f(-x)+f(x)=0)
(或f(-x)-f(x)=0)
对于偶函数有:f(-x)=f(x)
偶函数图象关于y轴对称.
(自变量取一对相反数时,函数值相等)
(1)求函数的定义域Ⅰ;
(2)判断定义域Ⅰ是否关于原点对称;
若定义域Ⅰ关于原点对称,则函数不具有奇偶性;
若定义域Ⅰ关于原点对称关于原点对称,则进入第三步.
(3) x∈Ⅰ,计算f(-x),并判断f(-x)与f(x)的关系;
(4)作结论.
若f(-x)=-f(x),则函数是奇函数;
若f(-x)=f(x),则函数是偶函数;
若f(-x)≠f(x)且f(-x)=-f(x) ,则f(x)既非奇函数又非偶函数;
若f(-x)=f(x)且f(-x)=-f(x) ,则f(x)既是奇函数又是偶函数.
用定义法判定函数f(x)的奇偶性的步骤
返回
一求二看
三算
四断
知识探究(一)
y=f(x)
y=f(x)
y=f(x)
结论一
若奇函数的定义域含有0,则必有
f(0)=0
又∵f(1)=3,
综上,a=3,b=0
解:
∴由f(-x)=-f(x)得
例析
例1.设函数 是奇函数,且f(1)=3,则求a,b.
∵函数f(x)是奇函数
思考(1):对于是函数f(x)奇函数这个条件还可以怎样用
由f(x)的定义域含0可知
f(0)=0
解得a=3
思考(1):若将“f(-x)=-f(x)”换为“f(-x)+f(x)=0”,对应的运算量如何
∴定义域关于原点对称①,
由②得,
∴ b=-2.
综上,a=-1,b=-2。
解: ∵函数f(x)是偶函数
已知函数f(x)=ax2+(b+2)x+3,x∈(2a+1,1)是偶函数,则求a,b.
且f(-x)-f(x=0)②
由①得
∴a=-1,
(2a+1)=-1
[-(-x)2-(b+2)x+3]-
[-x2+(b+2)x+3]=0
即2bx+4x= 0
练习
思考(1):“f(-x)=f(x)②”是否可以特殊化
∵函数的定义域为(-1,1)
f(x)=-x2+(b+2)x+3
∴ b=-2.
思考(2): 利用奇偶性求参数的值,一般可利用的条件哪一些
①定义域的对称性;②f(-x)=±f(x)恒成立;③在定义域内将f(-x)=±f(x)特殊化;④奇函数定义域含0时,f(0)=0.
例2.已知f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x+1。求f(x)的解析式,并画出此函数f(x)图象的大致形状.
例析
思考(1):”当x>0时,f(x)=x2-2x+1”的言外之意是什么
当x<0或x=0时,f(x)=x2-2x+1就不一定成立了,即
函数f(x)是一个分段函数。
思考(2):因此,解决本题关键是什么?
求出”当x<0或x=0时f(x)的对应关系”。
当x=0时,f(x)=0
既然要求x<0时f(x)的对应关系,首先就取”x<0”,
但此时x无法代入f(x)=x2-2x+1(x≥0才成立),接下来作一个对称”-x>0”,
然后将-x代入f(x)=x2-2x+1得到f(-x),
最后利用f(-x)与f(x)的关系得到x<0时的f(x)。
思考(3):既然f(x)是定义域为R的奇函数,x=0时,f(x)等于多少?
思考(4):根据题目中的条件,你认为本题应如何入求当x<0时的对应关系?
例2.已知f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x+1。求f(x)的解析式,并画出此函数f(x)图象的大致形状.
又∵f(x)是奇函数
∴f(-x)=-f(x)
∵当x≥0时,f(x)=x2-2x+1
当x<0时,
∴f(-x)=
f(x)=-x2-2x-1
其图象右
(-x)2-2(-x)+1
(x<0)
= x2+2x+1.
解:
-x>0.
思考(4):你认为本题的易错点有哪些?
当x<0时,
f(x)=0
由f(x)是R上的奇函数得
x
y
o
-1
1
1
-1
思考(5):请你再回顾一下本题的解决过程?
例2.已知f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x+1。求f(x)的解析式,并画出此函数f(x)图象的大致形状.
利用奇偶性求分段函数解析式的一般过程:
(1)取范围: 将x取在需要求对应关系时的范围;
(2)调范围: 把含有x式子调整到已知对应关系时的范围;
(3)代入: 将调整后式子代入已知的解析式;
(4)求出f(x): 根据奇偶性求出该范围的解析式;
(5)作结论:写成分段函数的形式
已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-2x+1。
(1)求f(-3); (2)求f(x)的解析式,并画出函数f(x)图象的大致形状.
又∵f(x)是偶函数
∴f(-x)=f(x)=x2+2x+1.
∵当x≥0时,f(x)=x2-2x+1
设x<0,则
∴f(-x)=
即f(x)=x2+2x+1
其图象右
(-x)2-2(-x)+1
(x<0)
= x2+2x+1.
解:(1)
-x>0.
x
y
o
-1
1
1
练习
取范围
调范围
代入
求出f(x)
作结论
思考:本题和刚才的例题有何不同?为什么x=0不需单独考虑
∵f(x)是偶函数
∴f(-3)=f(3)
=32-2×3+1
=4
(2)
y=f(x)
问题2:已知偶函数y=f(x)在区间[a,b]单调递增,你能判断y=f(x)在[-b,-a]的单调性吗?
x1, x2∈[-b,-a],且x1
又∵f(x)在R上是奇函数
即 f(x1) < f(x2)
∴函数y=f(x)在区间[-b,-a]单调递减
知识探究(二)
a
b
函数y=f(x)在区间[-b,-a]单调递减
-x1, -x2∈[a,b],且-x1>-x2
∴由-x1, -x2∈[a,b],且-x1>-x2 得
f(-x1)>f(-x1)
∴f(-x1)=-f(x1)>f(-x2)=-f(x2)
证明:
-b
-a
-x2
-x1
x1
x2
思考:若y=f(x)是奇函数,情况又会怎样?
y=f(x)在[-b,-a]单调递增
结论二
在关于原点的两个对称区间上:
奇函数的单调性相同; 偶函数的单调性相反.
例3.已知函数f(x)是定义域为(-1,1)的奇函数 ,且在[0,1)上是增函数. 解不等式:
又∵奇函数f(x)在[0,1)上是增函数,
∵f(x)在R上是奇函数,
例析
∴f(x)是增函数。
解:
例3.已知函数f(x)是定义域为(-1,1)的奇函数 ,且在[0,1)上是增函数. 解不等式:
思考(1):若将”[0,1)”改为”(0,1)”,情况会怎样
不等式没法解,因为f(x)不一定还是增函数。
除非加上另加条件,如图象连续不断。
x
y
o
1
-1
x
y
o
1
-1
1.已知函数f(x)是奇函数,且在区间[3,7]上为单调递增,若f(x)在区间[3,7]上的最小值是5,最大值是6,求函数f(x)在区间[-7,-3]最大值。
简析:
由题意知
练习
2.若将上题的奇函数改为偶函数,函数f(x)在区间[-7,-3]最大值为__________.
-7
-3
-5
3
5
x
y
7
o
6
-6
函数f(x)在区间[-7,-3]上单调递增
∵f(x)是奇函数
∴f(x)在区间[-7,-3]上的最大值为
f(-3)
∴f(-3)=-f(3)
由题意知f(3)=5
∴f(-3)=-5
6
即函数f(x)在区间[-7,-3]最大值为-5
3.已知函数y=f(x)是R上的奇函数,g(x)=xf(x)在(0,+∞)上是减函数, 且f(2)=0 . 解不等式g(x)≥0 .
∵函数y=f(x)是R上的偶函数,
∴g(x)=xf(x)在R上是奇函数.
由图象可得不等式g(x)≥0的解集为:
解:
x
y
o
2
-2
(-∞,-2]∪
{0}∪
(0,2]=
(-∞,-2]∪
[0,2]
又∵g(2)=
2f(2)=0,
且g(x)在(0,+∞)上是减函数,
∴g(x)图象的大致形状为
知识探究(三)
结论三
练习
简析:
1. 奇函数的定义域含0时,其图象一定过原点吗?
小结
2.奇函数和偶函数在单调性上有什么性质?
5.通过本节的学习,你对“数形结合的思想方法”,“特殊与
一般”的思想方法有什么认识?
3.如何根据奇偶性求函数的解析式?
在运算上呢?
4.如何解与抽象函数有关的不等式?
作 业
1.教材P86习题3.2第11题
3.已知奇函数f(x)在[0,+∞)单调递减, 解不等式 :
4.(选做题)教材P86习题3.2第13题
简析:
3.已知奇函数f(x)在[0,+∞)单调递减, 解不等式 :
∵f(x)是奇函数
∵f(x)在[0,+∞)单调递减
∵f(x)在[0,+∞)单调递减
∴(x)在为减函数
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
