《1.4分式的加法和减法》能力达标测评 2021-2022学年湘教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 《1.4分式的加法和减法》能力达标测评 2021-2022学年湘教版八年级数学上册(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 284.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 18:36:44 | ||
图片预览
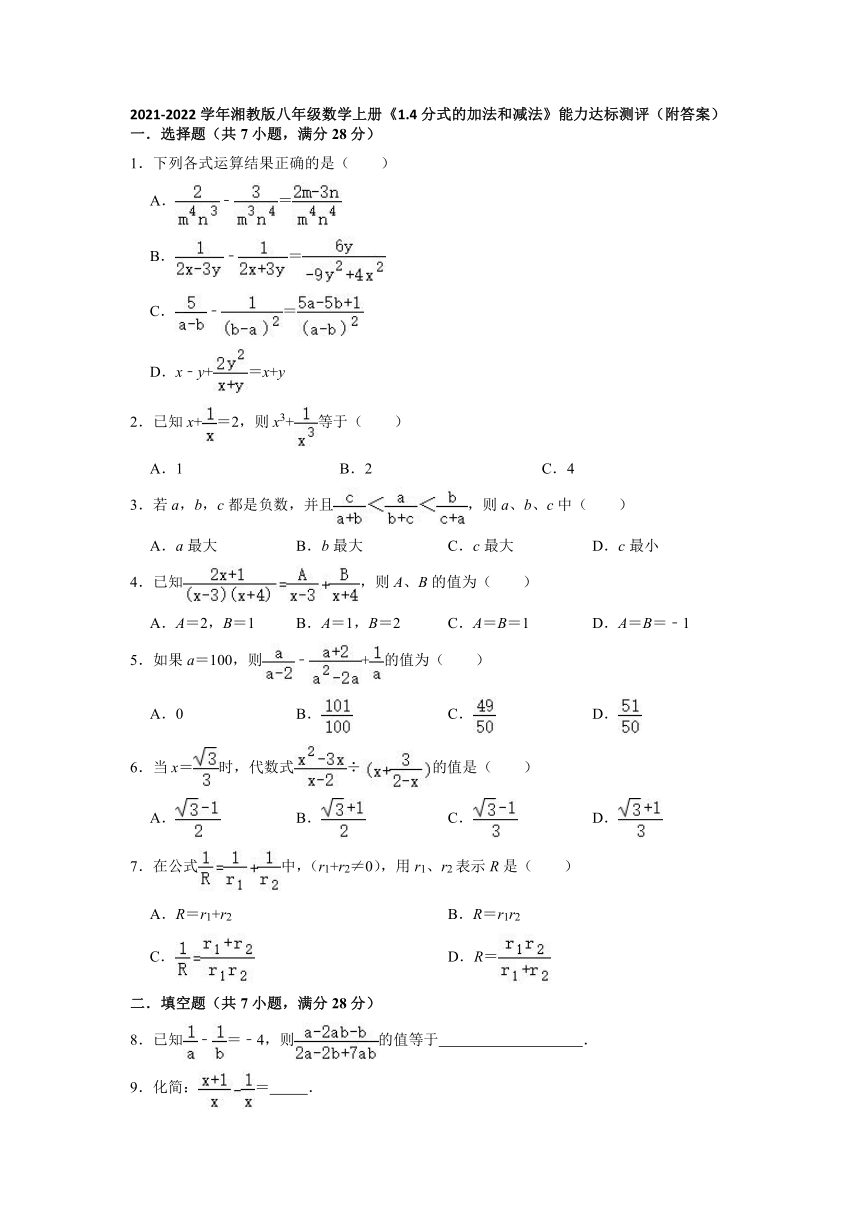




文档简介
2021-2022学年湘教版八年级数学上册《1.4分式的加法和减法》能力达标测评(附答案)
一.选择题(共7小题,满分28分)
1.下列各式运算结果正确的是( )
A.﹣=
B.﹣=
C.﹣=
D.x﹣y+=x+y
2.已知x+=2,则x3+等于( )
A.1 B.2 C.4
3.若a,b,c都是负数,并且,则a、b、c中( )
A.a最大 B.b最大 C.c最大 D.c最小
4.已知,则A、B的值为( )
A.A=2,B=1 B.A=1,B=2 C.A=B=1 D.A=B=﹣1
5.如果a=100,则﹣+的值为( )
A.0 B. C. D.
6.当x=时,代数式÷的值是( )
A. B. C. D.
7.在公式中,(r1+r2≠0),用r1、r2表示R是( )
A.R=r1+r2 B.R=r1r2
C. D.R=
二.填空题(共7小题,满分28分)
8.已知﹣=﹣4,则的值等于 .
9.化简:= .
10.已知ab=2,a2+b2=4,则式子+= .
11.计算:++= .
12.计算(a﹣)÷的结果是 .
13.计算:= .
14.a,b互为相反数,且|a﹣b|=4,那么= .
三.解答题(共10小题,满分64分)
15.先化简,再求值:(a﹣9+)÷(a﹣1﹣),其中a=.
16.先化简,再求值:(﹣)÷(﹣) (++2),其中+(n﹣3)2=0.
17.先化简,再求值:,其中x=.
18.先化简:然后解答下列问题:
(1)当x=2时,求代数式的值
(2)原代数式的值能等于0吗?为什么?
19.先化简,再求值:(﹣m﹣3)÷,其中m=4﹣
20.先化简,再求值:,其中x是从0,1,3,5中选取的一个合适的数.
21.先化简 (1+)÷,然后在0,1,﹣1中挑选一个合适的数代入求值.
22.已知a+b+c=0,求的值.
23.在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律,由“特殊”到“一般”进行抽象概括的:22×23=25,23×24=27,22×26=28,… 2m×2n=2m+n,… am×an=am+n(m、n都是正整数).
探索问题:
(1)比较下列各组数据的大小:
① ,② ,③ ,④ ,….
(2)请你根据上面的材料归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式;并用已学的数学知识说明你发现结论的正确性.
(3)试用(2)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”.
24.“丰收1号“小麦的试验田是边长为am(a>1)的正方形去掉一个边长为1m的正方蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a﹣1)m的正方形,两块试验田的小麦都收获了500kg,试说明哪种小麦的单位面积产量高.
参考答案
一.选择题(共7小题,满分28分)
1.解:∵=,故选项A错误,
∵=,故选项B正确,
∵=,故选项C错误,
∵=,故选项D错误,
故选:B.
2.解:∵x+=2,
∴=4,
∴=2,
∴x3+=(x+)(+)=2×(2﹣1)=2.
故选:B.
3.解:∵,
∴,
∴<<,又a、b、c都是负数,
∴a+b<b+c<c+a,
∴b<a<c,
故选:C.
4.解:∵===,
∴,
解得:.
故选:C.
5.解:原式=﹣+
=﹣+
=
=
=,
当a=100时,原式==.
故选:D.
6.解:原式=÷(﹣)
=÷
=×
=,
当x=时,原式==.
故选:A.
7.解:两边同乘以最简公分母Rr1r2,得
r1r2=(r1+r2)R
两边同除以r1+r2,得R=.故选D.
二.填空题(共7小题,满分28分)
8.解:∵﹣=﹣4,
∴=﹣4,
∴b﹣a=﹣4ab,
∴a﹣b=4ab,
原式=
=
=
=.
故答案为.
9.解:===1.
故答案为:1.
10.解:+=+=,
把ab=2,a2+b2=4代入可得:原式==2.
故答案为:2.
11.解:原式==,
故答案为:
12.解:原式= = =a﹣b,
故答案为:a﹣b
13.解:===﹣2.
故答案为﹣2.
14.解:当a>0且b=﹣a,时,则2a=4,a=2,b=﹣2,则=7;
当a<0且b=﹣a,时,则2a=﹣4,a=﹣2,b=2,原式=(﹣2+4+1)÷(4﹣4+1)=3.
三.解答题(共10小题,满分64分)
15.解:原式=(+)÷(﹣)
=÷
=
=,
当a=时,
原式==1﹣2.
16.解:(﹣)÷(﹣) (++2)
=÷
=
=﹣.
∵+(n﹣3)2=0.
∴m+1=0,n﹣3=0,
∴m=﹣1,n=3.
∴﹣=﹣=.
∴原式的值为.
17.解:
=
=
=,
当x=时,原式=.
18.解:
=[]
=() (x+1)
=
=,
(1)当x=2时,原式==3;
(2)原代数式的值不等等于0,
理由:令=0,得x=﹣1,
当x=﹣1时,原分式无意义,
故原代数式的值不能等于0.
19.解:原式=(﹣)÷
=÷
=
=﹣
=,
当m=4﹣时,
原式===
20.解:原式=(﹣)÷
=
=,
当x=3时,原式==﹣.
21.解:原式=
=x﹣1.
∵x≠0,1,
∴当x=﹣1时,原式=﹣2.
22.解:
=
=
∵a+b+c=0,则a+b=﹣c,a+c=﹣b,b+c=﹣a,
∴原式==﹣3.
故答案为﹣3.
23.解:(1)比较下列各组数据的大小:
∵=,=,=,=,
∴①<,②<,③<,④<;
(2)你根据上面的材料可得:<.
说明:∵﹣=﹣===,
又∵a>b>0,c>0,
∴a+c>0,b﹣a<0,
∴<0,
∴﹣<0,
即:<成立;
(3)∵原来糖水中糖的质量分数=,
加入k克糖后糖水中糖的质量分数+,
由(2)<可得<,
所以糖水更甜了.
24.解:“丰收1号”小麦的试验田面积是(a2﹣1)m2,单位面积产量是kg/m2;“丰收2号”小麦的试验田面积是(a﹣1)2m2,单位面积产量是kg/m2,
∵a>1,即a﹣1>0,
∴(a﹣1)2﹣(a2﹣1)=a2﹣2a+1﹣a2+1=﹣2a+2=﹣2(a﹣1)<0,
∴(a﹣1)2<(a2﹣1),
又由a>1可得(a﹣1)2>0,a2﹣1>0,
∴<,
则“丰收2号”小麦的单位面积产量高.
一.选择题(共7小题,满分28分)
1.下列各式运算结果正确的是( )
A.﹣=
B.﹣=
C.﹣=
D.x﹣y+=x+y
2.已知x+=2,则x3+等于( )
A.1 B.2 C.4
3.若a,b,c都是负数,并且,则a、b、c中( )
A.a最大 B.b最大 C.c最大 D.c最小
4.已知,则A、B的值为( )
A.A=2,B=1 B.A=1,B=2 C.A=B=1 D.A=B=﹣1
5.如果a=100,则﹣+的值为( )
A.0 B. C. D.
6.当x=时,代数式÷的值是( )
A. B. C. D.
7.在公式中,(r1+r2≠0),用r1、r2表示R是( )
A.R=r1+r2 B.R=r1r2
C. D.R=
二.填空题(共7小题,满分28分)
8.已知﹣=﹣4,则的值等于 .
9.化简:= .
10.已知ab=2,a2+b2=4,则式子+= .
11.计算:++= .
12.计算(a﹣)÷的结果是 .
13.计算:= .
14.a,b互为相反数,且|a﹣b|=4,那么= .
三.解答题(共10小题,满分64分)
15.先化简,再求值:(a﹣9+)÷(a﹣1﹣),其中a=.
16.先化简,再求值:(﹣)÷(﹣) (++2),其中+(n﹣3)2=0.
17.先化简,再求值:,其中x=.
18.先化简:然后解答下列问题:
(1)当x=2时,求代数式的值
(2)原代数式的值能等于0吗?为什么?
19.先化简,再求值:(﹣m﹣3)÷,其中m=4﹣
20.先化简,再求值:,其中x是从0,1,3,5中选取的一个合适的数.
21.先化简 (1+)÷,然后在0,1,﹣1中挑选一个合适的数代入求值.
22.已知a+b+c=0,求的值.
23.在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律,由“特殊”到“一般”进行抽象概括的:22×23=25,23×24=27,22×26=28,… 2m×2n=2m+n,… am×an=am+n(m、n都是正整数).
探索问题:
(1)比较下列各组数据的大小:
① ,② ,③ ,④ ,….
(2)请你根据上面的材料归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式;并用已学的数学知识说明你发现结论的正确性.
(3)试用(2)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”.
24.“丰收1号“小麦的试验田是边长为am(a>1)的正方形去掉一个边长为1m的正方蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a﹣1)m的正方形,两块试验田的小麦都收获了500kg,试说明哪种小麦的单位面积产量高.
参考答案
一.选择题(共7小题,满分28分)
1.解:∵=,故选项A错误,
∵=,故选项B正确,
∵=,故选项C错误,
∵=,故选项D错误,
故选:B.
2.解:∵x+=2,
∴=4,
∴=2,
∴x3+=(x+)(+)=2×(2﹣1)=2.
故选:B.
3.解:∵,
∴,
∴<<,又a、b、c都是负数,
∴a+b<b+c<c+a,
∴b<a<c,
故选:C.
4.解:∵===,
∴,
解得:.
故选:C.
5.解:原式=﹣+
=﹣+
=
=
=,
当a=100时,原式==.
故选:D.
6.解:原式=÷(﹣)
=÷
=×
=,
当x=时,原式==.
故选:A.
7.解:两边同乘以最简公分母Rr1r2,得
r1r2=(r1+r2)R
两边同除以r1+r2,得R=.故选D.
二.填空题(共7小题,满分28分)
8.解:∵﹣=﹣4,
∴=﹣4,
∴b﹣a=﹣4ab,
∴a﹣b=4ab,
原式=
=
=
=.
故答案为.
9.解:===1.
故答案为:1.
10.解:+=+=,
把ab=2,a2+b2=4代入可得:原式==2.
故答案为:2.
11.解:原式==,
故答案为:
12.解:原式= = =a﹣b,
故答案为:a﹣b
13.解:===﹣2.
故答案为﹣2.
14.解:当a>0且b=﹣a,时,则2a=4,a=2,b=﹣2,则=7;
当a<0且b=﹣a,时,则2a=﹣4,a=﹣2,b=2,原式=(﹣2+4+1)÷(4﹣4+1)=3.
三.解答题(共10小题,满分64分)
15.解:原式=(+)÷(﹣)
=÷
=
=,
当a=时,
原式==1﹣2.
16.解:(﹣)÷(﹣) (++2)
=÷
=
=﹣.
∵+(n﹣3)2=0.
∴m+1=0,n﹣3=0,
∴m=﹣1,n=3.
∴﹣=﹣=.
∴原式的值为.
17.解:
=
=
=,
当x=时,原式=.
18.解:
=[]
=() (x+1)
=
=,
(1)当x=2时,原式==3;
(2)原代数式的值不等等于0,
理由:令=0,得x=﹣1,
当x=﹣1时,原分式无意义,
故原代数式的值不能等于0.
19.解:原式=(﹣)÷
=÷
=
=﹣
=,
当m=4﹣时,
原式===
20.解:原式=(﹣)÷
=
=,
当x=3时,原式==﹣.
21.解:原式=
=x﹣1.
∵x≠0,1,
∴当x=﹣1时,原式=﹣2.
22.解:
=
=
∵a+b+c=0,则a+b=﹣c,a+c=﹣b,b+c=﹣a,
∴原式==﹣3.
故答案为﹣3.
23.解:(1)比较下列各组数据的大小:
∵=,=,=,=,
∴①<,②<,③<,④<;
(2)你根据上面的材料可得:<.
说明:∵﹣=﹣===,
又∵a>b>0,c>0,
∴a+c>0,b﹣a<0,
∴<0,
∴﹣<0,
即:<成立;
(3)∵原来糖水中糖的质量分数=,
加入k克糖后糖水中糖的质量分数+,
由(2)<可得<,
所以糖水更甜了.
24.解:“丰收1号”小麦的试验田面积是(a2﹣1)m2,单位面积产量是kg/m2;“丰收2号”小麦的试验田面积是(a﹣1)2m2,单位面积产量是kg/m2,
∵a>1,即a﹣1>0,
∴(a﹣1)2﹣(a2﹣1)=a2﹣2a+1﹣a2+1=﹣2a+2=﹣2(a﹣1)<0,
∴(a﹣1)2<(a2﹣1),
又由a>1可得(a﹣1)2>0,a2﹣1>0,
∴<,
则“丰收2号”小麦的单位面积产量高.
同课章节目录
