《2.3等腰三角形》知识点分类能力提升 2021-2022学年湘教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 《2.3等腰三角形》知识点分类能力提升 2021-2022学年湘教版八年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 377.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 18:37:34 | ||
图片预览


文档简介
2021-2022学年湘教版八年级数学上册《2.3等腰三角形》知识点分类能力提升(附答案)
一.等腰三角形的性质
1.如图,在△ABC中,AB=AC,∠A═55°,点P是AB上的一个动点,则∠APC的度数可能是( )
A.55° B.62° C.80° D.130°
2.等腰△ABC中,∠C=50°,则∠A的度数不可能是( )
A.80° B.50° C.65° D.45°
3.如果等腰三角形的一个角是80°,那么它的底角是( )
A.80°或50° B.50°或20° C.80°或20° D.50°
4.如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点,若∠CAE=16°,则∠B的大小为( )
A.32° B.36° C.37° D.74°
5.等腰三角形一腰上的高与另一腰的夹角为30°,则底角的度数为( )
A.60° B.120° C.60°或120° D.60°或30°
6.已知等腰三角形的两条边长分别是3cm、7cm,那么这个等腰三角形的周长是 cm.
7.已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为 .
8.等腰△ABC的腰AB边上的中线CD,把△ABC的周长分成12和15两部分,则底边BC长为 .
9.规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k,若k=,则该等腰三角形的底角为 .
10.如果等腰三角形有两条边长分别为2cm和3cm,那么它的周长是 .
11.已知等腰三角形的一个内角是50°,则等腰三角形的顶角等于 °.
12.等腰三角形一腰上的高与另一边的夹角为50°,则顶角的度数为 .
13.已知△ABC是等腰三角形.
(1)若∠A=100°,求∠B的度数;
(2)若∠A=70°,求∠B的度数;
(3)若∠A=α(45°<α<90°),过顶点B的角平分线BD与过顶点C的高CE交于点F,求∠BFC的度数(用含α的式子表示).
二.等腰三角形的判定
14.如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
15.已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.
A.3 B.4 C.5 D.6
16.如图是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是( )
A.4 B.5 C.6 D.7
17.如图,在Rt△ABC中,∠ACB=90°,∠CAB=36°,以C为原点,AC所在直线为y轴,BC所在直线为x轴建立平面直角坐标系,在坐标轴上取一点M使△MAB为等腰三角形,符合条件的M点有( )
A.6个 B.7个 C.8个 D.9个
18.如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
A.8个 B.7个 C.6个 D.5个
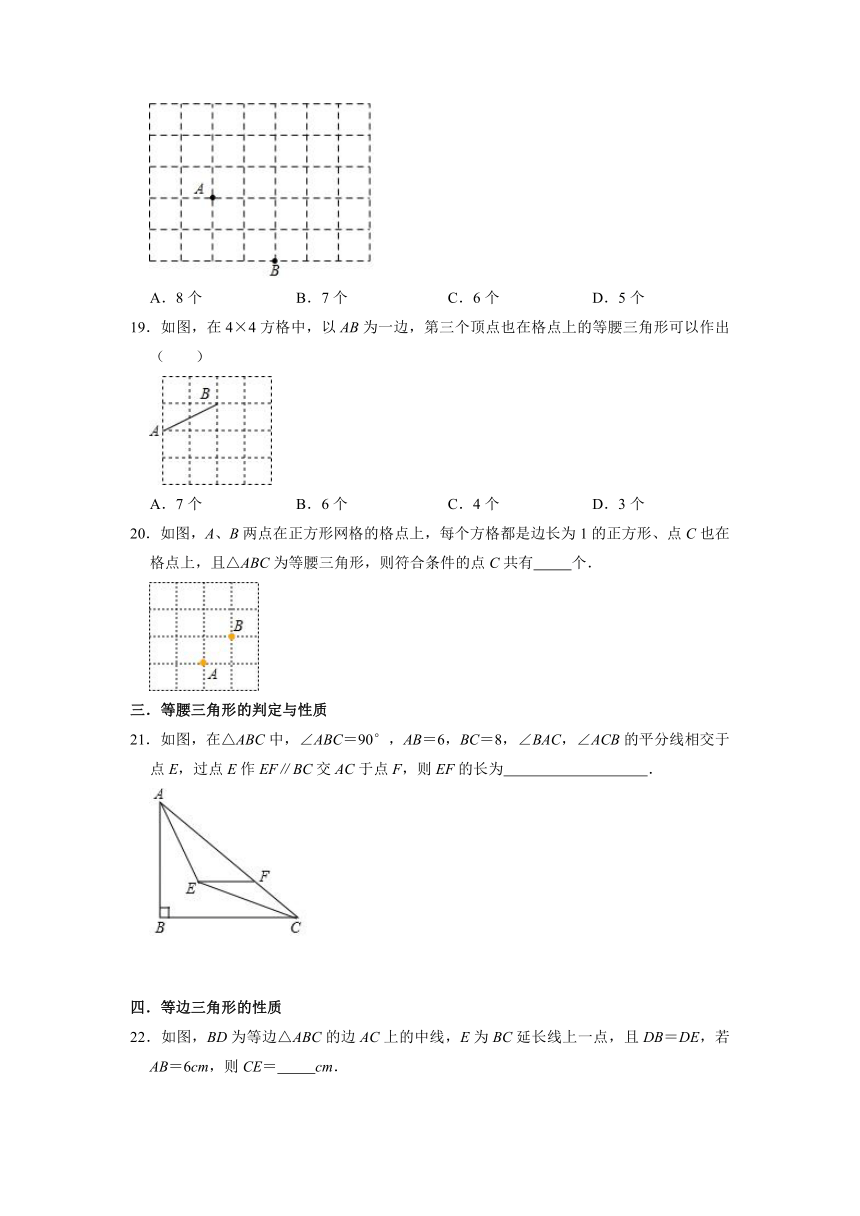
19.如图,在4×4方格中,以AB为一边,第三个顶点也在格点上的等腰三角形可以作出( )
A.7个 B.6个 C.4个 D.3个
20.如图,A、B两点在正方形网格的格点上,每个方格都是边长为1的正方形、点C也在格点上,且△ABC为等腰三角形,则符合条件的点C共有 个.
三.等腰三角形的判定与性质
21.如图,在△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为 .
四.等边三角形的性质
22.如图,BD为等边△ABC的边AC上的中线,E为BC延长线上一点,且DB=DE,若AB=6cm,则CE= cm.
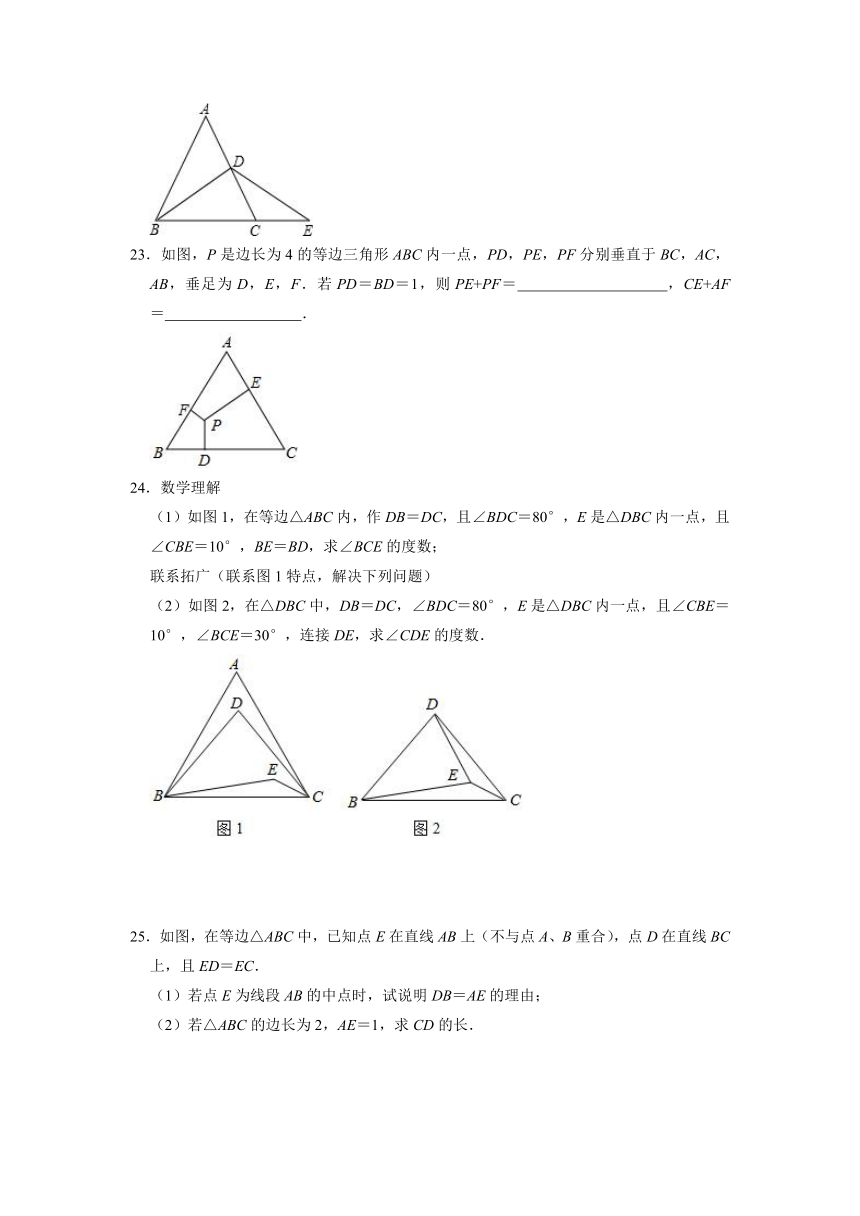
23.如图,P是边长为4的等边三角形ABC内一点,PD,PE,PF分别垂直于BC,AC,AB,垂足为D,E,F.若PD=BD=1,则PE+PF= ,CE+AF= .
24.数学理解
(1)如图1,在等边△ABC内,作DB=DC,且∠BDC=80°,E是△DBC内一点,且∠CBE=10°,BE=BD,求∠BCE的度数;
联系拓广(联系图1特点,解决下列问题)
(2)如图2,在△DBC中,DB=DC,∠BDC=80°,E是△DBC内一点,且∠CBE=10°,∠BCE=30°,连接DE,求∠CDE的度数.
25.如图,在等边△ABC中,已知点E在直线AB上(不与点A、B重合),点D在直线BC上,且ED=EC.
(1)若点E为线段AB的中点时,试说明DB=AE的理由;
(2)若△ABC的边长为2,AE=1,求CD的长.
五.等边三角形的判定
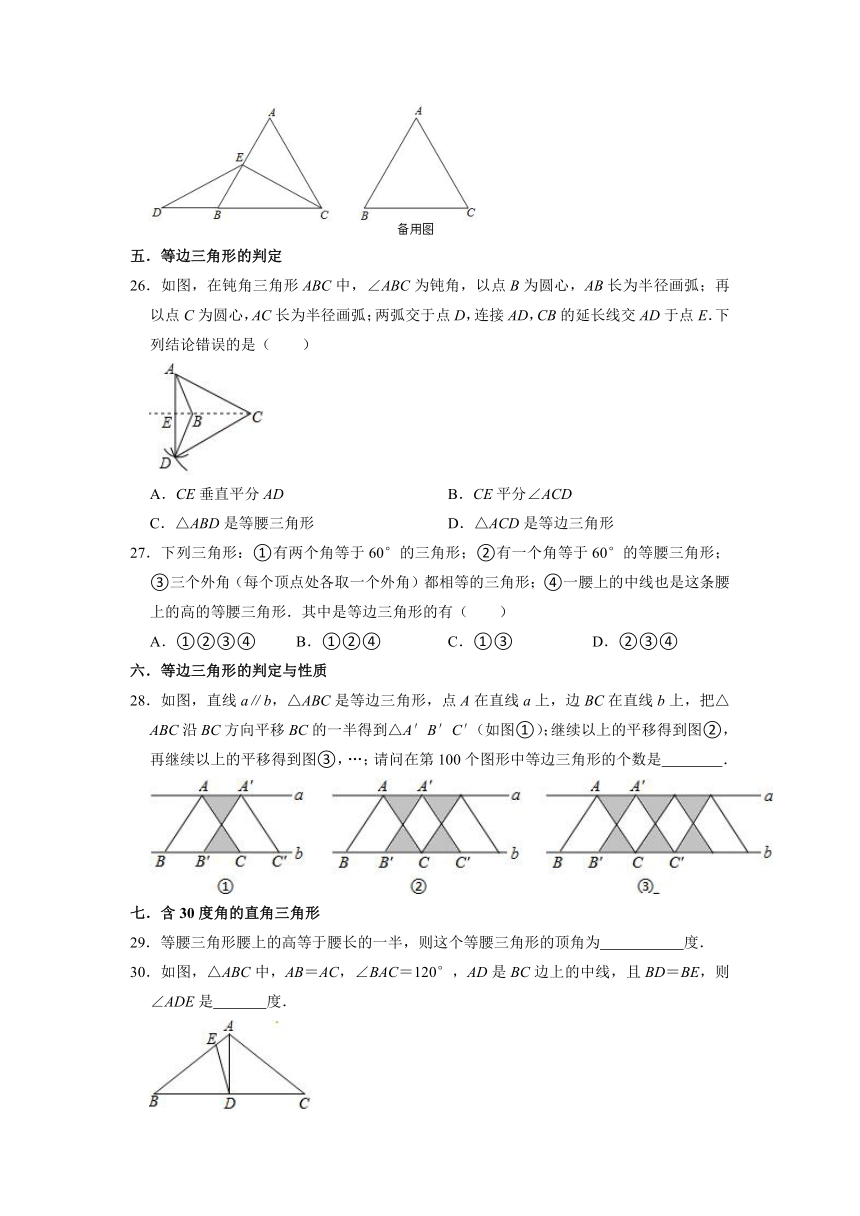
26.如图,在钝角三角形ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧;再以点C为圆心,AC长为半径画弧;两弧交于点D,连接AD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD B.CE平分∠ACD
C.△ABD是等腰三角形 D.△ACD是等边三角形
27.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③④ B.①②④ C.①③ D.②③④
六.等边三角形的判定与性质
28.如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是 .
七.含30度角的直角三角形
29.等腰三角形腰上的高等于腰长的一半,则这个等腰三角形的顶角为 度.
30.如图,△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,且BD=BE,则∠ADE是 度.
31.如图,在△ABC中,∠C=90°,∠A=30°,AB=4cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
(1)当t为何值时,△PBQ为等边三角形?
(2)当t为何值时,△PBQ为直角三角形?
参考答案
一.等腰三角形的性质
1.解:∵AB=AC,∠A═55°,
∴∠B=∠ACB=62.5°,
∵∠APC是△BCP的外角,
∴∠APC=∠B+∠BCP,
又∵点P是AB上的一个动点,
∴0≤∠BCP≤62.5°,
∴62.5°≤∠APC≤125°,
∴∠APC的度数可能是80°,
故选:C.
2.解:当∠C为顶角时,则∠A=(180°﹣50°)=65°;
当∠A为顶角时,则∠A=180°﹣2∠C=80°;
当∠A、∠C为底角时,则∠C=∠A=50°;
∴∠A的度数不可能是45°,
故选:D.
3.解:根据题意,一个等腰三角形的一个角等于80°,
①当这个角是底角时,即该等腰三角形的底角的度数是80°,
②当这个角80°是顶角,
设等腰三角形的底角是x°,
则2x+80°=180°,
解可得,x=50°,
即该等腰三角形的底角的度数是50°;
故选:A.
4.解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴∠C=90°﹣∠CAE=74°,
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故选:C.
5.解:如图,分两种情况:
①在左图中,AB=AC,BD⊥AC,∠ABD=30°,
∴∠A=60°,
∴∠C=∠ABC==60°;
②在右图中,AB=AC,BD⊥AC,∠ABD=30°,
∴∠DAB=60°,∠BAC=120°,
∴∠C=∠ABC==30°.
故选:D.
6.解:∵等腰三角形的两条边长分别是3cm、7cm,
∴当此三角形的腰长为3cm时,3+3<7,不能构成三角形,故排除,
∴此三角形的腰长为7cm,底边长为3cm,
∴此等腰三角形的周长=7+7+3=17cm,
故答案为:17.
7.解:△ABC,AB=AC.
有两种情况:
(1)顶角∠A=40°,
(2)当底角是40°时,
∵AB=AC,
∴∠B=∠C=40°,
∵∠A+∠B+∠C=180°,
∴∠A=180°﹣40°﹣40°=100°,
∴这个等腰三角形的顶角为40°和100°.
故答案为:40°或100°.
8.解:如图,在△ABC中,AB=AC,且AD=BD.设AB=x,BC=y,
①当AC+AD=15,BD+BC=12时,则x+x=15,x+y=12,
解得x=10,y=7.
②当AC+AD=12,BC+BD=15时,则x+x=12,x+y=15,
解得x=8,y=11,
综上所述,这个三角形的底边BC的长为7或11.
故答案为:7或11.
9.解:∵△ABC中,AB=AC,
∴∠B=∠C,
∵该等腰三角形的顶角与一个底角度数的比值为1:4,
∴∠A:∠B=1:4,
∵∠A+∠B+∠C=180°,
∴∠A+4∠A+4∠A=180°,
即9∠A=180°,
∴∠A=20°,∠B=80°,
故答案为:80°.
10.解:当2是腰时,2,2,3能组成三角形,
周长=3+2+2=7(cm);
当3是腰时,3,3,2能够组成三角形,
周长=3+3+2=8(cm),
综上所述,周长为7cm或8cm,
故答案为:7cm或8cm.
11.解:如图所示,△ABC中,设AB=AC.
分两种情况:
①顶角∠A=50°;
②当底角是50°时,
∵AB=AC,
∴∠B=∠C=50°,
∵∠A+∠B+∠C=180°,
∴∠A=180°﹣50°﹣50°=80°,
综上所述,这个等腰三角形的顶角为50°或80°.
故答案为:50或80.
12.解:△ABC是等腰三角形,且∠BAC为顶角,CD是腰AB的高.
(1)当等腰三角形是锐角三角形时,如图①;
∵∠ACD=50°,
∴∠BAC=90°﹣∠ACD=40°;
(2)当等腰三角形是钝角三角形时;
一、如图②﹣1;
当∠BCD=50°时,∠B=40°;
∴∠BAC=180°﹣2∠B=100°;
二、如图②﹣2;
当∠ACD=50°时,∠CAD=40°;
∴∠BAC=180°﹣∠CAD=140°;
故这个等腰三角形顶角的度数为:100°或140°或40°.
故答案为:100°或140°或40°.
13.解:(1)∵∠A=100°是钝角,
∴∠B=(180°﹣100°)=40°.
故∠B的度数为40°;
(2)若∠A为顶角,则∠B=(180°﹣∠A)÷2=55°;
若∠A为底角,∠B为顶角,则∠B=180°﹣2×70°=40°;
若∠A为底角,∠B为底角,则∠B=70°;
故∠B=55°或40°或70°;
(3)∵∠A=α(45°<α<90°),
①当∠A为顶角时,如图:
∵AB=AC,
∴∠ABC=∠ACB=(180°﹣α),
∵BD平分∠ABC,
∴∠ABD=∠CBD=ABC=(180°﹣α),
∴∠BFC=∠FEB+∠FBE=90°+(180°﹣α)=135°﹣α;
②当∠A为底角,∠B为底角时,如图:
∴∠BFC=∠FEB+∠FBE=90°+;
所以当∠A为底角时,最小值假设取45度,另一个底角也是45度,此时三角形ABC是直角三角形,
但是∠A 大于45°,所以两个底角的和一定大于90度,所以三角形ABC不可能是钝角三角形,
所以此种情况不存在.
当∠A为底角,∠B为底角时,∠C为顶角且为锐角时,如图:
∴∠BFC=∠FEB+∠FBE=90°+;
③当∠A为底角,∠B为顶角时,如图:
∵∠BFC+∠FBE=90°,
∠A+∠ABD=90°,
∵∠FBE=∠ABD,
∴∠BFC=∠A=α.
∵∠A 大于45°,所以等腰三角形ABC一定是锐角三角形,
∴此种情况不符合题意;
当A为底角,三角形是锐角三角形时,
如图,
∵AB=BC,BD平分∠ABC,
∴BD⊥AC,
∴∠ADF=90°,
∵CE⊥AB,
∴∠AEF=90°,
根据四边形内角和定理,得
∴∠BFC=180﹣a.
故∠BFC的度数为:135°﹣α;90°+;180°﹣α.
二.等腰三角形的判定
14.解:①AB为等腰△ABC底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
15.解:如图所示:
当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形(AD,AE,AF,AG分别为分割线).
故选:B.
16.解:如图所示:
C在C1,C2,C3,C4位置上时,AC=BC;
C在C5,C6位置上时,AB=BC;
即满足点C的个数是6,
故选:C.
17.解:如图,
①以A为圆心,AB为半径画圆,交直线AC有二点M1,M2,交BC有一点M3,(此时AB=AM);
②以B为圆心,BA为半径画圆,交直线BC有二点M5,M4,交AC有一点M6(此时BM=BA).
③AB的垂直平分线交AC一点M7(MA=MB),交直线BC于点M8;
∴符合条件的点有8个.
故选:C.
18.解:当AB为底时,作AB的垂直平分线,可找出格点C的个数有5个,
当AB为腰时,分别以A、B点为顶点,以AB为半径作弧,可找出格点C的个数有3个;
∴这样的顶点C有8个.
故选:A.
19.解:如图所示,分别以A、B为圆心,AB长为半径画弧,则圆弧经过的格点C1、C2、C3、C4、C5、C6、C7即为第三个顶点的位置;作线段AB的垂直平分线,垂直平分线未经过网格中的格点.
故以AB为一边,第三个顶点也在格点上的等腰三角形可以作出7个.
故选:A.
20.解:①点C以点A为标准,AB为底边,符合点C的有5个;
②点C以点B为标准,AB为等腰三角形的一条边,符合点C的有4个.
所以符合条件的点C共有9个.
三.等腰三角形的判定与性质
21.解:过E作EG∥AB,交AC于G,则∠BAE=∠AEG,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴∠CAE=∠AEG,
∴AG=EG,
同理可得,EF=CF,
∵AB∥GE,BC∥EF,
∴∠BAC=∠EGF,∠BCA=∠EFG,
∵∠ABC=90°,AB=6,BC=8,
∴AC=10,
∴EG:EF:GF=AB:BC:AC=3:4:5,
设EG=3k=AG,则EF=4k=CF,FG=5k,
∵AC=10,
∴3k+5k+4k=10,
∴k=,
∴EF=4k=.
故答案为:.
四.等边三角形的性质
22.解:∵BD为等边△ABC的边AC上的中线,∴BD⊥AC,
∵DB=DE,∴∠DBC=∠E=30°
∵∠ACB=∠E+∠CDE=60°
∴∠CDE=30°
∴∠CDE=∠E,
即CE=CD=AC=3cm.
故填3.
23.解:过A作AG⊥BC于G,
∵△ABC是等边三角形,
∴CG=BC=2,
∴AG=2,
连接PA、PB、PC,
∵PD,PE,PF分别垂直于BC,AC,AB,
∴S△ABC=S△APB+S△PBC+S△APC,
+,
AB=AB(PE+1+PF),
∴PE+PF=2﹣1,
延长DP交AB于H,
∵PF⊥AB,PD⊥BC,
∴∠BFP=∠BDP=90°,
∵∠ABC=60°,
∴∠HFP=60°,
∴∠BHD=30°,
∵BD=1,
∴BH=2,DH=,
∵PD=1,
∴PH=﹣1,
Rt△PFH中,PF=,
∴FH==,
∴BF=BH﹣FH=2﹣=,
∴AF=4﹣BF=,
∵PE+PF=2﹣1,
∴PE=2﹣1﹣=,
Rt△PDC中,PC===,
∴CE====,
∴CE+AF==5
故答案为:2﹣1,5
24.解:(1)如图1,连接AD,
∵AB=AC,DB=DC,
∴直线AD是线段BC的垂直平分线,
∴AD平分∠BAC,
∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∴∠BAD=30°,
∵∠BDC=80°,
∴∠DBC=50°,
∴∠ABD=60°﹣50°=10°=∠CBE,
又∵AB=BC,BE=BD,
∴△ABD≌△CBE(SAS),
∴∠BCE=∠BAD=30°;
(2)如图2,作等边三角形ABC,连接AD,
由(1)解答知,∠BAD=∠BCE=30°,∠ABD=∠CBE=10°,
∴△ABD≌△CBE(SAS),
∴BD=BE,
∵∠DBE=60°﹣10°﹣10°=40°,
∴∠BDE=70°,
∴∠CDE=∠BDC﹣∠BDE=80°﹣70°=10°.
25.解:(1)∵△ABC是等边三角形,E为AB的中点,
∴∠BCE=30°,BE=AE,
∵ED=EC,
∴∠EDB=∠BCE=30°,
∵∠ABD=120°,
∴∠DEB=30°,
∴DB=EB,
∴AE=DB;
(2)如图1,E在线段AB上时,
∵AB=2,AE=1,
∴点E是AB的中点,
由(1)知,BD=AE=1,
∴CD=BC+BD=3;
如图2,E在线段AB的反向延长线上时,
∵AE=1,AB=2,
∴BE=3,
∵△ABC是等边三角形,
∴∠BAC=∠BCA=60°,AB=BC=AC=2,
过E作EH∥AC交BC的延长线于H,
∴∠BEH=∠BHE=60°,
∴△BEH是等边三角形,
∴BE=EH=BH=3,∠B=∠H=60°,
∵ED=EC,
∴∠EDC=∠ECD,
∴∠B+∠BED=∠H+∠HEC,
∴∠BED=∠HEC,
在△BDE和△HCE中,
,
∴△BDE≌△HCE(SAS),
∴BD=HC=BH﹣BC=3﹣2=1,
∴CD=BH﹣BD﹣HC=3﹣1﹣1=1.
综上所述,CD的长为1或3.
五.等边三角形的判定
26.解:由题可得,CA=CD,BA=BD,
∴CB是AD的垂直平分线,
即CE垂直平分AD,故A选项正确;
∴∠CAD=∠CDA,∠CEA=∠CED,
∴∠ACE=∠DCE,
即CE平分∠ACD,故B选项正确;
∵DB=AB,
∴△ABD是等腰三角形,故C选项正确;
∵AD与AC不一定相等,
∴△ACD不一定是等边三角形,故D选项错误;
故选:D.
27.解:①两个角为60度,则第三个角也是60度,则其是等边三角形;
②有一个角等于60°的等腰三角形是等边三角形;
③三个外角相等,则三个内角相等,则其是等边三角形;
④根据等边三角形的性质,可得该等腰三角形的腰与底边相等,则三角形三边相等.
所以都正确.
故选:A.
六.等边三角形的判定与性质
28.解:如图①
∵△ABC是等边三角形,
∴AB=BC=AC,
∵A′B′∥AB,BB′=B′C=BC,
∴B′O=AB,CO=AC,
∴△B′OC是等边三角形,同理阴影的三角形都是等边三角形.
又观察图可得,第1个图形中大等边三角形有2个,小等边三角形有2个,
第2个图形中大等边三角形有4个,小等边三角形有4个,
第3个图形中大等边三角形有6个,小等边三角形有6个,…
依次可得第n个图形中大等边三角形有2n个,小等边三角形有2n个.
故第100个图形中等边三角形的个数是:2×100+2×100=400.
故答案为:400.
七.含30度角的直角三角形
29.解:①如图,
∵BD是△ABC的高,AB=AC,BD=AB,
∴∠A=30°,
②如图,
∵CD是△ABC边BA 上的高,DC=AC,
∴∠DAC=30°,
∴∠BAC=180°﹣30°=150°,
故答案为:30或150.
30.解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AB=AC,AD是BC边上的中线,
∴∠ADB=90°,
∵BD=BE,
∴∠BDE=75°,
∴∠ADE=15°,
故答案为:15.
31.解:在△ABC中,∵∠C=90°,∠A=30°,
∴∠B=60°.
∵4÷2=2,
∴0≤t≤2,BP=4﹣2t,BQ=t.
(1)当BP=BQ时,△PBQ为等边三角形.
即4﹣2t=t.
∴.
当时,△PBQ为等边三角形;
(2)若△PBQ为直角三角形,
①当∠BQP=90°时,BP=2BQ,
即4﹣2t=2t,
∴t=1.
②当∠BPQ=90°时,BQ=2BP,
即t=2(4﹣2t),
∴.
即当或t=1时,△PBQ为直角三角形.
一.等腰三角形的性质
1.如图,在△ABC中,AB=AC,∠A═55°,点P是AB上的一个动点,则∠APC的度数可能是( )
A.55° B.62° C.80° D.130°
2.等腰△ABC中,∠C=50°,则∠A的度数不可能是( )
A.80° B.50° C.65° D.45°
3.如果等腰三角形的一个角是80°,那么它的底角是( )
A.80°或50° B.50°或20° C.80°或20° D.50°
4.如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点,若∠CAE=16°,则∠B的大小为( )
A.32° B.36° C.37° D.74°
5.等腰三角形一腰上的高与另一腰的夹角为30°,则底角的度数为( )
A.60° B.120° C.60°或120° D.60°或30°
6.已知等腰三角形的两条边长分别是3cm、7cm,那么这个等腰三角形的周长是 cm.
7.已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为 .
8.等腰△ABC的腰AB边上的中线CD,把△ABC的周长分成12和15两部分,则底边BC长为 .
9.规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k,若k=,则该等腰三角形的底角为 .
10.如果等腰三角形有两条边长分别为2cm和3cm,那么它的周长是 .
11.已知等腰三角形的一个内角是50°,则等腰三角形的顶角等于 °.
12.等腰三角形一腰上的高与另一边的夹角为50°,则顶角的度数为 .
13.已知△ABC是等腰三角形.
(1)若∠A=100°,求∠B的度数;
(2)若∠A=70°,求∠B的度数;
(3)若∠A=α(45°<α<90°),过顶点B的角平分线BD与过顶点C的高CE交于点F,求∠BFC的度数(用含α的式子表示).
二.等腰三角形的判定
14.如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
15.已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.
A.3 B.4 C.5 D.6
16.如图是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是( )
A.4 B.5 C.6 D.7
17.如图,在Rt△ABC中,∠ACB=90°,∠CAB=36°,以C为原点,AC所在直线为y轴,BC所在直线为x轴建立平面直角坐标系,在坐标轴上取一点M使△MAB为等腰三角形,符合条件的M点有( )
A.6个 B.7个 C.8个 D.9个
18.如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
A.8个 B.7个 C.6个 D.5个
19.如图,在4×4方格中,以AB为一边,第三个顶点也在格点上的等腰三角形可以作出( )
A.7个 B.6个 C.4个 D.3个
20.如图,A、B两点在正方形网格的格点上,每个方格都是边长为1的正方形、点C也在格点上,且△ABC为等腰三角形,则符合条件的点C共有 个.
三.等腰三角形的判定与性质
21.如图,在△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为 .
四.等边三角形的性质
22.如图,BD为等边△ABC的边AC上的中线,E为BC延长线上一点,且DB=DE,若AB=6cm,则CE= cm.
23.如图,P是边长为4的等边三角形ABC内一点,PD,PE,PF分别垂直于BC,AC,AB,垂足为D,E,F.若PD=BD=1,则PE+PF= ,CE+AF= .
24.数学理解
(1)如图1,在等边△ABC内,作DB=DC,且∠BDC=80°,E是△DBC内一点,且∠CBE=10°,BE=BD,求∠BCE的度数;
联系拓广(联系图1特点,解决下列问题)
(2)如图2,在△DBC中,DB=DC,∠BDC=80°,E是△DBC内一点,且∠CBE=10°,∠BCE=30°,连接DE,求∠CDE的度数.
25.如图,在等边△ABC中,已知点E在直线AB上(不与点A、B重合),点D在直线BC上,且ED=EC.
(1)若点E为线段AB的中点时,试说明DB=AE的理由;
(2)若△ABC的边长为2,AE=1,求CD的长.
五.等边三角形的判定
26.如图,在钝角三角形ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧;再以点C为圆心,AC长为半径画弧;两弧交于点D,连接AD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD B.CE平分∠ACD
C.△ABD是等腰三角形 D.△ACD是等边三角形
27.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③④ B.①②④ C.①③ D.②③④
六.等边三角形的判定与性质
28.如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是 .
七.含30度角的直角三角形
29.等腰三角形腰上的高等于腰长的一半,则这个等腰三角形的顶角为 度.
30.如图,△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,且BD=BE,则∠ADE是 度.
31.如图,在△ABC中,∠C=90°,∠A=30°,AB=4cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
(1)当t为何值时,△PBQ为等边三角形?
(2)当t为何值时,△PBQ为直角三角形?
参考答案
一.等腰三角形的性质
1.解:∵AB=AC,∠A═55°,
∴∠B=∠ACB=62.5°,
∵∠APC是△BCP的外角,
∴∠APC=∠B+∠BCP,
又∵点P是AB上的一个动点,
∴0≤∠BCP≤62.5°,
∴62.5°≤∠APC≤125°,
∴∠APC的度数可能是80°,
故选:C.
2.解:当∠C为顶角时,则∠A=(180°﹣50°)=65°;
当∠A为顶角时,则∠A=180°﹣2∠C=80°;
当∠A、∠C为底角时,则∠C=∠A=50°;
∴∠A的度数不可能是45°,
故选:D.
3.解:根据题意,一个等腰三角形的一个角等于80°,
①当这个角是底角时,即该等腰三角形的底角的度数是80°,
②当这个角80°是顶角,
设等腰三角形的底角是x°,
则2x+80°=180°,
解可得,x=50°,
即该等腰三角形的底角的度数是50°;
故选:A.
4.解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴∠C=90°﹣∠CAE=74°,
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故选:C.
5.解:如图,分两种情况:
①在左图中,AB=AC,BD⊥AC,∠ABD=30°,
∴∠A=60°,
∴∠C=∠ABC==60°;
②在右图中,AB=AC,BD⊥AC,∠ABD=30°,
∴∠DAB=60°,∠BAC=120°,
∴∠C=∠ABC==30°.
故选:D.
6.解:∵等腰三角形的两条边长分别是3cm、7cm,
∴当此三角形的腰长为3cm时,3+3<7,不能构成三角形,故排除,
∴此三角形的腰长为7cm,底边长为3cm,
∴此等腰三角形的周长=7+7+3=17cm,
故答案为:17.
7.解:△ABC,AB=AC.
有两种情况:
(1)顶角∠A=40°,
(2)当底角是40°时,
∵AB=AC,
∴∠B=∠C=40°,
∵∠A+∠B+∠C=180°,
∴∠A=180°﹣40°﹣40°=100°,
∴这个等腰三角形的顶角为40°和100°.
故答案为:40°或100°.
8.解:如图,在△ABC中,AB=AC,且AD=BD.设AB=x,BC=y,
①当AC+AD=15,BD+BC=12时,则x+x=15,x+y=12,
解得x=10,y=7.
②当AC+AD=12,BC+BD=15时,则x+x=12,x+y=15,
解得x=8,y=11,
综上所述,这个三角形的底边BC的长为7或11.
故答案为:7或11.
9.解:∵△ABC中,AB=AC,
∴∠B=∠C,
∵该等腰三角形的顶角与一个底角度数的比值为1:4,
∴∠A:∠B=1:4,
∵∠A+∠B+∠C=180°,
∴∠A+4∠A+4∠A=180°,
即9∠A=180°,
∴∠A=20°,∠B=80°,
故答案为:80°.
10.解:当2是腰时,2,2,3能组成三角形,
周长=3+2+2=7(cm);
当3是腰时,3,3,2能够组成三角形,
周长=3+3+2=8(cm),
综上所述,周长为7cm或8cm,
故答案为:7cm或8cm.
11.解:如图所示,△ABC中,设AB=AC.
分两种情况:
①顶角∠A=50°;
②当底角是50°时,
∵AB=AC,
∴∠B=∠C=50°,
∵∠A+∠B+∠C=180°,
∴∠A=180°﹣50°﹣50°=80°,
综上所述,这个等腰三角形的顶角为50°或80°.
故答案为:50或80.
12.解:△ABC是等腰三角形,且∠BAC为顶角,CD是腰AB的高.
(1)当等腰三角形是锐角三角形时,如图①;
∵∠ACD=50°,
∴∠BAC=90°﹣∠ACD=40°;
(2)当等腰三角形是钝角三角形时;
一、如图②﹣1;
当∠BCD=50°时,∠B=40°;
∴∠BAC=180°﹣2∠B=100°;
二、如图②﹣2;
当∠ACD=50°时,∠CAD=40°;
∴∠BAC=180°﹣∠CAD=140°;
故这个等腰三角形顶角的度数为:100°或140°或40°.
故答案为:100°或140°或40°.
13.解:(1)∵∠A=100°是钝角,
∴∠B=(180°﹣100°)=40°.
故∠B的度数为40°;
(2)若∠A为顶角,则∠B=(180°﹣∠A)÷2=55°;
若∠A为底角,∠B为顶角,则∠B=180°﹣2×70°=40°;
若∠A为底角,∠B为底角,则∠B=70°;
故∠B=55°或40°或70°;
(3)∵∠A=α(45°<α<90°),
①当∠A为顶角时,如图:
∵AB=AC,
∴∠ABC=∠ACB=(180°﹣α),
∵BD平分∠ABC,
∴∠ABD=∠CBD=ABC=(180°﹣α),
∴∠BFC=∠FEB+∠FBE=90°+(180°﹣α)=135°﹣α;
②当∠A为底角,∠B为底角时,如图:
∴∠BFC=∠FEB+∠FBE=90°+;
所以当∠A为底角时,最小值假设取45度,另一个底角也是45度,此时三角形ABC是直角三角形,
但是∠A 大于45°,所以两个底角的和一定大于90度,所以三角形ABC不可能是钝角三角形,
所以此种情况不存在.
当∠A为底角,∠B为底角时,∠C为顶角且为锐角时,如图:
∴∠BFC=∠FEB+∠FBE=90°+;
③当∠A为底角,∠B为顶角时,如图:
∵∠BFC+∠FBE=90°,
∠A+∠ABD=90°,
∵∠FBE=∠ABD,
∴∠BFC=∠A=α.
∵∠A 大于45°,所以等腰三角形ABC一定是锐角三角形,
∴此种情况不符合题意;
当A为底角,三角形是锐角三角形时,
如图,
∵AB=BC,BD平分∠ABC,
∴BD⊥AC,
∴∠ADF=90°,
∵CE⊥AB,
∴∠AEF=90°,
根据四边形内角和定理,得
∴∠BFC=180﹣a.
故∠BFC的度数为:135°﹣α;90°+;180°﹣α.
二.等腰三角形的判定
14.解:①AB为等腰△ABC底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
15.解:如图所示:
当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形(AD,AE,AF,AG分别为分割线).
故选:B.
16.解:如图所示:
C在C1,C2,C3,C4位置上时,AC=BC;
C在C5,C6位置上时,AB=BC;
即满足点C的个数是6,
故选:C.
17.解:如图,
①以A为圆心,AB为半径画圆,交直线AC有二点M1,M2,交BC有一点M3,(此时AB=AM);
②以B为圆心,BA为半径画圆,交直线BC有二点M5,M4,交AC有一点M6(此时BM=BA).
③AB的垂直平分线交AC一点M7(MA=MB),交直线BC于点M8;
∴符合条件的点有8个.
故选:C.
18.解:当AB为底时,作AB的垂直平分线,可找出格点C的个数有5个,
当AB为腰时,分别以A、B点为顶点,以AB为半径作弧,可找出格点C的个数有3个;
∴这样的顶点C有8个.
故选:A.
19.解:如图所示,分别以A、B为圆心,AB长为半径画弧,则圆弧经过的格点C1、C2、C3、C4、C5、C6、C7即为第三个顶点的位置;作线段AB的垂直平分线,垂直平分线未经过网格中的格点.
故以AB为一边,第三个顶点也在格点上的等腰三角形可以作出7个.
故选:A.
20.解:①点C以点A为标准,AB为底边,符合点C的有5个;
②点C以点B为标准,AB为等腰三角形的一条边,符合点C的有4个.
所以符合条件的点C共有9个.
三.等腰三角形的判定与性质
21.解:过E作EG∥AB,交AC于G,则∠BAE=∠AEG,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴∠CAE=∠AEG,
∴AG=EG,
同理可得,EF=CF,
∵AB∥GE,BC∥EF,
∴∠BAC=∠EGF,∠BCA=∠EFG,
∵∠ABC=90°,AB=6,BC=8,
∴AC=10,
∴EG:EF:GF=AB:BC:AC=3:4:5,
设EG=3k=AG,则EF=4k=CF,FG=5k,
∵AC=10,
∴3k+5k+4k=10,
∴k=,
∴EF=4k=.
故答案为:.
四.等边三角形的性质
22.解:∵BD为等边△ABC的边AC上的中线,∴BD⊥AC,
∵DB=DE,∴∠DBC=∠E=30°
∵∠ACB=∠E+∠CDE=60°
∴∠CDE=30°
∴∠CDE=∠E,
即CE=CD=AC=3cm.
故填3.
23.解:过A作AG⊥BC于G,
∵△ABC是等边三角形,
∴CG=BC=2,
∴AG=2,
连接PA、PB、PC,
∵PD,PE,PF分别垂直于BC,AC,AB,
∴S△ABC=S△APB+S△PBC+S△APC,
+,
AB=AB(PE+1+PF),
∴PE+PF=2﹣1,
延长DP交AB于H,
∵PF⊥AB,PD⊥BC,
∴∠BFP=∠BDP=90°,
∵∠ABC=60°,
∴∠HFP=60°,
∴∠BHD=30°,
∵BD=1,
∴BH=2,DH=,
∵PD=1,
∴PH=﹣1,
Rt△PFH中,PF=,
∴FH==,
∴BF=BH﹣FH=2﹣=,
∴AF=4﹣BF=,
∵PE+PF=2﹣1,
∴PE=2﹣1﹣=,
Rt△PDC中,PC===,
∴CE====,
∴CE+AF==5
故答案为:2﹣1,5
24.解:(1)如图1,连接AD,
∵AB=AC,DB=DC,
∴直线AD是线段BC的垂直平分线,
∴AD平分∠BAC,
∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∴∠BAD=30°,
∵∠BDC=80°,
∴∠DBC=50°,
∴∠ABD=60°﹣50°=10°=∠CBE,
又∵AB=BC,BE=BD,
∴△ABD≌△CBE(SAS),
∴∠BCE=∠BAD=30°;
(2)如图2,作等边三角形ABC,连接AD,
由(1)解答知,∠BAD=∠BCE=30°,∠ABD=∠CBE=10°,
∴△ABD≌△CBE(SAS),
∴BD=BE,
∵∠DBE=60°﹣10°﹣10°=40°,
∴∠BDE=70°,
∴∠CDE=∠BDC﹣∠BDE=80°﹣70°=10°.
25.解:(1)∵△ABC是等边三角形,E为AB的中点,
∴∠BCE=30°,BE=AE,
∵ED=EC,
∴∠EDB=∠BCE=30°,
∵∠ABD=120°,
∴∠DEB=30°,
∴DB=EB,
∴AE=DB;
(2)如图1,E在线段AB上时,
∵AB=2,AE=1,
∴点E是AB的中点,
由(1)知,BD=AE=1,
∴CD=BC+BD=3;
如图2,E在线段AB的反向延长线上时,
∵AE=1,AB=2,
∴BE=3,
∵△ABC是等边三角形,
∴∠BAC=∠BCA=60°,AB=BC=AC=2,
过E作EH∥AC交BC的延长线于H,
∴∠BEH=∠BHE=60°,
∴△BEH是等边三角形,
∴BE=EH=BH=3,∠B=∠H=60°,
∵ED=EC,
∴∠EDC=∠ECD,
∴∠B+∠BED=∠H+∠HEC,
∴∠BED=∠HEC,
在△BDE和△HCE中,
,
∴△BDE≌△HCE(SAS),
∴BD=HC=BH﹣BC=3﹣2=1,
∴CD=BH﹣BD﹣HC=3﹣1﹣1=1.
综上所述,CD的长为1或3.
五.等边三角形的判定
26.解:由题可得,CA=CD,BA=BD,
∴CB是AD的垂直平分线,
即CE垂直平分AD,故A选项正确;
∴∠CAD=∠CDA,∠CEA=∠CED,
∴∠ACE=∠DCE,
即CE平分∠ACD,故B选项正确;
∵DB=AB,
∴△ABD是等腰三角形,故C选项正确;
∵AD与AC不一定相等,
∴△ACD不一定是等边三角形,故D选项错误;
故选:D.
27.解:①两个角为60度,则第三个角也是60度,则其是等边三角形;
②有一个角等于60°的等腰三角形是等边三角形;
③三个外角相等,则三个内角相等,则其是等边三角形;
④根据等边三角形的性质,可得该等腰三角形的腰与底边相等,则三角形三边相等.
所以都正确.
故选:A.
六.等边三角形的判定与性质
28.解:如图①
∵△ABC是等边三角形,
∴AB=BC=AC,
∵A′B′∥AB,BB′=B′C=BC,
∴B′O=AB,CO=AC,
∴△B′OC是等边三角形,同理阴影的三角形都是等边三角形.
又观察图可得,第1个图形中大等边三角形有2个,小等边三角形有2个,
第2个图形中大等边三角形有4个,小等边三角形有4个,
第3个图形中大等边三角形有6个,小等边三角形有6个,…
依次可得第n个图形中大等边三角形有2n个,小等边三角形有2n个.
故第100个图形中等边三角形的个数是:2×100+2×100=400.
故答案为:400.
七.含30度角的直角三角形
29.解:①如图,
∵BD是△ABC的高,AB=AC,BD=AB,
∴∠A=30°,
②如图,
∵CD是△ABC边BA 上的高,DC=AC,
∴∠DAC=30°,
∴∠BAC=180°﹣30°=150°,
故答案为:30或150.
30.解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AB=AC,AD是BC边上的中线,
∴∠ADB=90°,
∵BD=BE,
∴∠BDE=75°,
∴∠ADE=15°,
故答案为:15.
31.解:在△ABC中,∵∠C=90°,∠A=30°,
∴∠B=60°.
∵4÷2=2,
∴0≤t≤2,BP=4﹣2t,BQ=t.
(1)当BP=BQ时,△PBQ为等边三角形.
即4﹣2t=t.
∴.
当时,△PBQ为等边三角形;
(2)若△PBQ为直角三角形,
①当∠BQP=90°时,BP=2BQ,
即4﹣2t=2t,
∴t=1.
②当∠BPQ=90°时,BQ=2BP,
即t=2(4﹣2t),
∴.
即当或t=1时,△PBQ为直角三角形.
同课章节目录
