2.4线段的垂直平分线 同步能力达标测评 2021-2022学年湘教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 2.4线段的垂直平分线 同步能力达标测评 2021-2022学年湘教版八年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 259.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 18:51:52 | ||
图片预览



文档简介
2021-2022年湘教版八年级数学上册《2.4线段的垂直平分线》同步能力达标测评(附答案)
一.选择题(共7小题,满分28分)
1.如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在AC,BC两边高线的交点处 B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处 D.在∠A,∠B两内角平分线的交点处
2.如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( )
A.6cm B.8cm C.10cm D.12cm
3.如图,△ABC中,∠A=40°,边AC的垂直平分线DE交AB、AC于点D、E,且∠ACD:∠BCD=2:1,则∠ACB的度数为( )
A.20° B.40° C.60° D.80°
4.如图,△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E,已知∠C=38°,则∠BAE的度数为( )
A.13° B.14° C.15° D.16°
5.如图,△ABC中,AB=6cm,AC=8cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为( )
A.10cm B.12cm C.14cm D.16cm
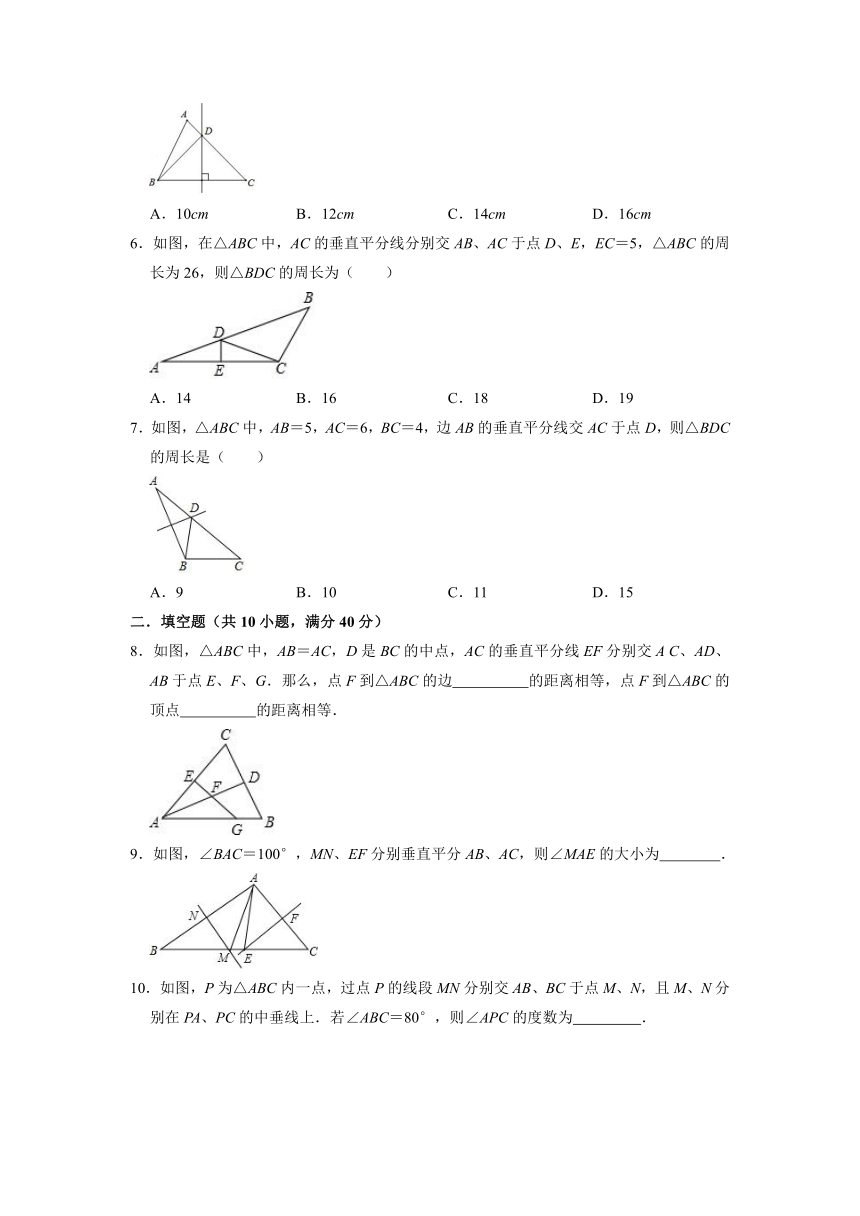
6.如图,在△ABC中,AC的垂直平分线分别交AB、AC于点D、E,EC=5,△ABC的周长为26,则△BDC的周长为( )
A.14 B.16 C.18 D.19
7.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
A.9 B.10 C.11 D.15
二.填空题(共10小题,满分40分)
8.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线EF分别交A C、AD、AB于点E、F、G.那么,点F到△ABC的边 的距离相等,点F到△ABC的顶点 的距离相等.
9.如图,∠BAC=100°,MN、EF分别垂直平分AB、AC,则∠MAE的大小为 .
10.如图,P为△ABC内一点,过点P的线段MN分别交AB、BC于点M、N,且M、N分别在PA、PC的中垂线上.若∠ABC=80°,则∠APC的度数为 .
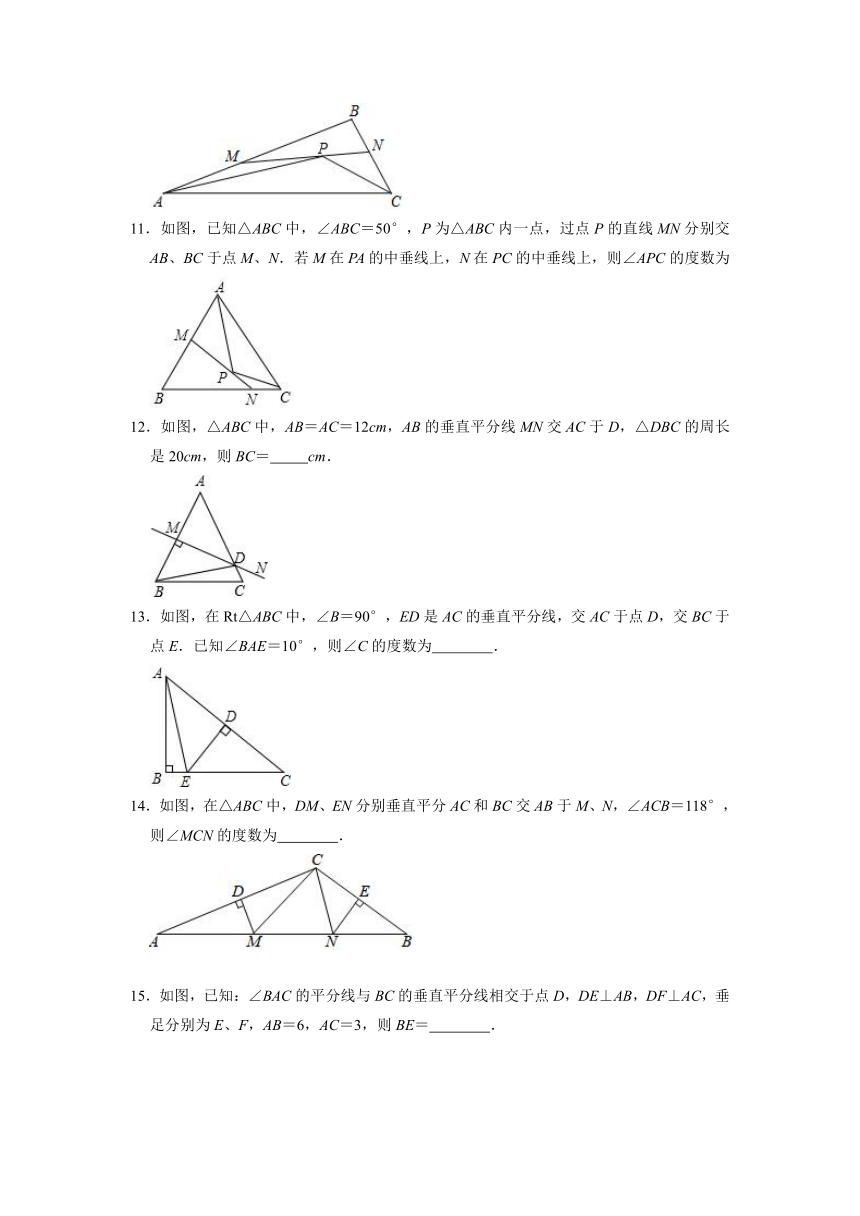
11.如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分别交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为
12.如图,△ABC中,AB=AC=12cm,AB的垂直平分线MN交AC于D,△DBC的周长是20cm,则BC= cm.
13.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为 .
14.如图,在△ABC中,DM、EN分别垂直平分AC和BC交AB于M、N,∠ACB=118°,则∠MCN的度数为 .
15.如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE= .
16.在△ABC中,AB=6,BC=8,AC的垂直平分线交BC于点D,交AC于E,△ABD的周长为 .
17.如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长= ,∠EFC= 度.
三.解答题(共7小题,满分52分)
18.如图,△ABC中,∠C=90°,DE垂直平分AB,若∠B=25°,求∠CAE的度数.
19.如图,点P为△ABC三边垂直平分线的交点,∠PAC=20°,∠PCB=30°,
(1)求∠PAB的度数;
(2)直接写出∠APB与∠ACB的数量关系.
20.如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF.
21.两两相交的三条公路经过A、B、C三个村庄.
(1)要建一个水电站P到三个村庄的距离相等,请通过画图确定点P的位置.
(2)要建一个加油站Q,使加油站Q到三条公路的距离相等,这样的加油站Q的位置有 处.
22.已知直线l及其两侧两点A、B,如图.
(1)在直线l上求一点P,使PA=PB;
(2)在直线l上求一点Q,使l平分∠AQB.
(以上两小题保留作图痕迹,标出必要的字母,不要求写作法)
23.如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
24.在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图①,若∠BAC=110°,求∠EAN的度数;
(2)如图②,若∠BAC=80°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
参考答案
一.选择题(共7小题,满分28分)
1.解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等.
则超市应建在AC,BC两边垂直平分线的交点处.
故选:C.
2.解:∵DE是边AB的垂直平分线,
∴AE=BE.
∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=18.
又∵BC=8,
∴AC=10(cm).
故选:C.
3.解:如图,∵DE垂直平分AC,
∴CD=AD,
∴∠A=∠ACD=40°.
又∵∠ACD:∠BCD=2:1,
∴∠BCD=20°,
∴∠ACB=∠ACD+∠BCD=60°.
故选:C.
4.解:∵ED是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C=38°,
∵∠C=38°,∠B=90°,
∴∠BAC=52°,
∴∠BAE=∠BAC﹣∠CAE=14°,
故选:B.
5.解:∵BC的垂直平分线l与AC相交于点D,
∴DB=DC,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=14(cm),
故选:C.
6.解:∵DE是AC的垂直平分线,
∴DA=DC,AC=2EC=10,
∵△ABC的周长为26,
∴AB+AC+BC=26,
∴AB+BC=16,
∴△BDC的周长=BD+CD+BC=BD+AD+BC=AB+BC=16,
故选:B.
7.解:∵ED是AB的垂直平分线,
∴AD=BD,
∵△BDC的周长=DB+BC+CD,
∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10.
故选:B.
二.填空题(共10小题,满分40分)
8.解:∵AB=AC,D是BC的中点,
∴AD平分∠BAC,AD垂直平分BC.
∵点F在AD上,
∴点F到AC、AB的距离相等;
∵EF垂直平分AC,AD垂直平分BC.
∴FA=FB=FC,即点F到A、B、C的距离相等.
故答案为 AC、AB; A、B、C.
9.解:∵∠BAC=100°,
∴∠B+∠C=180°﹣∠BAC=80°,
∵MN、EF分别垂直平分AB、AC,
∴BM=AM,CE=AE,
∴∠MAB=∠B,∠EAC=∠C,
∴∠MAB+∠EAC=∠B+∠C=80°,
∴∠MAE=∠BAC﹣(∠MAB+∠EAC)=100°﹣80°=20°,
故答案为:20°.
10.解:∵∠ABC=80°,
∴∠BMN+∠BNM=100°,
∵M、N分别在PA、PC的中垂线上,
∴MA=MP,NP=NC,
∴∠MPA=∠MAP=∠BMN,∠NPC=∠NCP=∠BNM,
∴∠MPA+∠NPC=×100°=50°,
∴∠APC=180°﹣50°=130°,
故答案为:130°.
11.解:∵∠B+∠BMN+∠BNM=180°,
∴∠BMN+∠BNM=180°﹣50°=130°,
∵M在PA的中垂线上,
∴MA=MP,
∴∠MAP=∠MPA,
同理,∠NCP=∠NPC,
∵∠BMN=∠MAP+∠MPA,∠BNM=∠NPC+∠NCP,
∴∠MPA+∠NPC=×130°=65°,
∴∠APC=180°﹣65°=115°,
故答案为:115°.
12.解:∵MN是AB的垂直平分线,
∴AD=BD,
∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC,
∵△DBC的周长是20cm,AC=12cm,
∴12+BC=20,
解得BC=8cm.
故答案为:8.
13.解:∵∠B=90°,∠BAE=10°,
∴∠BEA=80°.
∵ED是AC的垂直平分线,
∴AE=EC,
∴∠C=∠EAC.
∵∠BEA=∠C+∠EAC,
∴∠C=40°.
故答案为:40°.
14.解:∵∠ACB=118°,
∴∠A+∠B=62°.
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠ACM+∠BCN=62°.
∴∠MCN=∠ACB﹣(∠ACM+∠BCN)=118°﹣62°=56°.
故答案为:56°.
15.解:连接CD,BD,
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,
∴AE=AF,
∵DG是BC的垂直平分线,
∴CD=BD,
在Rt△CDF和Rt△BDE中,
,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
∵AB=6,AC=3,
∴BE=1.5.
故答案为:1.5.
16.解:∵边AC的垂直平分线交BC于点D,交AC于点E,
∴AD=DC,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=6+8=14,
故答案为:14.
17.解:如图:已知DF垂直且平分AB AF=BF,AD=BD,∠A=∠ABF=50°,∠ADF=90°
∠EFC=180°﹣∠A﹣∠ADF=40°(对角相等)
因为AB+BC=6,AB=AC=BF+FC
故周长△BCF=FC+BF+BC=6.
故填6;40°.
三.解答题(共7小题,满分52分)
18.解:∵DE垂直平分AB,
∴EA=EB,
∵∠B=25°,
∴∠EAB=∠B=25°,
∵∠C=90°,
∴∠CAB=65°,
∴∠CAE=65°﹣25°=40°.
19.解:(1)∵P为△ABC三边垂直平分线的交点,
∴PA=PC=PB,
∴∠PAC=∠PCA=20°,
∠PBC=∠PCB=30°,
∵∠PAB=∠PBA,
∴∠PAB=(180°﹣2×20°﹣2×30°)=40°.
(2)∵∠APB=180°﹣40°﹣40°=100°,∠ACB=∠ACP+∠PCB=50°,
∴∠APB=2∠ACB.
故答案为∠APB=2∠ACB.
20.证:∵AD是∠BAC的平分线,
DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AD是∠BAC的平分线,
∴AD垂直平分EF.
21.解:(1)如图,由于“线段垂直平分线上的点到线段两端的距离相等”,
分别作AB、BC、CA边的垂直平分线,相交于P,P即为所求.
(2)如图,由于“角平分线上的点到角的两边的距离相等”,
分别作∠ABC、∠BCA、∠CAB的平分线相交于P1,
∠IAE和∠DCA的平分线相交于P2,
∠ECB和∠FBC的平分线相交于P3,
∠HAB和∠GBH的平分线相交于P4.
故加油站Q的位置有4处.
22.解:
23.解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=12cm;
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=32cm,
∴OA=OB=OC=10cm;
(3)∵∠BAC=n°,
∴∠ABC+∠ACB=(180﹣n)°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=n°﹣(180°﹣n°)=2n°﹣180°.
故答案为:(2n﹣180).
24.解:(1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得∠CAN=∠C,
∴∠EAN=∠BAC﹣∠BAE﹣∠CAN=∠BAC﹣(∠B+∠C),
在△ABC中,∠B+∠C=180°﹣∠BAC=70°,
∴∠EAN=110°﹣70°=40°.
(2)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN﹣∠BAC=(∠B+∠C)﹣∠BAC,
在△ABC中,∠B+∠C=180°﹣∠BAC=100°,
∴∠EAN=100°﹣80°=20°.
(3)当0°<α<90°时,∠EAN=180°﹣2α;
当90°<α<180°时,∠EAN=2α﹣180°.
一.选择题(共7小题,满分28分)
1.如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在AC,BC两边高线的交点处 B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处 D.在∠A,∠B两内角平分线的交点处
2.如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( )
A.6cm B.8cm C.10cm D.12cm
3.如图,△ABC中,∠A=40°,边AC的垂直平分线DE交AB、AC于点D、E,且∠ACD:∠BCD=2:1,则∠ACB的度数为( )
A.20° B.40° C.60° D.80°
4.如图,△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E,已知∠C=38°,则∠BAE的度数为( )
A.13° B.14° C.15° D.16°
5.如图,△ABC中,AB=6cm,AC=8cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为( )
A.10cm B.12cm C.14cm D.16cm
6.如图,在△ABC中,AC的垂直平分线分别交AB、AC于点D、E,EC=5,△ABC的周长为26,则△BDC的周长为( )
A.14 B.16 C.18 D.19
7.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
A.9 B.10 C.11 D.15
二.填空题(共10小题,满分40分)
8.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线EF分别交A C、AD、AB于点E、F、G.那么,点F到△ABC的边 的距离相等,点F到△ABC的顶点 的距离相等.
9.如图,∠BAC=100°,MN、EF分别垂直平分AB、AC,则∠MAE的大小为 .
10.如图,P为△ABC内一点,过点P的线段MN分别交AB、BC于点M、N,且M、N分别在PA、PC的中垂线上.若∠ABC=80°,则∠APC的度数为 .
11.如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分别交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为
12.如图,△ABC中,AB=AC=12cm,AB的垂直平分线MN交AC于D,△DBC的周长是20cm,则BC= cm.
13.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为 .
14.如图,在△ABC中,DM、EN分别垂直平分AC和BC交AB于M、N,∠ACB=118°,则∠MCN的度数为 .
15.如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE= .
16.在△ABC中,AB=6,BC=8,AC的垂直平分线交BC于点D,交AC于E,△ABD的周长为 .
17.如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长= ,∠EFC= 度.
三.解答题(共7小题,满分52分)
18.如图,△ABC中,∠C=90°,DE垂直平分AB,若∠B=25°,求∠CAE的度数.
19.如图,点P为△ABC三边垂直平分线的交点,∠PAC=20°,∠PCB=30°,
(1)求∠PAB的度数;
(2)直接写出∠APB与∠ACB的数量关系.
20.如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF.
21.两两相交的三条公路经过A、B、C三个村庄.
(1)要建一个水电站P到三个村庄的距离相等,请通过画图确定点P的位置.
(2)要建一个加油站Q,使加油站Q到三条公路的距离相等,这样的加油站Q的位置有 处.
22.已知直线l及其两侧两点A、B,如图.
(1)在直线l上求一点P,使PA=PB;
(2)在直线l上求一点Q,使l平分∠AQB.
(以上两小题保留作图痕迹,标出必要的字母,不要求写作法)
23.如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
24.在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图①,若∠BAC=110°,求∠EAN的度数;
(2)如图②,若∠BAC=80°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
参考答案
一.选择题(共7小题,满分28分)
1.解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等.
则超市应建在AC,BC两边垂直平分线的交点处.
故选:C.
2.解:∵DE是边AB的垂直平分线,
∴AE=BE.
∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=18.
又∵BC=8,
∴AC=10(cm).
故选:C.
3.解:如图,∵DE垂直平分AC,
∴CD=AD,
∴∠A=∠ACD=40°.
又∵∠ACD:∠BCD=2:1,
∴∠BCD=20°,
∴∠ACB=∠ACD+∠BCD=60°.
故选:C.
4.解:∵ED是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C=38°,
∵∠C=38°,∠B=90°,
∴∠BAC=52°,
∴∠BAE=∠BAC﹣∠CAE=14°,
故选:B.
5.解:∵BC的垂直平分线l与AC相交于点D,
∴DB=DC,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=14(cm),
故选:C.
6.解:∵DE是AC的垂直平分线,
∴DA=DC,AC=2EC=10,
∵△ABC的周长为26,
∴AB+AC+BC=26,
∴AB+BC=16,
∴△BDC的周长=BD+CD+BC=BD+AD+BC=AB+BC=16,
故选:B.
7.解:∵ED是AB的垂直平分线,
∴AD=BD,
∵△BDC的周长=DB+BC+CD,
∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10.
故选:B.
二.填空题(共10小题,满分40分)
8.解:∵AB=AC,D是BC的中点,
∴AD平分∠BAC,AD垂直平分BC.
∵点F在AD上,
∴点F到AC、AB的距离相等;
∵EF垂直平分AC,AD垂直平分BC.
∴FA=FB=FC,即点F到A、B、C的距离相等.
故答案为 AC、AB; A、B、C.
9.解:∵∠BAC=100°,
∴∠B+∠C=180°﹣∠BAC=80°,
∵MN、EF分别垂直平分AB、AC,
∴BM=AM,CE=AE,
∴∠MAB=∠B,∠EAC=∠C,
∴∠MAB+∠EAC=∠B+∠C=80°,
∴∠MAE=∠BAC﹣(∠MAB+∠EAC)=100°﹣80°=20°,
故答案为:20°.
10.解:∵∠ABC=80°,
∴∠BMN+∠BNM=100°,
∵M、N分别在PA、PC的中垂线上,
∴MA=MP,NP=NC,
∴∠MPA=∠MAP=∠BMN,∠NPC=∠NCP=∠BNM,
∴∠MPA+∠NPC=×100°=50°,
∴∠APC=180°﹣50°=130°,
故答案为:130°.
11.解:∵∠B+∠BMN+∠BNM=180°,
∴∠BMN+∠BNM=180°﹣50°=130°,
∵M在PA的中垂线上,
∴MA=MP,
∴∠MAP=∠MPA,
同理,∠NCP=∠NPC,
∵∠BMN=∠MAP+∠MPA,∠BNM=∠NPC+∠NCP,
∴∠MPA+∠NPC=×130°=65°,
∴∠APC=180°﹣65°=115°,
故答案为:115°.
12.解:∵MN是AB的垂直平分线,
∴AD=BD,
∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC,
∵△DBC的周长是20cm,AC=12cm,
∴12+BC=20,
解得BC=8cm.
故答案为:8.
13.解:∵∠B=90°,∠BAE=10°,
∴∠BEA=80°.
∵ED是AC的垂直平分线,
∴AE=EC,
∴∠C=∠EAC.
∵∠BEA=∠C+∠EAC,
∴∠C=40°.
故答案为:40°.
14.解:∵∠ACB=118°,
∴∠A+∠B=62°.
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠ACM+∠BCN=62°.
∴∠MCN=∠ACB﹣(∠ACM+∠BCN)=118°﹣62°=56°.
故答案为:56°.
15.解:连接CD,BD,
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,
∴AE=AF,
∵DG是BC的垂直平分线,
∴CD=BD,
在Rt△CDF和Rt△BDE中,
,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
∵AB=6,AC=3,
∴BE=1.5.
故答案为:1.5.
16.解:∵边AC的垂直平分线交BC于点D,交AC于点E,
∴AD=DC,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=6+8=14,
故答案为:14.
17.解:如图:已知DF垂直且平分AB AF=BF,AD=BD,∠A=∠ABF=50°,∠ADF=90°
∠EFC=180°﹣∠A﹣∠ADF=40°(对角相等)
因为AB+BC=6,AB=AC=BF+FC
故周长△BCF=FC+BF+BC=6.
故填6;40°.
三.解答题(共7小题,满分52分)
18.解:∵DE垂直平分AB,
∴EA=EB,
∵∠B=25°,
∴∠EAB=∠B=25°,
∵∠C=90°,
∴∠CAB=65°,
∴∠CAE=65°﹣25°=40°.
19.解:(1)∵P为△ABC三边垂直平分线的交点,
∴PA=PC=PB,
∴∠PAC=∠PCA=20°,
∠PBC=∠PCB=30°,
∵∠PAB=∠PBA,
∴∠PAB=(180°﹣2×20°﹣2×30°)=40°.
(2)∵∠APB=180°﹣40°﹣40°=100°,∠ACB=∠ACP+∠PCB=50°,
∴∠APB=2∠ACB.
故答案为∠APB=2∠ACB.
20.证:∵AD是∠BAC的平分线,
DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AD是∠BAC的平分线,
∴AD垂直平分EF.
21.解:(1)如图,由于“线段垂直平分线上的点到线段两端的距离相等”,
分别作AB、BC、CA边的垂直平分线,相交于P,P即为所求.
(2)如图,由于“角平分线上的点到角的两边的距离相等”,
分别作∠ABC、∠BCA、∠CAB的平分线相交于P1,
∠IAE和∠DCA的平分线相交于P2,
∠ECB和∠FBC的平分线相交于P3,
∠HAB和∠GBH的平分线相交于P4.
故加油站Q的位置有4处.
22.解:
23.解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=12cm;
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=32cm,
∴OA=OB=OC=10cm;
(3)∵∠BAC=n°,
∴∠ABC+∠ACB=(180﹣n)°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=n°﹣(180°﹣n°)=2n°﹣180°.
故答案为:(2n﹣180).
24.解:(1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得∠CAN=∠C,
∴∠EAN=∠BAC﹣∠BAE﹣∠CAN=∠BAC﹣(∠B+∠C),
在△ABC中,∠B+∠C=180°﹣∠BAC=70°,
∴∠EAN=110°﹣70°=40°.
(2)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN﹣∠BAC=(∠B+∠C)﹣∠BAC,
在△ABC中,∠B+∠C=180°﹣∠BAC=100°,
∴∠EAN=100°﹣80°=20°.
(3)当0°<α<90°时,∠EAN=180°﹣2α;
当90°<α<180°时,∠EAN=2α﹣180°.
同课章节目录
