2.5全等三角形 同步优生辅导训练 2021-2022学年湘教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 2.5全等三角形 同步优生辅导训练 2021-2022学年湘教版八年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 434.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 18:54:39 | ||
图片预览



文档简介
2021-2022学年湘教版八年级数学上册《2.5全等三角形》同步优生辅导训练(附答案)
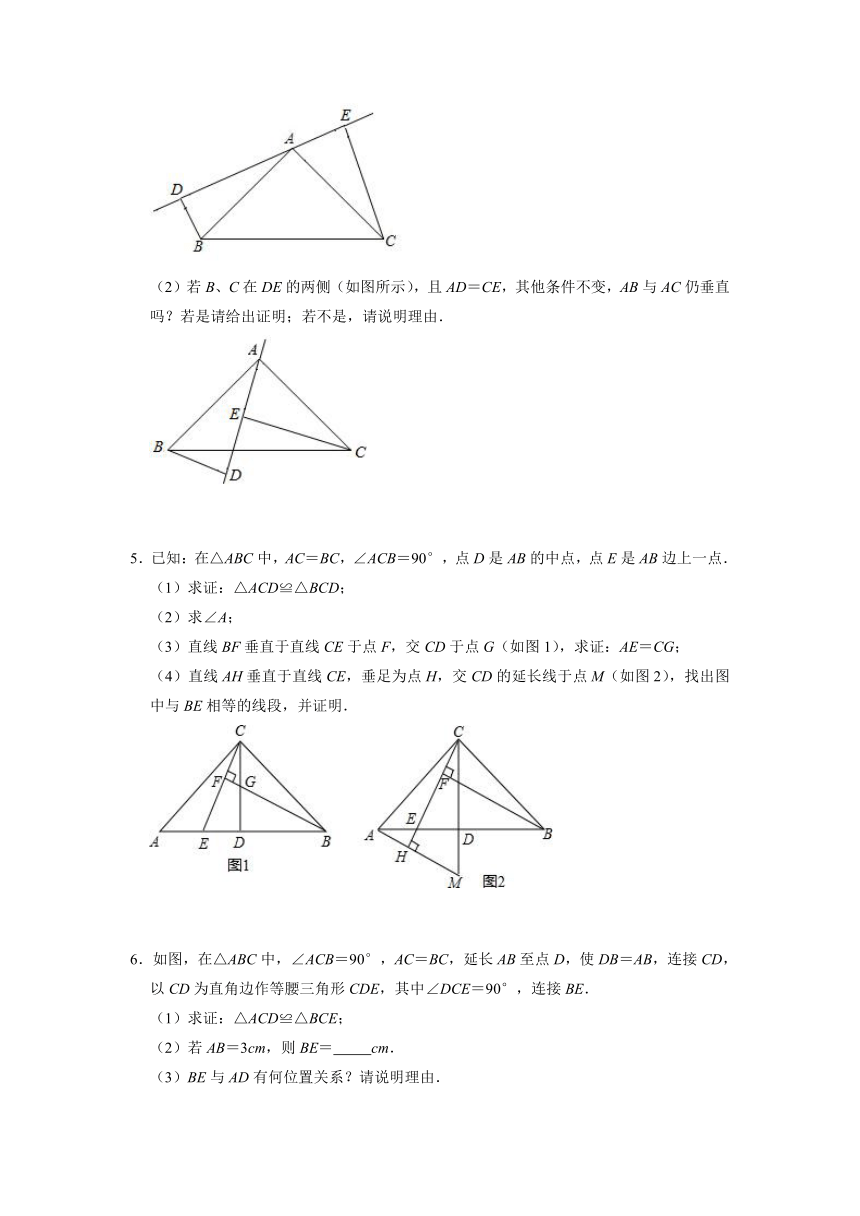
1.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AO上运动,当AP= 时,△ABC和△PQA全等.
2.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
3.小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.6m和2m,∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由;
(2)爸爸是在距离地面多高的地方接住小明的?
4.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
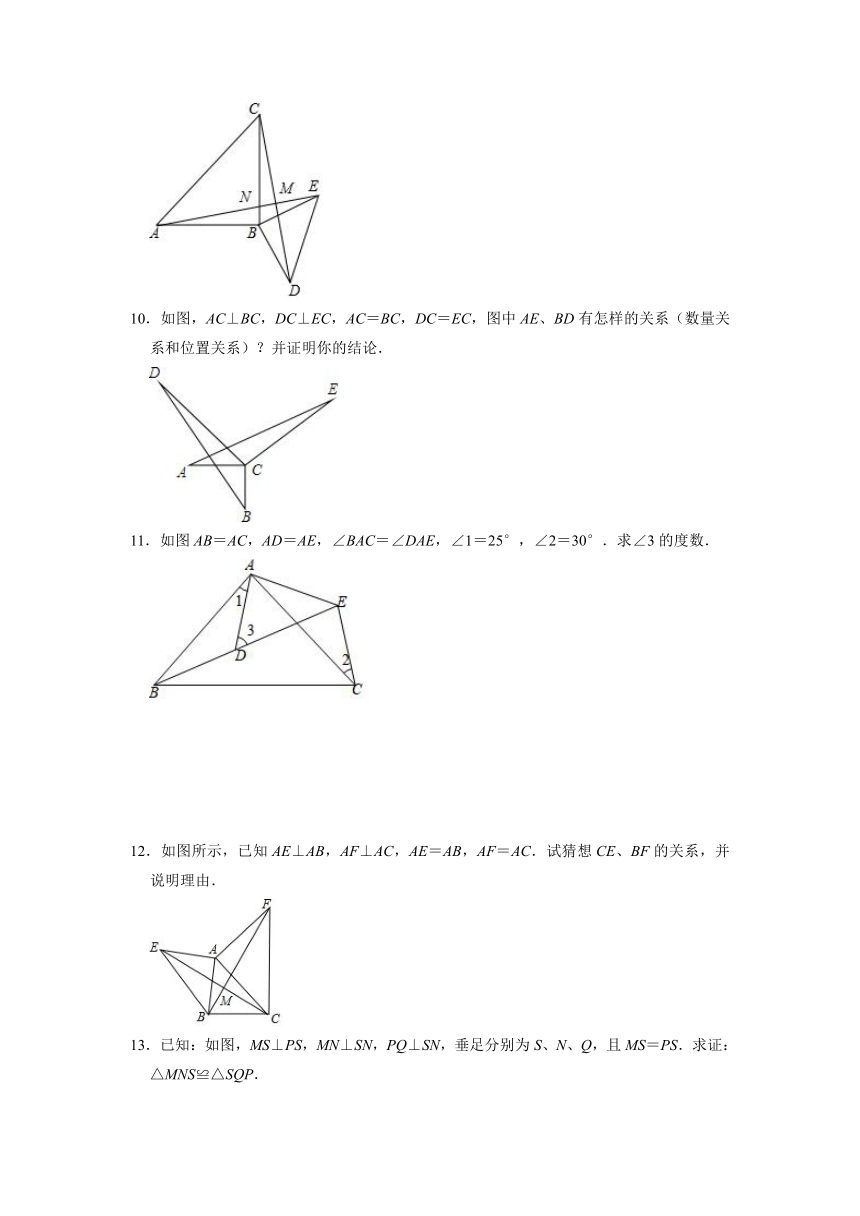
5.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)求证:△ACD≌△BCD;
(2)求∠A;
(3)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(4)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
6.如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AB=3cm,则BE= cm.
(3)BE与AD有何位置关系?请说明理由.
7.如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
(1)求证:△CBD≌△CA1F;
(2)试用含α的代数式表示∠B1BD;
(3)当α等于多少度时,△BB1D是等腰三角形.
8.如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
9.如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).
10.如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,图中AE、BD有怎样的关系(数量关系和位置关系)?并证明你的结论.
11.如图AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°.求∠3的度数.
12.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.试猜想CE、BF的关系,并说明理由.
13.已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,且MS=PS.求证:△MNS≌△SQP.
14.已知:如图,CB⊥AD,AE⊥DC,垂足分别B、E,AE、BC相交于点F,且AB=BC.求证:△ABF≌△CBD.
15.在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连接BD,E、F分别是AB、BC上的点,且DE⊥DF.(1)如图1,若D为AC边上的中点.
①填空:∠C= ,∠DBC= ;
②求证:△BDE≌△CDF.
(2)如图2,D从点C出发,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤t≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.
16.如图(1),△ABC中,BC=AC,△CDE中,CE=CD,现把两个三角形的C点重合,且使∠BCA=∠ECD,连接BE,AD.求证:BE=AD.
若将△DEC绕点C旋转至图(2),(3)所示的情况时,其余条件不变,BE与AD还相等吗?利用图(3)说明理由.
17.(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
18.如图,在△ABC中,∠B=∠C,AB=8,BC=6,点D为AB的中点,点P在线段BC上以每秒2个单位的速度由点B向点C运动,同时点Q在线段CA上以每秒a个单位的速度由点C向点A运动,设运动时间为t(秒)(0≤t≤3).
(1)用含t的代数式表示线段PC的长;
(2)若点P、Q的运动速度相等,t=1时,△BPD与△CQP是否全等,请说明理由.
(3)若点P、Q的运动速度不相等,△BPD与△CQP全等时,求a的值.
19.已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.
20.(1)问题背景:
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点且∠EAF=
60°,探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
(3)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
参考答案
1.解:∵∠ACB=∠PAQ=90°,PQ=AB,
∴当AP=CB=5时,Rt△PQA≌Rt△BAC;
当AP=CA=10时,Rt△PQA≌Rt△ABC;
即AP为5或10时,△ABC和△PQA全等.
故答案为5或10.
2.解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
3.解:(1)△OBD与△COE全等.
理由如下:
由题意可知∠CEO=∠BDO=90°,OB=OC,
∵∠BOC=90°,
∴∠COE+∠BOD=∠BOD+∠OBD=90°.
∴∠COE=∠OBD,
在△COE和△OBD中,
,
∴△COE≌△OBD(AAS);
(2)∵△COE≌△OBD,
∴CE=OD,OE=BD,
∵BD、CE分别为1.6m和2m,
∴DE=OD﹣OE=CE﹣BD=2﹣1.6=0.4(m),
∵AD=1.2m,
∴AE=AD+DE=1.6(m),
答:爸爸是在距离地面1.6m的地方接住小明的.
4.(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
5.(1)证明:如图,∵D是AB的中点,
∴AD=BD.
∵在△ACD与△BCD中,,
∴△ACD≌△BCD(SSS);
(2)解:如图,∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠ABC,∠A+∠ABC=90°,
∴∠A=∠ABC=45°,即∠A=45°;
(3)证明:如图1,∵点D是AB中点,AC=BC,
∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,,
∴△AEC≌△CGB(ASA),
∴AE=CG;
(4)解:BE=CM.理由如下:
∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,,
∴△BCE≌△CAM(AAS),
∴BE=CM.
6.(1)证明:∵△ACB和△DCE都是等腰直角三角形,
∴CD=CE,CA=CB,
∵∠ACB=90°,∠DCE=90°,
∴∠ECD+∠DCB=∠DCB+∠ACB,即∠ECB=∠ACD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
(2)解:∵△ACD≌△BCE,
∴AD=BE,
∵DB=AB=3cm,
∴BE=2×3cm=6cm;
(3)解:BE与AD垂直.理由如下:
∵△ACD≌△BCE,
∴∠1=∠2,
而∠3=∠4,
∴∠EBD=∠ECD=90°,
∴BE⊥AD.
7.(1)证明:∵AC=BC,
∴∠A=∠ABC.
∵△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,
∴∠A1=∠A,A1C=AC,∠ACA1=∠BCB1=α.
∴∠A1=∠CBD,A1C=BC.
在△CBD与△CA1F中,
,
∴△CBD≌△CA1F(ASA).
(2)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
又由旋转的性质得到BC=B1C,则∠CB1B=∠CBB1,
∴∠CB1B=∠CBB1==90°﹣.
∴∠B1BD=∠CBB1﹣∠CBA=90°﹣﹣45°=45°﹣;
(3)在△CBB1中,∵CB=CB1
∴∠CBB1=∠CB1B=(180°﹣α).
又∵△ABC是等腰直角三角形,
∴∠ABC=45°.
①若B1B=B1D,则∠B1DB=∠B1BD,
∵∠B1DB=45°+α,∠B1BD=∠CBB1﹣45°=(180°﹣α)﹣45°=45°﹣,
∴45°+α=45°﹣,
∴α=0°(舍去);
②∵∠BB1C=∠B1BC>∠B1BD,
∴BD>B1D,即BD≠B1D;
③若BB1=BD,则∠BDB1=∠BB1D,即45°+α=(180°﹣α),α=30°
由①②③可知,当△BB1D为等腰三角形时,α=30°.
8.(1)证明:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CDF=∠CEB=90°,
∴∠BAD+∠B=∠FCD+∠B=90°,
∴∠BAD=∠FCD,
在△ABD和CFD中,
,
∴△ABD≌△CFD(ASA),
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
9.(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD,
∴AE=CD.
(2)∵△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠NMC=180°﹣∠BCD﹣∠CNM,∠ABC=180°﹣∠BAE﹣∠ANB,
又∠CNM=∠ANB,
∵∠ABC=90°,
∴∠NMC=90°,
∴AE⊥CD.
(3)结论:②
理由:作BK⊥AE于K,BJ⊥CD于J.
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CDB,
∴ AE BK= CD BJ,
∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,
∴BM平分∠AMD.
不妨设①成立,则△CBM≌△EBM,则AB=BD,显然不可能,故①错误.
故答案为②.
10.解:结论:AE=BD,AE⊥BD,
理由:如图,设AC交BD于N,AE交BD于O,
∵∠ACB=∠DCE=90°,∠ACD=∠ACD,
∴∠DCB=∠ECA,
在△DCB和△ECA中,
,
∴△DCB≌△ECA(SAS),
∴∠A=∠B,BD=AE
∵∠AND=∠BNC,∠B+∠BNC=90°
∴∠A+∠AND=90°,
∴∠AON=90°,
∴BD⊥AE.
11.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠CAE.
在△ADB和△AEC中,
,
∴△ADB≌AEC(SAS),
∴∠ABD=∠2=30°.
∵∠3=∠1+∠ABD.
∴∠3=25°+30°=55°.
答:∠3的度数为55°.
12.解:EC=BF,EC⊥BF.
理由:∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAE.
在△EAC和△BAF中,
∵,
∴△EAC≌△BAF(SAS),
∴EC=BF.∠AEC=∠ABF
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°,
∴∠EMB=90°,
∴EC⊥BF.
13.解:∵MS⊥PS,MN⊥SN,PQ⊥SN,
∴∠M+∠MSN=∠MSN+∠PSQ,
∴∠M=∠PSQ;
在△MNS与△SQP中,
,
∴△MNS≌△SQP(AAS).
14.证明:
∵CB⊥AD,
∴∠ABC=∠CBD=90°,
∴∠C+∠D=90°,
∵AE⊥DC,
∴∠A+∠D=90°,
∴∠A=∠C,
在△ABF和△CBD中
∴△ABF≌△CBD.
15.(1)
①解:∵在等腰三角形ABC中,∠ABC=90度,D为AC边上的中点,
∴∠C=45°,∠DBC=45°;
故答案为:45°;45°;
②证明:在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,
故BD⊥AC,
∵ED⊥DF,
∴∠BDE=∠FDC,
∴∠C=∠DBC=45°,
∴BD=DC,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(ASA);
(2)解:如图①所示:当t=0时,△PBE≌△CAE一对;
如图②所示:当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共3对;
如图③所示:当t=4时,△PBA≌△CAB一对.
16.证明:∵∠BCA=∠ECD,
∴∠BCA﹣∠ECA=∠ECD﹣∠ECA,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD.
解:图(2),图(3)中,BE和AD还相等,
理由是:如图(3)∵∠BCA=∠ECD,∠ACD+∠BCA=180°,∠ECD+∠BCE=180°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD.
17.解:(1)如图①,
∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
,
∴△ABD≌△CAF(AAS);
(2)∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(ASA);
(3)∵△ABC的面积为15,CD=2BD,
∴△ABD的面积是:×15=5,
由(2)中证出△ABE≌△CAF,
∴△ACF与△BDE的面积之和等于△ABE与△BDE的面积之和,即等于△ABD的面积,是5.
18.解:(1)PC=BC﹣BP=6﹣2t;
(2)∵t=1时,PB=2,CQ=2,
∴PC=BC﹣PB=6﹣2=4,
∵BD=AD=4,
∴PC=BD,
∵∠C=∠B,CQ=BP,
∴△QCP≌△PBD.
(3)∵点P、Q的运动速度不相等,
∴BP≠CQ,
又∵△BPD与△CPQ全等,∠B=∠C,
∴BP=PC,BD=CQ,
∴2t=6﹣2t,at=4,
解得:t=,a=.
19.证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS).
(2)BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,
∴BD=CE;
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE.
20.解:(1)EF=BE+DF,证明如下:
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为 EF=BE+DF.
(2)结论EF=BE+DF仍然成立;
理由:延长FD到点G.使DG=BE.连接AG,如图2,
在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)如图3,连接EF,延长AE、BF相交于点C,
∵∠AOB=30°+90°+(90°﹣70°)=140°,∠EOF=70°,
∴∠EOF=∠AOB,
又∵OA=OB,∠OAC+∠OBC=(90°﹣30°)+(70°+50°)=180°,
∴符合探索延伸中的条件,
∴结论EF=AE+BF成立,
即EF=2×(45+60)=210(海里).
答:此时两舰艇之间的距离是210海里.
1.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AO上运动,当AP= 时,△ABC和△PQA全等.
2.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
3.小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.6m和2m,∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由;
(2)爸爸是在距离地面多高的地方接住小明的?
4.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
5.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)求证:△ACD≌△BCD;
(2)求∠A;
(3)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(4)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
6.如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AB=3cm,则BE= cm.
(3)BE与AD有何位置关系?请说明理由.
7.如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
(1)求证:△CBD≌△CA1F;
(2)试用含α的代数式表示∠B1BD;
(3)当α等于多少度时,△BB1D是等腰三角形.
8.如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
9.如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).
10.如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,图中AE、BD有怎样的关系(数量关系和位置关系)?并证明你的结论.
11.如图AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°.求∠3的度数.
12.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.试猜想CE、BF的关系,并说明理由.
13.已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,且MS=PS.求证:△MNS≌△SQP.
14.已知:如图,CB⊥AD,AE⊥DC,垂足分别B、E,AE、BC相交于点F,且AB=BC.求证:△ABF≌△CBD.
15.在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连接BD,E、F分别是AB、BC上的点,且DE⊥DF.(1)如图1,若D为AC边上的中点.
①填空:∠C= ,∠DBC= ;
②求证:△BDE≌△CDF.
(2)如图2,D从点C出发,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤t≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.
16.如图(1),△ABC中,BC=AC,△CDE中,CE=CD,现把两个三角形的C点重合,且使∠BCA=∠ECD,连接BE,AD.求证:BE=AD.
若将△DEC绕点C旋转至图(2),(3)所示的情况时,其余条件不变,BE与AD还相等吗?利用图(3)说明理由.
17.(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
18.如图,在△ABC中,∠B=∠C,AB=8,BC=6,点D为AB的中点,点P在线段BC上以每秒2个单位的速度由点B向点C运动,同时点Q在线段CA上以每秒a个单位的速度由点C向点A运动,设运动时间为t(秒)(0≤t≤3).
(1)用含t的代数式表示线段PC的长;
(2)若点P、Q的运动速度相等,t=1时,△BPD与△CQP是否全等,请说明理由.
(3)若点P、Q的运动速度不相等,△BPD与△CQP全等时,求a的值.
19.已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.
20.(1)问题背景:
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点且∠EAF=
60°,探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
(3)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
参考答案
1.解:∵∠ACB=∠PAQ=90°,PQ=AB,
∴当AP=CB=5时,Rt△PQA≌Rt△BAC;
当AP=CA=10时,Rt△PQA≌Rt△ABC;
即AP为5或10时,△ABC和△PQA全等.
故答案为5或10.
2.解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
3.解:(1)△OBD与△COE全等.
理由如下:
由题意可知∠CEO=∠BDO=90°,OB=OC,
∵∠BOC=90°,
∴∠COE+∠BOD=∠BOD+∠OBD=90°.
∴∠COE=∠OBD,
在△COE和△OBD中,
,
∴△COE≌△OBD(AAS);
(2)∵△COE≌△OBD,
∴CE=OD,OE=BD,
∵BD、CE分别为1.6m和2m,
∴DE=OD﹣OE=CE﹣BD=2﹣1.6=0.4(m),
∵AD=1.2m,
∴AE=AD+DE=1.6(m),
答:爸爸是在距离地面1.6m的地方接住小明的.
4.(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
5.(1)证明:如图,∵D是AB的中点,
∴AD=BD.
∵在△ACD与△BCD中,,
∴△ACD≌△BCD(SSS);
(2)解:如图,∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠ABC,∠A+∠ABC=90°,
∴∠A=∠ABC=45°,即∠A=45°;
(3)证明:如图1,∵点D是AB中点,AC=BC,
∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,,
∴△AEC≌△CGB(ASA),
∴AE=CG;
(4)解:BE=CM.理由如下:
∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,,
∴△BCE≌△CAM(AAS),
∴BE=CM.
6.(1)证明:∵△ACB和△DCE都是等腰直角三角形,
∴CD=CE,CA=CB,
∵∠ACB=90°,∠DCE=90°,
∴∠ECD+∠DCB=∠DCB+∠ACB,即∠ECB=∠ACD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
(2)解:∵△ACD≌△BCE,
∴AD=BE,
∵DB=AB=3cm,
∴BE=2×3cm=6cm;
(3)解:BE与AD垂直.理由如下:
∵△ACD≌△BCE,
∴∠1=∠2,
而∠3=∠4,
∴∠EBD=∠ECD=90°,
∴BE⊥AD.
7.(1)证明:∵AC=BC,
∴∠A=∠ABC.
∵△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,
∴∠A1=∠A,A1C=AC,∠ACA1=∠BCB1=α.
∴∠A1=∠CBD,A1C=BC.
在△CBD与△CA1F中,
,
∴△CBD≌△CA1F(ASA).
(2)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
又由旋转的性质得到BC=B1C,则∠CB1B=∠CBB1,
∴∠CB1B=∠CBB1==90°﹣.
∴∠B1BD=∠CBB1﹣∠CBA=90°﹣﹣45°=45°﹣;
(3)在△CBB1中,∵CB=CB1
∴∠CBB1=∠CB1B=(180°﹣α).
又∵△ABC是等腰直角三角形,
∴∠ABC=45°.
①若B1B=B1D,则∠B1DB=∠B1BD,
∵∠B1DB=45°+α,∠B1BD=∠CBB1﹣45°=(180°﹣α)﹣45°=45°﹣,
∴45°+α=45°﹣,
∴α=0°(舍去);
②∵∠BB1C=∠B1BC>∠B1BD,
∴BD>B1D,即BD≠B1D;
③若BB1=BD,则∠BDB1=∠BB1D,即45°+α=(180°﹣α),α=30°
由①②③可知,当△BB1D为等腰三角形时,α=30°.
8.(1)证明:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CDF=∠CEB=90°,
∴∠BAD+∠B=∠FCD+∠B=90°,
∴∠BAD=∠FCD,
在△ABD和CFD中,
,
∴△ABD≌△CFD(ASA),
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
9.(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD,
∴AE=CD.
(2)∵△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠NMC=180°﹣∠BCD﹣∠CNM,∠ABC=180°﹣∠BAE﹣∠ANB,
又∠CNM=∠ANB,
∵∠ABC=90°,
∴∠NMC=90°,
∴AE⊥CD.
(3)结论:②
理由:作BK⊥AE于K,BJ⊥CD于J.
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CDB,
∴ AE BK= CD BJ,
∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,
∴BM平分∠AMD.
不妨设①成立,则△CBM≌△EBM,则AB=BD,显然不可能,故①错误.
故答案为②.
10.解:结论:AE=BD,AE⊥BD,
理由:如图,设AC交BD于N,AE交BD于O,
∵∠ACB=∠DCE=90°,∠ACD=∠ACD,
∴∠DCB=∠ECA,
在△DCB和△ECA中,
,
∴△DCB≌△ECA(SAS),
∴∠A=∠B,BD=AE
∵∠AND=∠BNC,∠B+∠BNC=90°
∴∠A+∠AND=90°,
∴∠AON=90°,
∴BD⊥AE.
11.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠CAE.
在△ADB和△AEC中,
,
∴△ADB≌AEC(SAS),
∴∠ABD=∠2=30°.
∵∠3=∠1+∠ABD.
∴∠3=25°+30°=55°.
答:∠3的度数为55°.
12.解:EC=BF,EC⊥BF.
理由:∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAE.
在△EAC和△BAF中,
∵,
∴△EAC≌△BAF(SAS),
∴EC=BF.∠AEC=∠ABF
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°,
∴∠EMB=90°,
∴EC⊥BF.
13.解:∵MS⊥PS,MN⊥SN,PQ⊥SN,
∴∠M+∠MSN=∠MSN+∠PSQ,
∴∠M=∠PSQ;
在△MNS与△SQP中,
,
∴△MNS≌△SQP(AAS).
14.证明:
∵CB⊥AD,
∴∠ABC=∠CBD=90°,
∴∠C+∠D=90°,
∵AE⊥DC,
∴∠A+∠D=90°,
∴∠A=∠C,
在△ABF和△CBD中
∴△ABF≌△CBD.
15.(1)
①解:∵在等腰三角形ABC中,∠ABC=90度,D为AC边上的中点,
∴∠C=45°,∠DBC=45°;
故答案为:45°;45°;
②证明:在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,
故BD⊥AC,
∵ED⊥DF,
∴∠BDE=∠FDC,
∴∠C=∠DBC=45°,
∴BD=DC,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(ASA);
(2)解:如图①所示:当t=0时,△PBE≌△CAE一对;
如图②所示:当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共3对;
如图③所示:当t=4时,△PBA≌△CAB一对.
16.证明:∵∠BCA=∠ECD,
∴∠BCA﹣∠ECA=∠ECD﹣∠ECA,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD.
解:图(2),图(3)中,BE和AD还相等,
理由是:如图(3)∵∠BCA=∠ECD,∠ACD+∠BCA=180°,∠ECD+∠BCE=180°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD.
17.解:(1)如图①,
∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
,
∴△ABD≌△CAF(AAS);
(2)∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(ASA);
(3)∵△ABC的面积为15,CD=2BD,
∴△ABD的面积是:×15=5,
由(2)中证出△ABE≌△CAF,
∴△ACF与△BDE的面积之和等于△ABE与△BDE的面积之和,即等于△ABD的面积,是5.
18.解:(1)PC=BC﹣BP=6﹣2t;
(2)∵t=1时,PB=2,CQ=2,
∴PC=BC﹣PB=6﹣2=4,
∵BD=AD=4,
∴PC=BD,
∵∠C=∠B,CQ=BP,
∴△QCP≌△PBD.
(3)∵点P、Q的运动速度不相等,
∴BP≠CQ,
又∵△BPD与△CPQ全等,∠B=∠C,
∴BP=PC,BD=CQ,
∴2t=6﹣2t,at=4,
解得:t=,a=.
19.证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS).
(2)BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,
∴BD=CE;
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE.
20.解:(1)EF=BE+DF,证明如下:
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为 EF=BE+DF.
(2)结论EF=BE+DF仍然成立;
理由:延长FD到点G.使DG=BE.连接AG,如图2,
在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)如图3,连接EF,延长AE、BF相交于点C,
∵∠AOB=30°+90°+(90°﹣70°)=140°,∠EOF=70°,
∴∠EOF=∠AOB,
又∵OA=OB,∠OAC+∠OBC=(90°﹣30°)+(70°+50°)=180°,
∴符合探索延伸中的条件,
∴结论EF=AE+BF成立,
即EF=2×(45+60)=210(海里).
答:此时两舰艇之间的距离是210海里.
同课章节目录
