12.2.1 利用三边判定三角形全等(SSS) 课时作业(含答案)
文档属性
| 名称 | 12.2.1 利用三边判定三角形全等(SSS) 课时作业(含答案) | 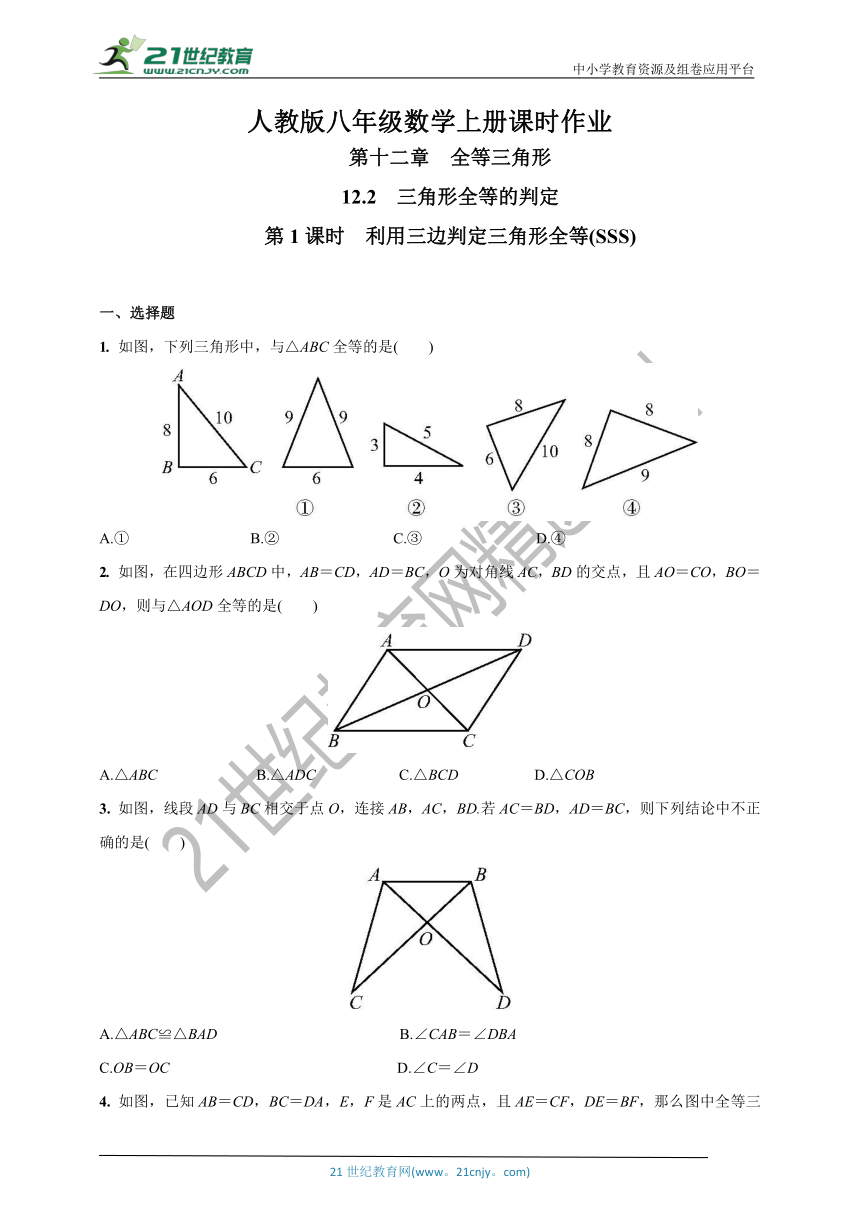 | |
| 格式 | doc | ||
| 文件大小 | 389.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 21:36:45 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上册课时作业
第十二章 全等三角形
12.2 三角形全等的判定
第1课时 利用三边判定三角形全等(SSS)
一、选择题
1. 如图,下列三角形中,与△ABC全等的是( )
A.① B.② C.③ D.④
2. 如图,在四边形ABCD中,AB=CD,AD=BC,O为对角线AC,BD的交点,且AO=CO,BO=DO,则与△AOD全等的是( )
A.△ABC B.△ADC C.△BCD D.△COB
3. 如图,线段AD与BC相交于点O,连接AB,AC,BD.若AC=BD,AD=BC,则下列结论中不正确的是( )
A.△ABC≌△BAD B.∠CAB=∠DBA
C.OB=OC D.∠C=∠D
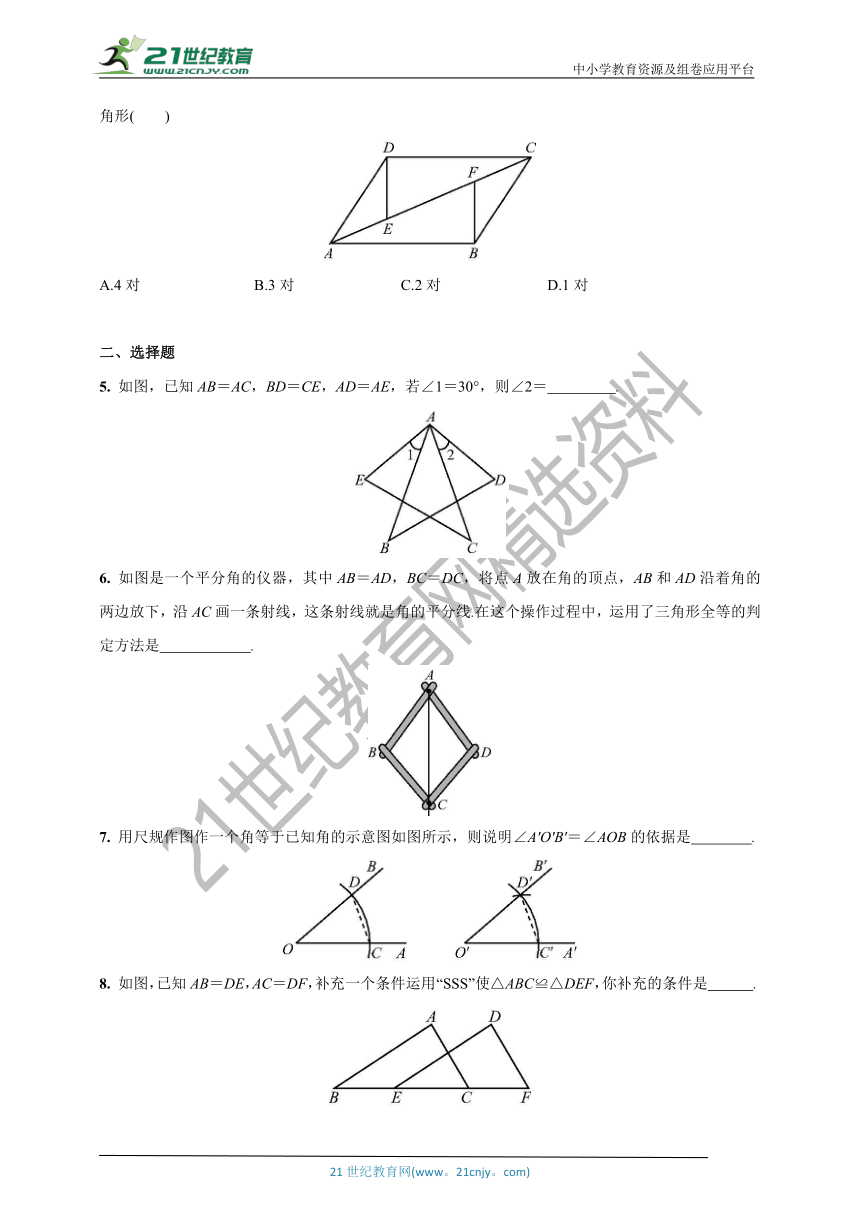
4. 如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形( )
A.4对 B.3对 C.2对 D.1对
二、选择题
5. 如图,已知AB=AC,BD=CE,AD=AE,若∠1=30°,则∠2= .
6. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线.在这个操作过程中,运用了三角形全等的判定方法是 .
7. 用尺规作图作一个角等于已知角的示意图如图所示,则说明∠A'O'B'=∠AOB的依据是 .
8. 如图,已知AB=DE,AC=DF,补充一个条件运用“SSS”使△ABC≌△DEF,你补充的条件是 .
三、解答题
9. 如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,那么AD⊥BC吗 请说明理由.
10. 如图是雨伞的截面图,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当点O沿AD滑动时,雨伞开闭.问:雨伞在开闭过程中,∠BAD与∠CAD有什么关系 为什么
11. 如图,AB⊥AC,且AB=AC,AD=AE,BD=CE.求证:AD⊥AE.
12. 如图,已知AB=AC,AD=AE,BD=CE,且B,D,E三点共线,求证:∠3=∠1+∠2.
13. 用尺规作一个角等于已知角的和(保留作图痕迹).
已知:∠1,∠2.
求作:∠AOB,使∠AOB=∠1+∠2.
14. 如图,AD=CB,E,F是AC上的两个动点,且DE=BF.
(1)若点E,F运动至如图1所示的位置,且有AF=CE,求证:△ADE≌△CBF.
(2)若点E,F运动至如图2所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗 为什么
(3)若点E,F不重合,则AD和CB平行吗 请说明理由.
参考答案
1. C 2. D 3. C 4. B
5. 30° 6. SSS 7. SSS 8. BE=CF(或BC=EF)
9. 解:AD⊥BC.理由略.
10. 解:相等. 理由:∵AE=AB,AF=AC,AB=AC,∴AE=AF. 在△AEO和△AFO中, ∴△AEO≌△AFO(SSS),∴∠BAD=∠CAD.
11. 证明:在△ABD和△ACE中, ∴△ABD≌△ACE(SSS),∴∠EAC=∠DAB,∴∠DAE=∠BAC. ∵AB⊥AC,∴∠BAC=90°,∴∠DAE=90°,即AD⊥AE.
12. 证明:易证△ABD≌△ACE,∴∠BAD=∠1,∠ABD=∠2. ∵∠3=∠BAD+∠ABD,∴∠3=∠1+∠2.
13.解:(1)作射线OA,
(2)以O为顶点作∠AOC=∠1,
(3)以点O为顶点,OC为一边,在∠AOC同侧作∠COB=∠2,则∠AOB为所求作的角.
14. 解:(1)∵AF=CE,∴AF+EF=CE+EF,即AE=CF,在△ADE和△CBF中, ∴△ADE≌△CBF(SSS).
(2)△ADE≌△CBF成立. ∵AF=CE,∴AF-EF=CE-EF,即AE=CF,在△ADE和△CBF中, ∴△ADE≌△CBF(SSS).
(3)AD与CB不一定平行. 在△ADE和△CBF中,仅有AD=CB,DE=BF不能判定它们全等,即不能得出∠A=∠C,∴AD与CB不一定平行.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
人教版八年级数学上册课时作业
第十二章 全等三角形
12.2 三角形全等的判定
第1课时 利用三边判定三角形全等(SSS)
一、选择题
1. 如图,下列三角形中,与△ABC全等的是( )
A.① B.② C.③ D.④
2. 如图,在四边形ABCD中,AB=CD,AD=BC,O为对角线AC,BD的交点,且AO=CO,BO=DO,则与△AOD全等的是( )
A.△ABC B.△ADC C.△BCD D.△COB
3. 如图,线段AD与BC相交于点O,连接AB,AC,BD.若AC=BD,AD=BC,则下列结论中不正确的是( )
A.△ABC≌△BAD B.∠CAB=∠DBA
C.OB=OC D.∠C=∠D
4. 如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形( )
A.4对 B.3对 C.2对 D.1对
二、选择题
5. 如图,已知AB=AC,BD=CE,AD=AE,若∠1=30°,则∠2= .
6. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线.在这个操作过程中,运用了三角形全等的判定方法是 .
7. 用尺规作图作一个角等于已知角的示意图如图所示,则说明∠A'O'B'=∠AOB的依据是 .
8. 如图,已知AB=DE,AC=DF,补充一个条件运用“SSS”使△ABC≌△DEF,你补充的条件是 .
三、解答题
9. 如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,那么AD⊥BC吗 请说明理由.
10. 如图是雨伞的截面图,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当点O沿AD滑动时,雨伞开闭.问:雨伞在开闭过程中,∠BAD与∠CAD有什么关系 为什么
11. 如图,AB⊥AC,且AB=AC,AD=AE,BD=CE.求证:AD⊥AE.
12. 如图,已知AB=AC,AD=AE,BD=CE,且B,D,E三点共线,求证:∠3=∠1+∠2.
13. 用尺规作一个角等于已知角的和(保留作图痕迹).
已知:∠1,∠2.
求作:∠AOB,使∠AOB=∠1+∠2.
14. 如图,AD=CB,E,F是AC上的两个动点,且DE=BF.
(1)若点E,F运动至如图1所示的位置,且有AF=CE,求证:△ADE≌△CBF.
(2)若点E,F运动至如图2所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗 为什么
(3)若点E,F不重合,则AD和CB平行吗 请说明理由.
参考答案
1. C 2. D 3. C 4. B
5. 30° 6. SSS 7. SSS 8. BE=CF(或BC=EF)
9. 解:AD⊥BC.理由略.
10. 解:相等. 理由:∵AE=AB,AF=AC,AB=AC,∴AE=AF. 在△AEO和△AFO中, ∴△AEO≌△AFO(SSS),∴∠BAD=∠CAD.
11. 证明:在△ABD和△ACE中, ∴△ABD≌△ACE(SSS),∴∠EAC=∠DAB,∴∠DAE=∠BAC. ∵AB⊥AC,∴∠BAC=90°,∴∠DAE=90°,即AD⊥AE.
12. 证明:易证△ABD≌△ACE,∴∠BAD=∠1,∠ABD=∠2. ∵∠3=∠BAD+∠ABD,∴∠3=∠1+∠2.
13.解:(1)作射线OA,
(2)以O为顶点作∠AOC=∠1,
(3)以点O为顶点,OC为一边,在∠AOC同侧作∠COB=∠2,则∠AOB为所求作的角.
14. 解:(1)∵AF=CE,∴AF+EF=CE+EF,即AE=CF,在△ADE和△CBF中, ∴△ADE≌△CBF(SSS).
(2)△ADE≌△CBF成立. ∵AF=CE,∴AF-EF=CE-EF,即AE=CF,在△ADE和△CBF中, ∴△ADE≌△CBF(SSS).
(3)AD与CB不一定平行. 在△ADE和△CBF中,仅有AD=CB,DE=BF不能判定它们全等,即不能得出∠A=∠C,∴AD与CB不一定平行.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
