12.2.2 利用两边及其夹角判定三角形全等(SAS) 课时作业(含答案)
文档属性
| 名称 | 12.2.2 利用两边及其夹角判定三角形全等(SAS) 课时作业(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 380.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上册课时作业
第十二章 全等三角形
12.2 三角形全等的判定
第2课时 利用两边及其夹角判定三角形全等(SAS)
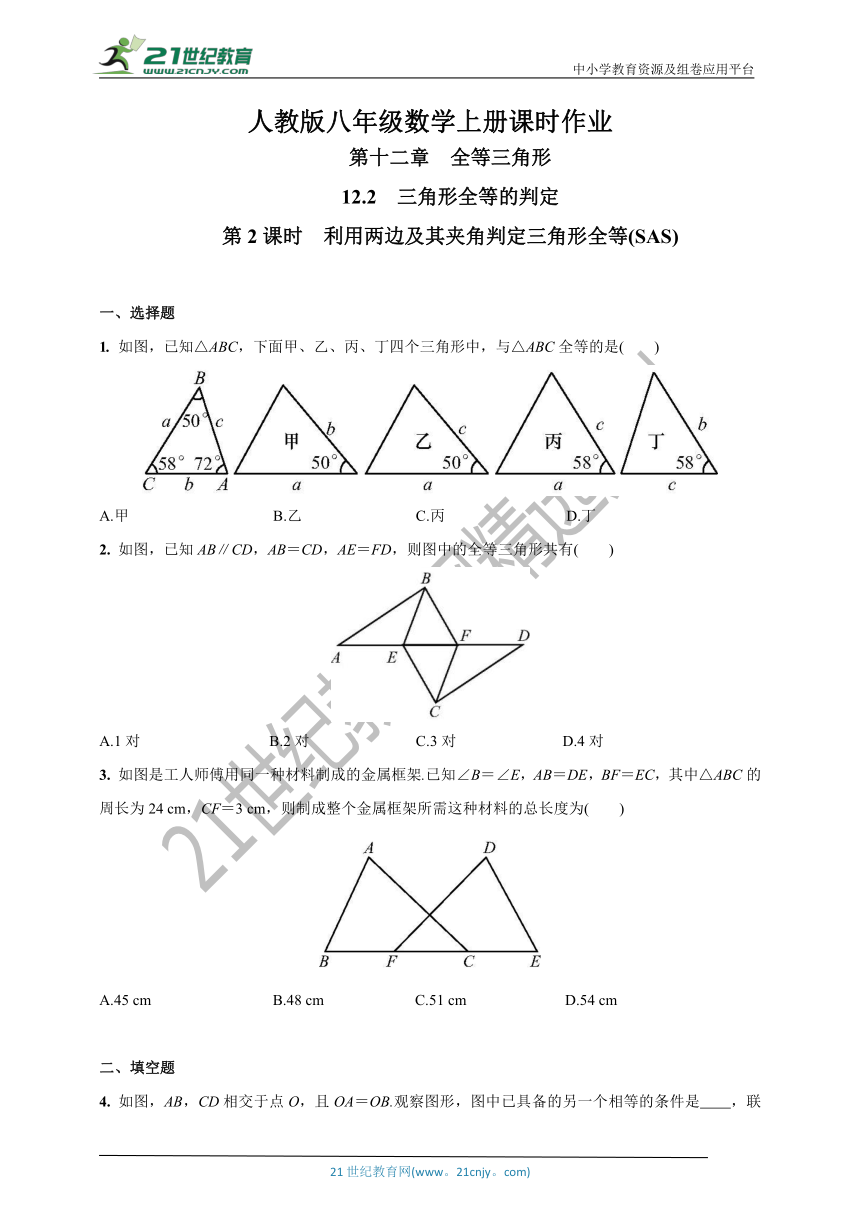
一、选择题
1. 如图,已知△ABC,下面甲、乙、丙、丁四个三角形中,与△ABC全等的是( )
A.甲 B.乙 C.丙 D.丁
2. 如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
3. 如图是工人师傅用同一种材料制成的金属框架.已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为( )
A.45 cm B.48 cm C.51 cm D.54 cm
二、填空题
4. 如图,AB,CD相交于点O,且OA=OB.观察图形,图中已具备的另一个相等的条件是 ,联想“SAS”,只需补充条件 ,则有△AOD≌△BOC.
5. 如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系为 .
6. 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,则∠C= .
7. 如图,已知AB=AC,用“SAS”定理证明△ABD≌△ACE,还需添加条件 .
8. 如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D.在AB上截取AE=AC,则△BDE的周长为 .
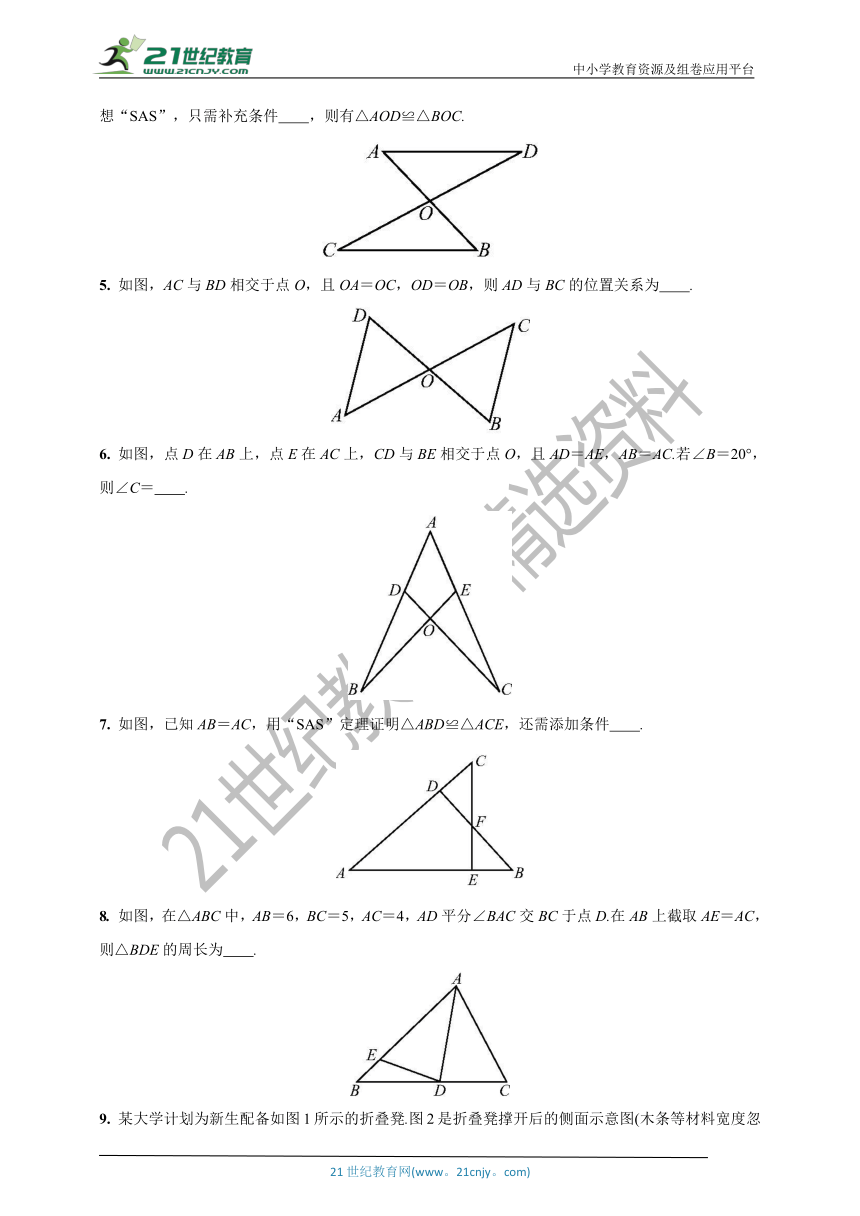
9. 某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则CB的长度为 cm.
图1 图2
三、解答题
10. 如图,点B,E,C,F在同一条直线上,AB∥DE,且AB=DE,BE=CF.求证:△ABC≌△DEF.
11. 要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD.如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD的长.你能说明其中的道理吗
12. 如图,A,F,C,D四点在同一条直线上,AF=DC,AB∥DE,且AB=DE.
(1)求证:△ABC≌△DEF;
(2)求证:∠CBF=∠FEC.
13. 如图,在△ABC中,AD是中线,求证:AD<(AB+AC).
14. 如图1,AB=8 cm,AC⊥AB,BD⊥AB,AC=BD=6 cm.点P在线段AB上以2 cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t s.
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,判断线段PC与PQ满足的关系,并说明理由.
(2)如图2,将图1中的AC⊥AB,BD⊥AB改为“∠CAB=∠DBA=α”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等 若存在,求出相应的x,t的值;若不存在,请说明理由.
图1 图2
参考答案
1. B 2. C 3. A
4. ∠AOD=∠BOC OD=OC 5. 平行 6. 20° 7. AD=AE 8. 7 9. 30
10. 证明:∵AB∥DE,∴∠B=∠DEF. ∵BE=FC,∴BC=EF. 又∵AB=DE,∴△ABC≌△DEF(SAS).
11. 解:连接AB,CD,在△ABO和△DCO中, ∴△ABO≌△DCO(SAS),∴AB
=CD.
12. 证明:(1)∵AF=DC,∴AC=DF. ∵AB∥DE,∴∠A=∠D,又∵AB=DE,∴△ABC≌△DEF(SAS).
(2)∵△ABC≌△DEF,∴BC=EF,∠ACB=∠DFE. 在△BCF和△EFC中, ∴△BCF≌△EFC(SAS),∴∠CBF=∠FEC.
13. 证明:延长AD到点E,使DE=AD,连接BE,∴AE=2AD. ∵AD是中线,∴BD=CD. 易证△ADC≌△EDB,∴AC=BE. 在△ABE中,∵AE14. 解:(1)PC⊥PQ. 理由:∵AC⊥AB,BD⊥AB,∴∠A=∠B=90°. ∵AP=BQ=2,∴BP=6,∴BP=AC,∴△ACP≌△BPQ,∴∠C=∠QPB. ∵∠APC+∠C=90°,∴∠APC+∠QPB=90°,∴∠CPQ=90°,∴PC⊥PQ.
(2)存在x的值,使得△ACP与△BPQ全等. ①若△ACP≌△BPQ,则AC=BP,AP=BQ,可得6=8-2t,2t=xt,解得x=2,t=1;②若△ACP≌△BQP,则AC=BQ,AP=BP,可得6=xt,2t=8-2t,解得x=3,t=2.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
人教版八年级数学上册课时作业
第十二章 全等三角形
12.2 三角形全等的判定
第2课时 利用两边及其夹角判定三角形全等(SAS)
一、选择题
1. 如图,已知△ABC,下面甲、乙、丙、丁四个三角形中,与△ABC全等的是( )
A.甲 B.乙 C.丙 D.丁
2. 如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
3. 如图是工人师傅用同一种材料制成的金属框架.已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为( )
A.45 cm B.48 cm C.51 cm D.54 cm
二、填空题
4. 如图,AB,CD相交于点O,且OA=OB.观察图形,图中已具备的另一个相等的条件是 ,联想“SAS”,只需补充条件 ,则有△AOD≌△BOC.
5. 如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系为 .
6. 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,则∠C= .
7. 如图,已知AB=AC,用“SAS”定理证明△ABD≌△ACE,还需添加条件 .
8. 如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D.在AB上截取AE=AC,则△BDE的周长为 .
9. 某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则CB的长度为 cm.
图1 图2
三、解答题
10. 如图,点B,E,C,F在同一条直线上,AB∥DE,且AB=DE,BE=CF.求证:△ABC≌△DEF.
11. 要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD.如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD的长.你能说明其中的道理吗
12. 如图,A,F,C,D四点在同一条直线上,AF=DC,AB∥DE,且AB=DE.
(1)求证:△ABC≌△DEF;
(2)求证:∠CBF=∠FEC.
13. 如图,在△ABC中,AD是中线,求证:AD<(AB+AC).
14. 如图1,AB=8 cm,AC⊥AB,BD⊥AB,AC=BD=6 cm.点P在线段AB上以2 cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t s.
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,判断线段PC与PQ满足的关系,并说明理由.
(2)如图2,将图1中的AC⊥AB,BD⊥AB改为“∠CAB=∠DBA=α”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等 若存在,求出相应的x,t的值;若不存在,请说明理由.
图1 图2
参考答案
1. B 2. C 3. A
4. ∠AOD=∠BOC OD=OC 5. 平行 6. 20° 7. AD=AE 8. 7 9. 30
10. 证明:∵AB∥DE,∴∠B=∠DEF. ∵BE=FC,∴BC=EF. 又∵AB=DE,∴△ABC≌△DEF(SAS).
11. 解:连接AB,CD,在△ABO和△DCO中, ∴△ABO≌△DCO(SAS),∴AB
=CD.
12. 证明:(1)∵AF=DC,∴AC=DF. ∵AB∥DE,∴∠A=∠D,又∵AB=DE,∴△ABC≌△DEF(SAS).
(2)∵△ABC≌△DEF,∴BC=EF,∠ACB=∠DFE. 在△BCF和△EFC中, ∴△BCF≌△EFC(SAS),∴∠CBF=∠FEC.
13. 证明:延长AD到点E,使DE=AD,连接BE,∴AE=2AD. ∵AD是中线,∴BD=CD. 易证△ADC≌△EDB,∴AC=BE. 在△ABE中,∵AE
(2)存在x的值,使得△ACP与△BPQ全等. ①若△ACP≌△BPQ,则AC=BP,AP=BQ,可得6=8-2t,2t=xt,解得x=2,t=1;②若△ACP≌△BQP,则AC=BQ,AP=BP,可得6=xt,2t=8-2t,解得x=3,t=2.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
