第03讲 正方形的性质与判定(考点讲解)(含答案)
文档属性
| 名称 | 第03讲 正方形的性质与判定(考点讲解)(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第03讲 正方形的性质与判定
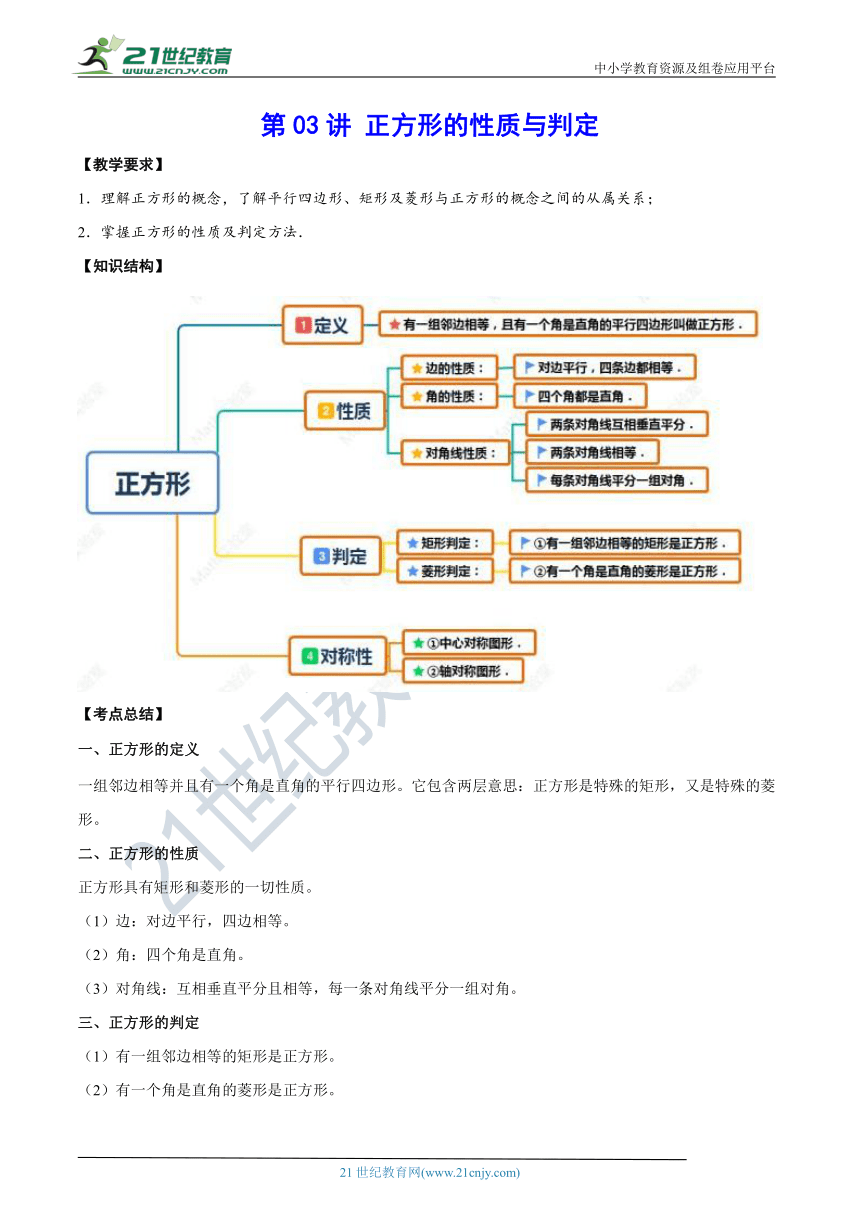
【教学要求】
1.理解正方形的概念,了解平行四边形、矩形及菱形与正方形的概念之间的从属关系;
2.掌握正方形的性质及判定方法.
【知识结构】
( http: / / www.21cnjy.com / )
【考点总结】
一、正方形的定义
一组邻边相等并且有一个角是直角的平行四边形。它包含两层意思:正方形是特殊的矩形,又是特殊的菱形。
二、正方形的性质
正方形具有矩形和菱形的一切性质。
(1)边:对边平行,四边相等。
(2)角:四个角是直角。
(3)对角线:互相垂直平分且相等,每一条对角线平分一组对角。
三、正方形的判定
(1)有一组邻边相等的矩形是正方形。
(2)有一个角是直角的菱形是正方形。
(3)对角线互相垂直平分且相等的四边形是正方形。
(4)有一组邻边相等且有一个角是直角的平行四边形是正方形。
【例题讲解】
【类型】一、 正方形的定义与性质
例1、如图所示,正方形ABCD的对 ( http: / / www.21cnjy.com )角线相交于点O,点E是BC上任意一点,EG⊥BD于G,EF⊥AC于F,若AC=10,则EG+EF的值为( )21cnjy.com
( http: / / www.21cnjy.com / )
A.10 B.4 C.8 D.5
【解析】D
根据ABCD是正方形,求得△BEG,△CEF是等腰直角三角形,即可求得结果.
∵ABCD是正方形,AC,BD是对角线,
∴∠OBC=∠OCB=45°,
∵EG⊥BD,EF⊥AC,
∴△BEG,△CEF是等腰直角三角形.
∴CF=EF.
∵AC⊥BD,
∴EFOG是矩形.
∴EG=FO.
∴EF+EG=CF+FO=CO=5,
故选D.
【总结与反思】本题考查了正方形的性质,等腰直角三角形的性质.
【训练】已知:如图,E为正方形ABCD的边BC延长线上的点,F是CD边上一点,且
CE=CF,连接DE,BF.求证:DE=BF.
( http: / / www.21cnjy.com / )
证明:∵四边形ABCD是正方形,
∴BC=DC,∠BCD=90°
∵E为BC延长线上的点,
∴∠DCE=90°,
∴∠BCD=∠DCE.
在△BCF和△DCE中,
( http: / / www.21cnjy.com / ),
∴△BCF≌△DCE(SAS),
∴BF=DE.
【训练】如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
( http: / / www.21cnjy.com / )
A.75° B.60° C.55° D.45°21世纪教育网版权所有
【答案】B;
提示:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
【类型】二、正方形中的旋转问题
例2、在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG.21·cn·jy·com
( http: / / www.21cnjy.com / )
(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.www.21-cn-jy.com
(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.2·1·c·n·j·y
【解析】(1) EG=CG,EG⊥CG.
(2)EG=CG,EG⊥CG.
证明:延长FE交DC延长线于M,连MG.
∵∠AEM=90°,∠EBC=90°,∠BCM=90°,
∴四边形BEMC是矩形.
∴BE=CM,∠EMC=90°,
又∵BE=EF,
∴EF=CM.
∵∠EMC=90°,FG=DG,
∴MG= QUOTE FD=FG.
∵BC=EM,BC=CD,
∴EM=CD.
∵EF=CM,
∴FM=DM,
∴∠F=45°.
又FG=DG,
∠CMG= QUOTE ∠EMC=45°,
∴∠F=∠GMC.
∴△GFE≌△GMC.
∴EG=CG,∠FGE=∠MGC.
∵∠FMC=90°,MF=MD,FG=DG,
∴MG⊥FD,
∴∠FGE+∠EGM=90°,
∴∠MGC+∠EGM=90°,
即∠EGC=90°,
∴EG⊥CG.
( http: / / www.21cnjy.com / )
【总结与反思】 此题是对正方形性质结合旋转的性质的考察,在正方形的题型中占有重要的地位.
【类型】三、正方形的性质与判定
例3、如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.【来源:21·世纪·教育·网】
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
( http: / / www.21cnjy.com / )
【解析】 证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
【总结与反思】根据正方形的性质及判定定理即可顺利解答此题..
【训练】如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.21教育网
(1)求证:四边形CDOF是矩形;
(2)当∠AOC多少度时,四边形CDOF是正方形?并说明理由.
( http: / / www.21cnjy.com / )
(1)证明:∵OD平分∠AOC,OF平分∠COB(已知),
∴∠AOC=2∠COD,∠COB=2∠COF,
∵∠AOC+∠BOC=180°,
∴2∠COD+2∠COF=180°,
∴∠COD+∠COF=90°,
∴∠DOF=90°;
∵OA=OC,OD平分∠AOC(已知),
∴OD⊥AC,AD=DC(等腰三角形的“三线合一”的性质),
∴∠CDO=90°,
∵CF⊥OF,
∴∠CFO=90°
∴四边形CDOF是矩形;
(2)当∠AOC=90°时,四边形CDOF是正方形;理由如下:
∵∠AOC=90°,AD=DC,
∴OD=DC;
又由(1)知四边形CDOF是矩形,则
四边形CDOF是正方形;
因此,当∠AOC=90°时,四边形CDOF是正方形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第03讲 正方形的性质与判定
【教学要求】
1.理解正方形的概念,了解平行四边形、矩形及菱形与正方形的概念之间的从属关系;
2.掌握正方形的性质及判定方法.
【知识结构】
( http: / / www.21cnjy.com / )
【考点总结】
一、正方形的定义
一组邻边相等并且有一个角是直角的平行四边形。它包含两层意思:正方形是特殊的矩形,又是特殊的菱形。
二、正方形的性质
正方形具有矩形和菱形的一切性质。
(1)边:对边平行,四边相等。
(2)角:四个角是直角。
(3)对角线:互相垂直平分且相等,每一条对角线平分一组对角。
三、正方形的判定
(1)有一组邻边相等的矩形是正方形。
(2)有一个角是直角的菱形是正方形。
(3)对角线互相垂直平分且相等的四边形是正方形。
(4)有一组邻边相等且有一个角是直角的平行四边形是正方形。
【例题讲解】
【类型】一、 正方形的定义与性质
例1、如图所示,正方形ABCD的对 ( http: / / www.21cnjy.com )角线相交于点O,点E是BC上任意一点,EG⊥BD于G,EF⊥AC于F,若AC=10,则EG+EF的值为( )21cnjy.com
( http: / / www.21cnjy.com / )
A.10 B.4 C.8 D.5
【解析】D
根据ABCD是正方形,求得△BEG,△CEF是等腰直角三角形,即可求得结果.
∵ABCD是正方形,AC,BD是对角线,
∴∠OBC=∠OCB=45°,
∵EG⊥BD,EF⊥AC,
∴△BEG,△CEF是等腰直角三角形.
∴CF=EF.
∵AC⊥BD,
∴EFOG是矩形.
∴EG=FO.
∴EF+EG=CF+FO=CO=5,
故选D.
【总结与反思】本题考查了正方形的性质,等腰直角三角形的性质.
【训练】已知:如图,E为正方形ABCD的边BC延长线上的点,F是CD边上一点,且
CE=CF,连接DE,BF.求证:DE=BF.
( http: / / www.21cnjy.com / )
证明:∵四边形ABCD是正方形,
∴BC=DC,∠BCD=90°
∵E为BC延长线上的点,
∴∠DCE=90°,
∴∠BCD=∠DCE.
在△BCF和△DCE中,
( http: / / www.21cnjy.com / ),
∴△BCF≌△DCE(SAS),
∴BF=DE.
【训练】如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
( http: / / www.21cnjy.com / )
A.75° B.60° C.55° D.45°21世纪教育网版权所有
【答案】B;
提示:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
【类型】二、正方形中的旋转问题
例2、在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG.21·cn·jy·com
( http: / / www.21cnjy.com / )
(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.www.21-cn-jy.com
(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.2·1·c·n·j·y
【解析】(1) EG=CG,EG⊥CG.
(2)EG=CG,EG⊥CG.
证明:延长FE交DC延长线于M,连MG.
∵∠AEM=90°,∠EBC=90°,∠BCM=90°,
∴四边形BEMC是矩形.
∴BE=CM,∠EMC=90°,
又∵BE=EF,
∴EF=CM.
∵∠EMC=90°,FG=DG,
∴MG= QUOTE FD=FG.
∵BC=EM,BC=CD,
∴EM=CD.
∵EF=CM,
∴FM=DM,
∴∠F=45°.
又FG=DG,
∠CMG= QUOTE ∠EMC=45°,
∴∠F=∠GMC.
∴△GFE≌△GMC.
∴EG=CG,∠FGE=∠MGC.
∵∠FMC=90°,MF=MD,FG=DG,
∴MG⊥FD,
∴∠FGE+∠EGM=90°,
∴∠MGC+∠EGM=90°,
即∠EGC=90°,
∴EG⊥CG.
( http: / / www.21cnjy.com / )
【总结与反思】 此题是对正方形性质结合旋转的性质的考察,在正方形的题型中占有重要的地位.
【类型】三、正方形的性质与判定
例3、如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.【来源:21·世纪·教育·网】
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
( http: / / www.21cnjy.com / )
【解析】 证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
【总结与反思】根据正方形的性质及判定定理即可顺利解答此题..
【训练】如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.21教育网
(1)求证:四边形CDOF是矩形;
(2)当∠AOC多少度时,四边形CDOF是正方形?并说明理由.
( http: / / www.21cnjy.com / )
(1)证明:∵OD平分∠AOC,OF平分∠COB(已知),
∴∠AOC=2∠COD,∠COB=2∠COF,
∵∠AOC+∠BOC=180°,
∴2∠COD+2∠COF=180°,
∴∠COD+∠COF=90°,
∴∠DOF=90°;
∵OA=OC,OD平分∠AOC(已知),
∴OD⊥AC,AD=DC(等腰三角形的“三线合一”的性质),
∴∠CDO=90°,
∵CF⊥OF,
∴∠CFO=90°
∴四边形CDOF是矩形;
(2)当∠AOC=90°时,四边形CDOF是正方形;理由如下:
∵∠AOC=90°,AD=DC,
∴OD=DC;
又由(1)知四边形CDOF是矩形,则
四边形CDOF是正方形;
因此,当∠AOC=90°时,四边形CDOF是正方形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
