12.2.3 利用两角一边判定三角形全等(ASA,AAS) 课时作业(含答案)
文档属性
| 名称 | 12.2.3 利用两角一边判定三角形全等(ASA,AAS) 课时作业(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 372.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 21:34:05 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上册课时作业
第十二章 全等三角形
12.2 三角形全等的判定
第3课时 利用两角一边判定三角形全等(ASA,AAS)
一、选择题
1. 如图,已知∠1=∠2,则不一定能使△ABC≌△ABD的条件是( )
A.AC=AD B.BC=BD C.∠C=∠D D.∠3=∠4
2. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
3. 在△ABC和△A'B'C'中:①AB=A'B';②BC=B'C';③AC=A'C';④∠A=∠A';⑤∠B=∠B';⑥∠C=∠C'.则下列条件组合中,不能保证△ABC≌△A'B'C'的是( )
A.①②③ B.①②⑤ C.②④⑤ D.①③⑤
二、填空题
4. 如图,线段AB,CD相交于点O,AO=BO.若用“ASA”判定△AOC≌△BOD,还需要添加的一个条件是 .
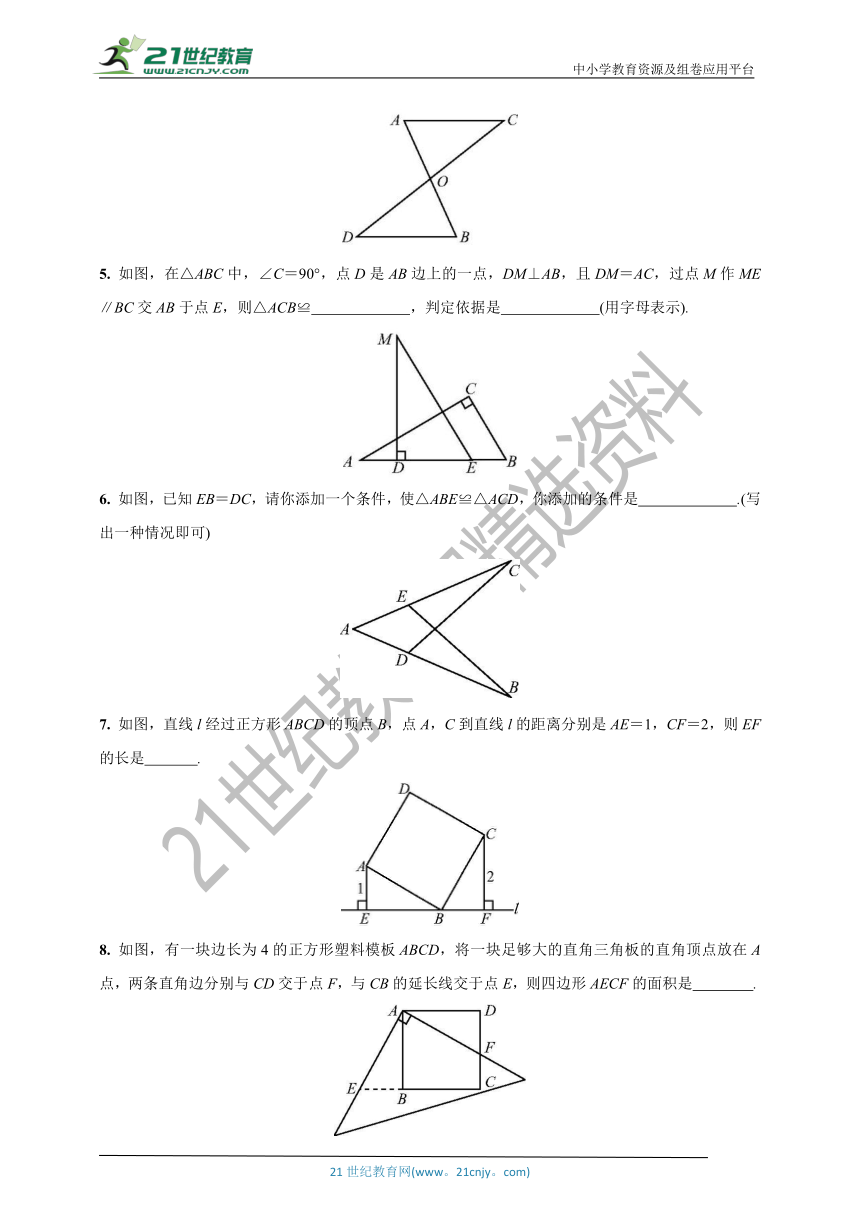
5. 如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,则△ACB≌ ,判定依据是 (用字母表示).
6. 如图,已知EB=DC,请你添加一个条件,使△ABE≌△ACD,你添加的条件是 .(写出一种情况即可)
7. 如图,直线l经过正方形ABCD的顶点B,点A,C到直线l的距离分别是AE=1,CF=2,则EF的长是 .
8. 如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点放在A点,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 .
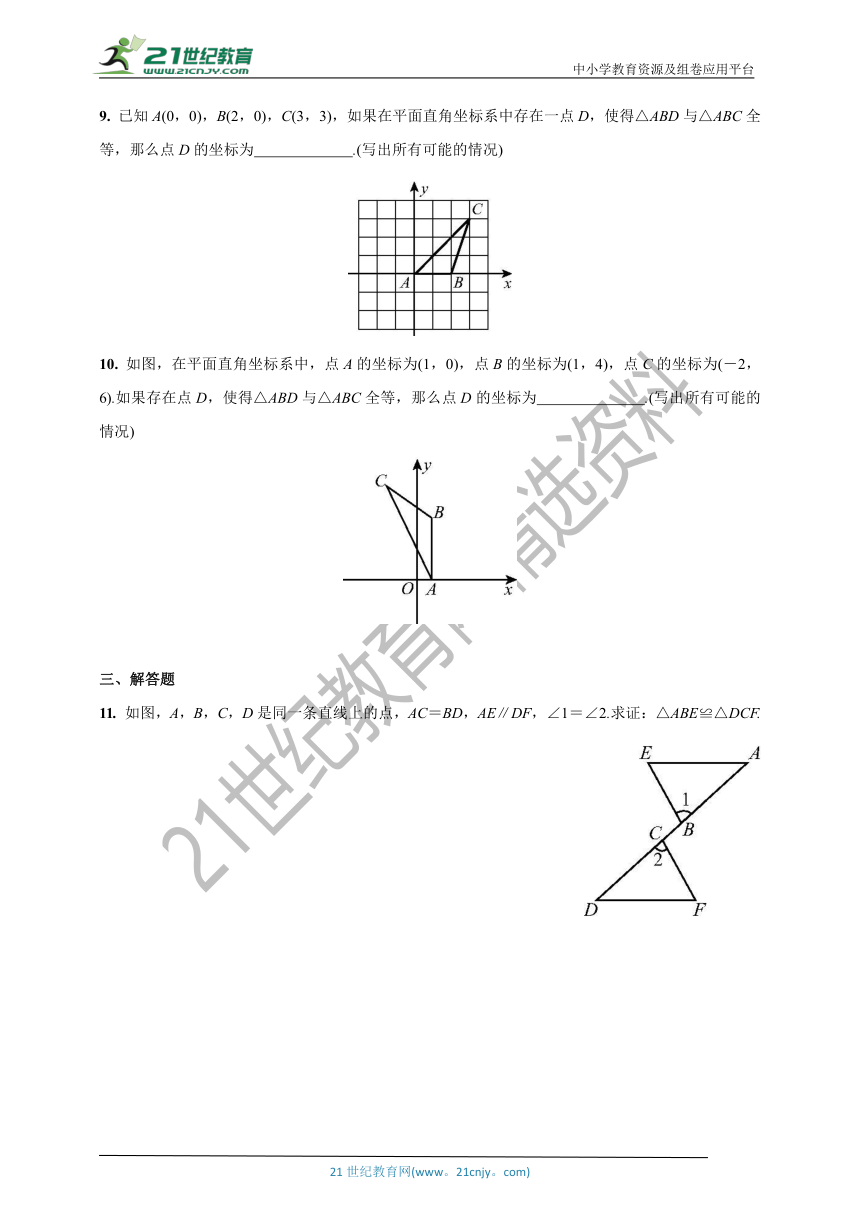
9. 已知A(0,0),B(2,0),C(3,3),如果在平面直角坐标系中存在一点D,使得△ABD与△ABC全等,那么点D的坐标为 .(写出所有可能的情况)
10. 如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(1,4),点C的坐标为(-2,6).如果存在点D,使得△ABD与△ABC全等,那么点D的坐标为 .(写出所有可能的情况)
三、解答题
11. 如图,A,B,C,D是同一条直线上的点,AC=BD,AE∥DF,∠1=∠2.求证:△ABE≌△DCF.
12. 如图,点D在△ABC外部,点C在DE边上,BC与AD相交于点O.若∠1=∠2=∠3,AC=AE,求证:△ABC≌△ADE.
13. 如图,一条河流MN旁边有两个村庄A,B,AD⊥MN于点D.由于有山峰阻挡,村庄B到河边MN的距离不能直接测量,河边恰好有一个地点C能到达A,B两个村庄,与A,B的连线夹角为90°,且与A,B的距离也相等,测量C,D的距离为150 m,请求出村庄B到河边的距离.
14. 如图,已知AD∥CB且AD=CB,O是BD的中点,过点O作直线分别交BA的延长线于点E,交DC的延长线于点F,与AD,BC分别相交于点M,N.
(1)图中共有 对全等三角形.
(2)试说明:△EBO≌△FDO.
15. 如图1,在△ABC中,AD=BD,H是高AD和BE的交点.
(1)求证:BH=AC.
(2)如图2,当∠BAC为钝角时,其他条件不变,此时结论BH=AC还成立吗 若成立,请证明;若不成立,请说明理由.
图1 图2
参考答案
1. B 2. C 3. D
4. ∠A=∠B(答案不唯一) 5. △MDE AAS(答案不唯一) 6. ∠AEB=∠ADC(答案不唯一) 7. 3 8. 16 9. (3,-3)或(-1,3)或(-1,-3) 10. (4,6)或(-2,-2)或(4,-2)
11. 证明:∵AE∥DF,∴∠A=∠D. ∵AC=BD,∴AB=CD. 在△ABE和△DCF中, ∴△ABE≌△DCF(ASA).
12. 证明:∵∠1=∠3,∴∠BAC=∠DAE. ∵∠B=∠180°-∠1-∠AOB,∠D=180°-∠2-∠COD,且∠2=∠1,∠AOB=∠COD,∴∠B=∠D. 在△ABC和△ADE中, ∴△ABC≌△ADE(AAS).
13. 解:过点B作BE⊥MN于点E. ∵∠ADC=∠ACB=90°,∴∠A=∠BCE. 在△ADC和△CEB中, ∴△ADC≌△CEB(AAS),∴BE=CD=150 m,即村庄B到河边的距离是150 m.
14. 解:(1)5
(2)∵AD∥BC,∴∠ADB=∠CBD,又∵AD=BC,BD=BD,∴△ABD≌△CDB(SAS),∴∠ABD=∠CDB. ∵O是BD的中点,∴OB=OD. 在△EBO和△FDO中, ∴△EBO≌△FDO(ASA).
15. 解:(1)∵AD⊥BC,BE⊥AC,∴∠ADC=90°,∠BEC=90°,∴∠DAC+∠C=90°,∠EBC+∠C=90°,∴∠DAC=∠EBC.易证△BDH≌△ADC,∴BH=AC.
(2)BH=AC仍然成立. 理由:∵AD⊥BC,BE⊥AC,∴∠ADB=∠AEB=90°,∴∠CBE+∠C=90°,∠CBE+∠DHB=90°,∴∠DHB=∠C. 在△BDH和△ADC中, ∴△BDH≌△ADC( AAS ),∴BH=AC.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
人教版八年级数学上册课时作业
第十二章 全等三角形
12.2 三角形全等的判定
第3课时 利用两角一边判定三角形全等(ASA,AAS)
一、选择题
1. 如图,已知∠1=∠2,则不一定能使△ABC≌△ABD的条件是( )
A.AC=AD B.BC=BD C.∠C=∠D D.∠3=∠4
2. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
3. 在△ABC和△A'B'C'中:①AB=A'B';②BC=B'C';③AC=A'C';④∠A=∠A';⑤∠B=∠B';⑥∠C=∠C'.则下列条件组合中,不能保证△ABC≌△A'B'C'的是( )
A.①②③ B.①②⑤ C.②④⑤ D.①③⑤
二、填空题
4. 如图,线段AB,CD相交于点O,AO=BO.若用“ASA”判定△AOC≌△BOD,还需要添加的一个条件是 .
5. 如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,则△ACB≌ ,判定依据是 (用字母表示).
6. 如图,已知EB=DC,请你添加一个条件,使△ABE≌△ACD,你添加的条件是 .(写出一种情况即可)
7. 如图,直线l经过正方形ABCD的顶点B,点A,C到直线l的距离分别是AE=1,CF=2,则EF的长是 .
8. 如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点放在A点,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 .
9. 已知A(0,0),B(2,0),C(3,3),如果在平面直角坐标系中存在一点D,使得△ABD与△ABC全等,那么点D的坐标为 .(写出所有可能的情况)
10. 如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(1,4),点C的坐标为(-2,6).如果存在点D,使得△ABD与△ABC全等,那么点D的坐标为 .(写出所有可能的情况)
三、解答题
11. 如图,A,B,C,D是同一条直线上的点,AC=BD,AE∥DF,∠1=∠2.求证:△ABE≌△DCF.
12. 如图,点D在△ABC外部,点C在DE边上,BC与AD相交于点O.若∠1=∠2=∠3,AC=AE,求证:△ABC≌△ADE.
13. 如图,一条河流MN旁边有两个村庄A,B,AD⊥MN于点D.由于有山峰阻挡,村庄B到河边MN的距离不能直接测量,河边恰好有一个地点C能到达A,B两个村庄,与A,B的连线夹角为90°,且与A,B的距离也相等,测量C,D的距离为150 m,请求出村庄B到河边的距离.
14. 如图,已知AD∥CB且AD=CB,O是BD的中点,过点O作直线分别交BA的延长线于点E,交DC的延长线于点F,与AD,BC分别相交于点M,N.
(1)图中共有 对全等三角形.
(2)试说明:△EBO≌△FDO.
15. 如图1,在△ABC中,AD=BD,H是高AD和BE的交点.
(1)求证:BH=AC.
(2)如图2,当∠BAC为钝角时,其他条件不变,此时结论BH=AC还成立吗 若成立,请证明;若不成立,请说明理由.
图1 图2
参考答案
1. B 2. C 3. D
4. ∠A=∠B(答案不唯一) 5. △MDE AAS(答案不唯一) 6. ∠AEB=∠ADC(答案不唯一) 7. 3 8. 16 9. (3,-3)或(-1,3)或(-1,-3) 10. (4,6)或(-2,-2)或(4,-2)
11. 证明:∵AE∥DF,∴∠A=∠D. ∵AC=BD,∴AB=CD. 在△ABE和△DCF中, ∴△ABE≌△DCF(ASA).
12. 证明:∵∠1=∠3,∴∠BAC=∠DAE. ∵∠B=∠180°-∠1-∠AOB,∠D=180°-∠2-∠COD,且∠2=∠1,∠AOB=∠COD,∴∠B=∠D. 在△ABC和△ADE中, ∴△ABC≌△ADE(AAS).
13. 解:过点B作BE⊥MN于点E. ∵∠ADC=∠ACB=90°,∴∠A=∠BCE. 在△ADC和△CEB中, ∴△ADC≌△CEB(AAS),∴BE=CD=150 m,即村庄B到河边的距离是150 m.
14. 解:(1)5
(2)∵AD∥BC,∴∠ADB=∠CBD,又∵AD=BC,BD=BD,∴△ABD≌△CDB(SAS),∴∠ABD=∠CDB. ∵O是BD的中点,∴OB=OD. 在△EBO和△FDO中, ∴△EBO≌△FDO(ASA).
15. 解:(1)∵AD⊥BC,BE⊥AC,∴∠ADC=90°,∠BEC=90°,∴∠DAC+∠C=90°,∠EBC+∠C=90°,∴∠DAC=∠EBC.易证△BDH≌△ADC,∴BH=AC.
(2)BH=AC仍然成立. 理由:∵AD⊥BC,BE⊥AC,∴∠ADB=∠AEB=90°,∴∠CBE+∠C=90°,∠CBE+∠DHB=90°,∴∠DHB=∠C. 在△BDH和△ADC中, ∴△BDH≌△ADC( AAS ),∴BH=AC.
21世纪教育网 www。21cnjy。com精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www。21cnjy。com)
