山东省东营区实验学校鲁教版(五四制) 2021-2022学年七年级上学期第一次月考考试数学试题(word版含答案)
文档属性
| 名称 | 山东省东营区实验学校鲁教版(五四制) 2021-2022学年七年级上学期第一次月考考试数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 505.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 17:36:33 | ||
图片预览

文档简介
七年级上册月考达标测试
(考试时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列体育运动标志中,从图案看不是轴对称图形的有( )
A.4个 B.3个 C.2个 D.1个
2.已知三角形两边的长分别是4和0,则此三角形第三边的长可能是( )
A.5
B.6
C.11
D.16
3.如图,在△ABC中,AD⊥B,AE平分∠BAC,∠B=40°,∠C=60°,则∠DAE的度数为( )
A.40°
B.30°
C.20°
D.10°
4.如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E,F,则图中与∠C(∠C除外)相等的角有( )
A.3个
B.4个
C.5个
D.6个
5.如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若
∠O=50°,∠D=35°,则∠OBC等于( )
A.70°
B.80°
C.85°
D.95°
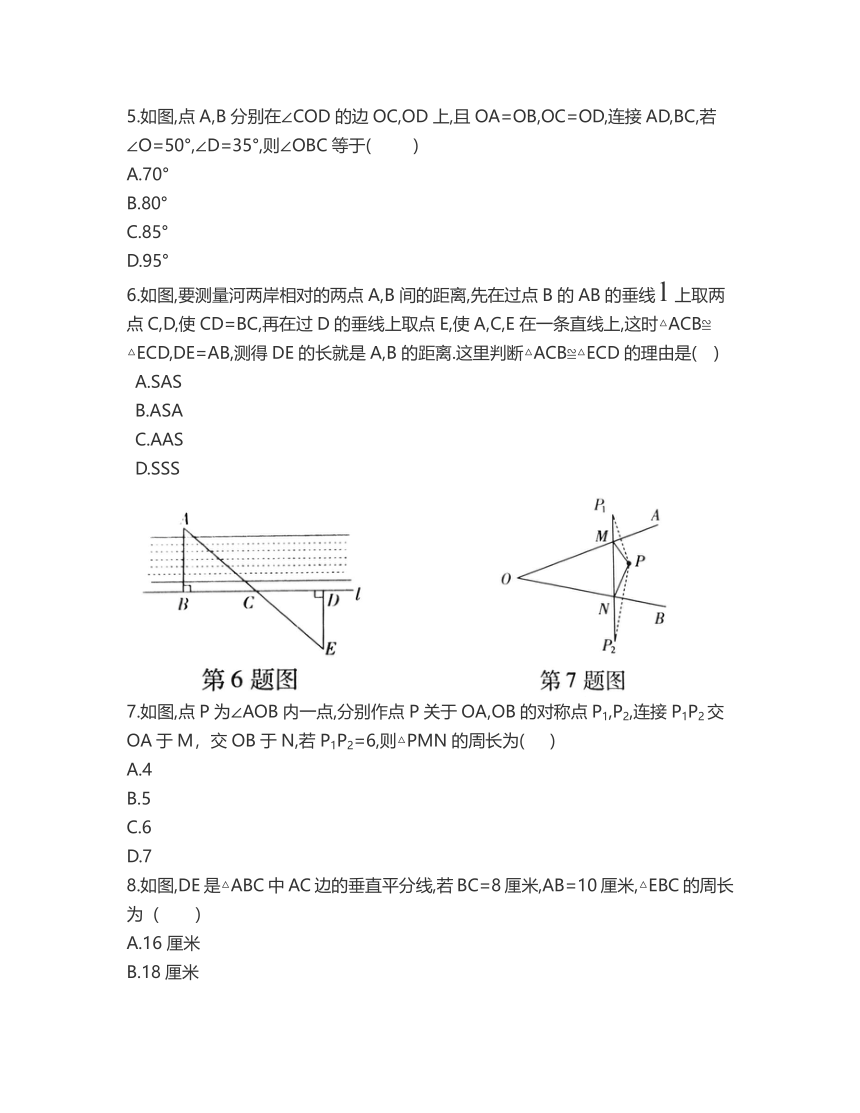
6.如图,要测量河两岸相对的两点A,B间的距离,先在过点B的AB的垂线l上取两点C,D,使CD=BC,再在过D的垂线上取点E,使A,C,E在一条直线上,这时△ACB≌
△ECD,DE=AB,测得DE的长就是A,B的距离.这里判断△ACB≌△ECD的理由是( )
A.SAS
B.ASA
C.AAS
D.SSS
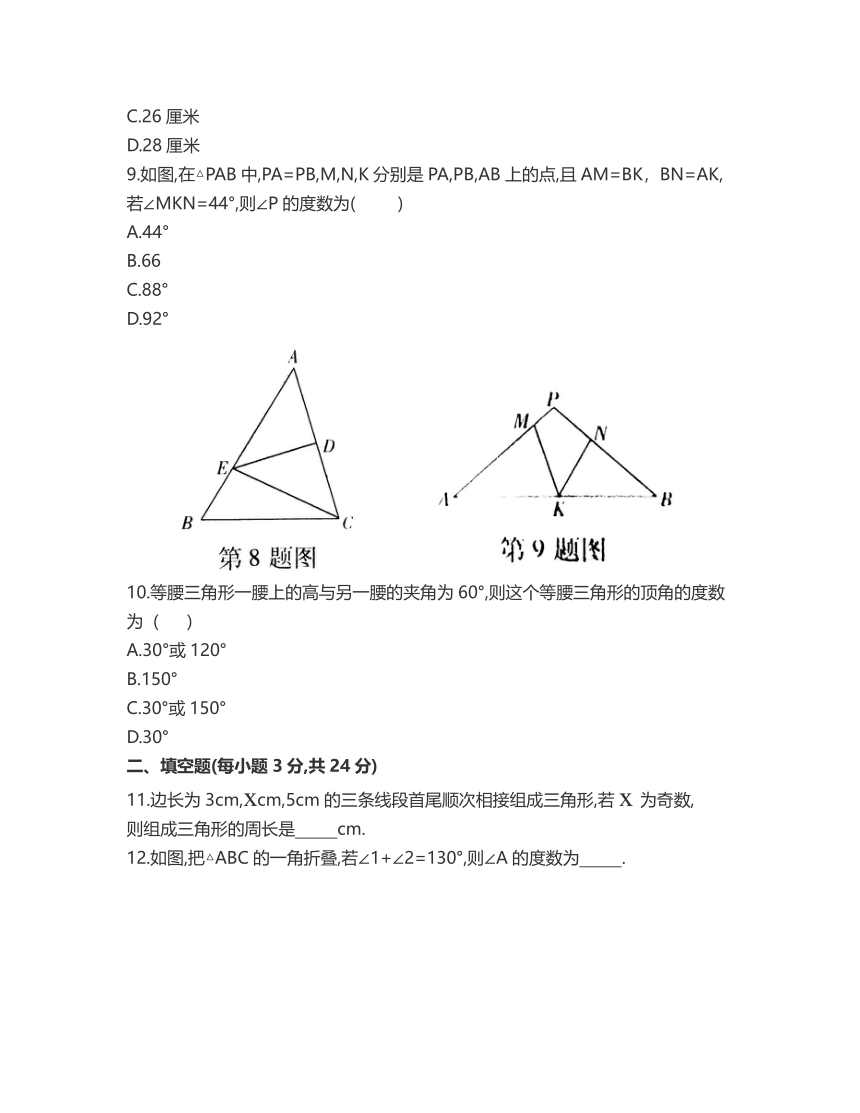
7.如图,点P为∠AOB内一点,分别作点P关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为( )
A.4
B.5
C.6
D.7
8.如图,DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,△EBC的周长为( )
A.16厘米
B.18厘米
C.26厘米
D.28厘米
9.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66
C.88°
D.92°
10.等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角的度数为( )
A.30°或120°
B.150°
C.30°或150°
D.30°
二、填空题(每小题3分,共24分)
11.边长为3cm,xcm,5cm的三条线段首尾顺次相接组成三角形,若x为奇数,
则组成三角形的周长是 cm.
12.如图,把△ABC的一角折叠,若∠1+∠2=130°,则∠A的度数为 .
13.已知△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=4,则AC= .
14.如图,已知AD=BC,根据“SSS”需要一个条件 ,可证明△ABC≌△BAD;根据“SAS”,还需要一个条件 ,可证明△ABC≌△BAD.
15.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,
DE=1.7cm,则BE= .
16.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有 个.
17.如图,在△ABC中∠C=90°,AM是∠CAB的平分线,CM=20cm,那么M到AB的距离为 cm.
18.如图,△ABC中,BC=7,AB的垂直平分线分别交AB,BC于点D、E,AC的垂直平分线分别交AC,BC于点F,G,则△AEG的周长为 .
三、解答题(共66分)
19.(6分)如图,AD是△ABC的外角平分线,交BC的延长线于点D,若∠B=30°,
∠DAE=55°,求∠ACD的度数
20.(8分)如图,已知点A,F,E,C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
21.(8分)如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.
求证:AE=FB
22.(10分)如图,AB⊥BC,DC⊥BC,AE=DE,AB=EC.求证:BC=AB+DC.
23.(10分)在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB,BC于D、E.若
∠CAB=∠B+30°,求∠AEB.
24.(12分)在平面直角坐标系中描出点A(-2,0),B(3,1),C(2,3),将各点用线段依次连接起来,并解答如下问题:
(1)在平面直角坐标系中画出△A B C ,使它与△ABC关于x轴对称,并直接写出△A B C 三个顶点的坐标;
(2)求△ABC的面积.
25.(12分)如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,
OE∥AC
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD,DE,EC三者有什么关系 写出你的判断过程.
1.B 2.C 3.D 4.A 5.D 6.B 7C 8.B 9.D 10.C
11.11或13或15 12.65° 13.5 14.BD=AC(不唯一) ∠DAB=∠CBA(不唯一) 15.0.8cm 16.4 17.20 18.7
19.解:∵∠DAE=55°,AD平分∠CAE,
∴∠CAE=110°
∵∠CAE是△ABC的外角,∠B=30°
∴∠ACB=110°-30°=80°,
∴∠ACD=180°-80°=100°
20.(1)△ABE≌△CDF,△AFD≌△CEB.
(2)证明:∵AB∥CD,
∴∠1=∠2.
∵AF=CE
∴AF+EF=CE+EF,
即AE=FC
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS)
21.证明:∵CE∥DF
∴∠ACE=∠D
在△ACE和△FDB中,
∴△ACE≌△FDB(SAS)
∴AE=FB
22.证明:∵AB⊥BC,DC⊥BC
∴∠B=∠C=90°
在Rt△ABE和Rt△ECD中,
∴Rt△AEB≌Rt△ECD(HL)
∴DC=BE
∵BC=BE+CE
∴BC=AB+DC
23.解:∵DE垂直平分斜边AB
∴AE=BE
∴∠EAB=∠EBA
∵∠CAB=∠B+30°,∠CAB=∠CAE+∠EAB
∴∠CAE=30°
∵∠C=90°
∴∠AEC=60°,
∴∠AEB=120°
24.解:(1)如图所示,由图可知A'(-2,0),B'(3,-1),C'(2,-3)
(2)由图可知,S△ABC=5×3-×5×1-×3×4-×2×1
=15--6-1=5.5
25.解:(1)△ODE是等边三角形,其理由是:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°
∵OD∥AB,OE∥AC
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°,
∴△ODE是等边三角形
(2)BD=DE=EC,其理由是BO平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°
∵OD∥AB
∴∠BOD=∠ABO=30°,∴∠DBO=∠DOB
∴DB=DO
同理,EC=EO.∵DE=OD=OE,
∴BD=DE=EC
(考试时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列体育运动标志中,从图案看不是轴对称图形的有( )
A.4个 B.3个 C.2个 D.1个
2.已知三角形两边的长分别是4和0,则此三角形第三边的长可能是( )
A.5
B.6
C.11
D.16
3.如图,在△ABC中,AD⊥B,AE平分∠BAC,∠B=40°,∠C=60°,则∠DAE的度数为( )
A.40°
B.30°
C.20°
D.10°
4.如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E,F,则图中与∠C(∠C除外)相等的角有( )
A.3个
B.4个
C.5个
D.6个
5.如图,点A,B分别在∠COD的边OC,OD上,且OA=OB,OC=OD,连接AD,BC,若
∠O=50°,∠D=35°,则∠OBC等于( )
A.70°
B.80°
C.85°
D.95°
6.如图,要测量河两岸相对的两点A,B间的距离,先在过点B的AB的垂线l上取两点C,D,使CD=BC,再在过D的垂线上取点E,使A,C,E在一条直线上,这时△ACB≌
△ECD,DE=AB,测得DE的长就是A,B的距离.这里判断△ACB≌△ECD的理由是( )
A.SAS
B.ASA
C.AAS
D.SSS
7.如图,点P为∠AOB内一点,分别作点P关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为( )
A.4
B.5
C.6
D.7
8.如图,DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,△EBC的周长为( )
A.16厘米
B.18厘米
C.26厘米
D.28厘米
9.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66
C.88°
D.92°
10.等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角的度数为( )
A.30°或120°
B.150°
C.30°或150°
D.30°
二、填空题(每小题3分,共24分)
11.边长为3cm,xcm,5cm的三条线段首尾顺次相接组成三角形,若x为奇数,
则组成三角形的周长是 cm.
12.如图,把△ABC的一角折叠,若∠1+∠2=130°,则∠A的度数为 .
13.已知△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=4,则AC= .
14.如图,已知AD=BC,根据“SSS”需要一个条件 ,可证明△ABC≌△BAD;根据“SAS”,还需要一个条件 ,可证明△ABC≌△BAD.
15.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,
DE=1.7cm,则BE= .
16.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有 个.
17.如图,在△ABC中∠C=90°,AM是∠CAB的平分线,CM=20cm,那么M到AB的距离为 cm.
18.如图,△ABC中,BC=7,AB的垂直平分线分别交AB,BC于点D、E,AC的垂直平分线分别交AC,BC于点F,G,则△AEG的周长为 .
三、解答题(共66分)
19.(6分)如图,AD是△ABC的外角平分线,交BC的延长线于点D,若∠B=30°,
∠DAE=55°,求∠ACD的度数
20.(8分)如图,已知点A,F,E,C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
21.(8分)如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.
求证:AE=FB
22.(10分)如图,AB⊥BC,DC⊥BC,AE=DE,AB=EC.求证:BC=AB+DC.
23.(10分)在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB,BC于D、E.若
∠CAB=∠B+30°,求∠AEB.
24.(12分)在平面直角坐标系中描出点A(-2,0),B(3,1),C(2,3),将各点用线段依次连接起来,并解答如下问题:
(1)在平面直角坐标系中画出△A B C ,使它与△ABC关于x轴对称,并直接写出△A B C 三个顶点的坐标;
(2)求△ABC的面积.
25.(12分)如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,
OE∥AC
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD,DE,EC三者有什么关系 写出你的判断过程.
1.B 2.C 3.D 4.A 5.D 6.B 7C 8.B 9.D 10.C
11.11或13或15 12.65° 13.5 14.BD=AC(不唯一) ∠DAB=∠CBA(不唯一) 15.0.8cm 16.4 17.20 18.7
19.解:∵∠DAE=55°,AD平分∠CAE,
∴∠CAE=110°
∵∠CAE是△ABC的外角,∠B=30°
∴∠ACB=110°-30°=80°,
∴∠ACD=180°-80°=100°
20.(1)△ABE≌△CDF,△AFD≌△CEB.
(2)证明:∵AB∥CD,
∴∠1=∠2.
∵AF=CE
∴AF+EF=CE+EF,
即AE=FC
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS)
21.证明:∵CE∥DF
∴∠ACE=∠D
在△ACE和△FDB中,
∴△ACE≌△FDB(SAS)
∴AE=FB
22.证明:∵AB⊥BC,DC⊥BC
∴∠B=∠C=90°
在Rt△ABE和Rt△ECD中,
∴Rt△AEB≌Rt△ECD(HL)
∴DC=BE
∵BC=BE+CE
∴BC=AB+DC
23.解:∵DE垂直平分斜边AB
∴AE=BE
∴∠EAB=∠EBA
∵∠CAB=∠B+30°,∠CAB=∠CAE+∠EAB
∴∠CAE=30°
∵∠C=90°
∴∠AEC=60°,
∴∠AEB=120°
24.解:(1)如图所示,由图可知A'(-2,0),B'(3,-1),C'(2,-3)
(2)由图可知,S△ABC=5×3-×5×1-×3×4-×2×1
=15--6-1=5.5
25.解:(1)△ODE是等边三角形,其理由是:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°
∵OD∥AB,OE∥AC
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°,
∴△ODE是等边三角形
(2)BD=DE=EC,其理由是BO平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°
∵OD∥AB
∴∠BOD=∠ABO=30°,∴∠DBO=∠DOB
∴DB=DO
同理,EC=EO.∵DE=OD=OE,
∴BD=DE=EC
同课章节目录
