3.3幂函数 课件(共21张PPT)
文档属性
| 名称 | 3.3幂函数 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 21.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 11:53:40 | ||
图片预览





文档简介
(共21张PPT)
3.3幂函数
人教A(2019)版
必修一
新知导入
我们来考察日常生活中的几个问题
1、如果张红以1元/kg的价格购习了某种蔬菜w千克,那么她需要付的钱数p是多少元?
p=w
这里的p是w的函数
2、如果正方形的边长为a,那么正方形的面积是S是多少?
S=a2
这里的S是a的函数
3、如果立方体的边长为b,那么立方体的体积是V是多少?
V=b3
这里的V是b的函数
4、如果正方形场地的面积为S,那么正方形的边长c是多少?
c=
这里的c是S的函数
5、如果某人t s内骑车行进了1km,那么他骑车的平均速度v是多少?
v=t-1
这里的V是t的函数
考察这些函数,它们有什么共同特征?
都是幂,且底数为自变量指数为常数的函数。
新知讲解
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
幂函数的基本特征:
注:(1) 为常量, .
(2) 中前面的系数为1.
试一试:哪些是幂函数?
①
②
③
④
⑤
(3)底数只能是自变量x,而不能是其它含x的形式。
√
√
⑥ y=x3+2
一、幂函数的概念
新知讲解
通常可以先根据函数解析式求出函数的定义域,画出函数的
图象;再利用图和解析式,讨论函数的值域、单调性、奇偶性等
问题。
研究一个函数,我们利用哪些手段来分析研究它呢?
新知讲解
二、幂函数的图像及性质
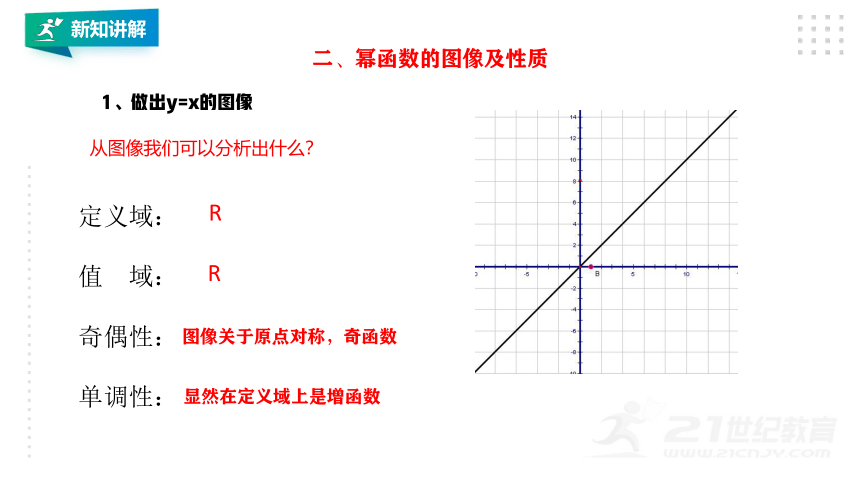
1、做出y=x的图像
从图像我们可以分析出什么?
定义域:
值 域:
奇偶性:
单调性:
R
R
图像关于原点对称,奇函数
显然在定义域上是增函数
新知讲解
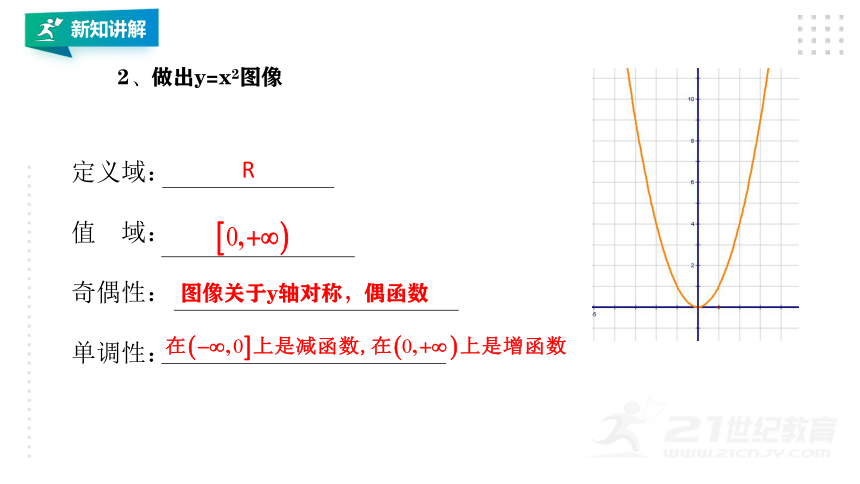
2、做出y=x2图像
定义域:
值 域:
奇偶性:
单调性:
R
图像关于y轴对称,偶函数
新知讲解
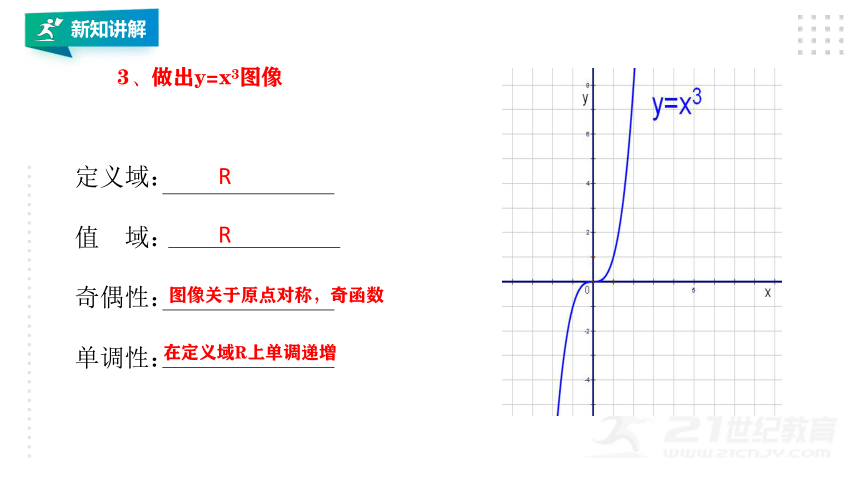
3、做出y=x3图像
定义域:
值 域:
奇偶性:
单调性:
R
R
图像关于原点对称,奇函数
在定义域R上单调递增
4、做出 图像
定义域:
值 域:
奇偶性:
单调性:
即不关于y轴对称,也不关于原点对称,
非奇非偶函数
新知讲解
新知讲解
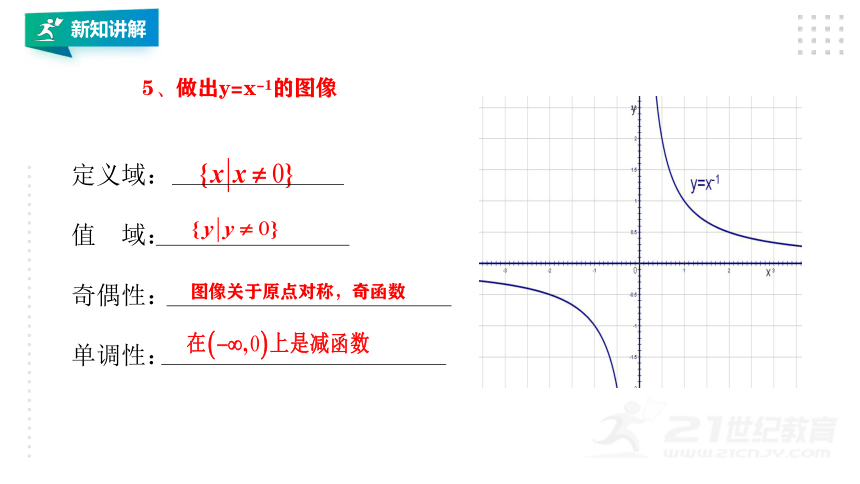
5、做出y=x-1的图像
定义域:
值 域:
奇偶性:
单调性:
图像关于原点对称,奇函数
新知讲解
6、在同一坐标系画出上述函数图像,观察它们的共同特征
1
1
x
y
0
y=x
y=x2
y=x3
y=x-1
(1) 图像都过点(1,1);
(4) 在第一象限内,y=x-1的图像向坐标轴无限接近。
性质
定义域
值域
奇偶性
单调性
定点
我们总结出幂函数的性质
奇
增
偶
在 减
在 增
增
增
奇
非奇非偶
奇
在 减
在 减
合作探究
证明:
函数的定义域是[0,+∞)
例1.函数f(x)=(m2-m-1)xm2+m-3是幂函数,且当x∈(0,+∞)时,f(x)是
增函数,求f(x)的解析式.
合作探究
解:根据幂函数定义得
m2-m-1=1,解得m=2或m=-1,
当m=2时,f(x)=x3在(0,+∞)上是增函数,
当m=-1时,f(x)=x-3在(0,+∞)上是减函数,
不合要求.
∴f(x)的解析式为f(x)=x3.
合作探究
例2.利用幂函数的图像和性质,比较下列各组值的大小:
增函数
合作探究
课堂练习
1. 下列函数为幂函数的是( )
A.y=2x3 B.y=2x2-1 C.y=x-1 D.y=3x2
2.幂函数y=f(x)的图象经过点(3,√3),则f(x)( )
A.是偶函数,且在(0,+∞)上是增函数 B.是偶函数,且在(0,+∞)上是减函数
C.是奇函数,且在(0,+∞)上是减函数
D.既不是奇函数,也不是偶函数,且在(0,+∞)上是增函数
3.幂函数的图象过点(2, ),则它的单调递增区间是( )
A.(0,+∞) B.[0,+∞) C.(-∞,+∞) D.(-∞,0)
4.若 ,则a的取值范围是
1
4
(-1, )
3
2
课堂总结
一、幂函数的定义:
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
性质
定义域
值域
奇偶性 奇 偶 奇 非奇非偶 奇
单调性 增 在 增 增 增 在 减
在 减 在 减
定点
二、我们总结出幂函数的性质
板书设计
利用幂函数的单调性判别大小.
幂函数的定义;
幂函数的性质;
幂函数
一般地,函数 叫做幂函数,其中x是
自变量,a是常数.
(1) 图像都过点(1,1);
作业布置
2、课本P91 练习题1、2、3
复习巩固 第1、3题
1、 比较下列各题中两个值的大小
(1)
0.50.2 ( )1
(3)
(2)
( )
( )
(4)
( )
https://www.21cnjy.com/help/help_extract.php
3.3幂函数
人教A(2019)版
必修一
新知导入
我们来考察日常生活中的几个问题
1、如果张红以1元/kg的价格购习了某种蔬菜w千克,那么她需要付的钱数p是多少元?
p=w
这里的p是w的函数
2、如果正方形的边长为a,那么正方形的面积是S是多少?
S=a2
这里的S是a的函数
3、如果立方体的边长为b,那么立方体的体积是V是多少?
V=b3
这里的V是b的函数
4、如果正方形场地的面积为S,那么正方形的边长c是多少?
c=
这里的c是S的函数
5、如果某人t s内骑车行进了1km,那么他骑车的平均速度v是多少?
v=t-1
这里的V是t的函数
考察这些函数,它们有什么共同特征?
都是幂,且底数为自变量指数为常数的函数。
新知讲解
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
幂函数的基本特征:
注:(1) 为常量, .
(2) 中前面的系数为1.
试一试:哪些是幂函数?
①
②
③
④
⑤
(3)底数只能是自变量x,而不能是其它含x的形式。
√
√
⑥ y=x3+2
一、幂函数的概念
新知讲解
通常可以先根据函数解析式求出函数的定义域,画出函数的
图象;再利用图和解析式,讨论函数的值域、单调性、奇偶性等
问题。
研究一个函数,我们利用哪些手段来分析研究它呢?
新知讲解
二、幂函数的图像及性质
1、做出y=x的图像
从图像我们可以分析出什么?
定义域:
值 域:
奇偶性:
单调性:
R
R
图像关于原点对称,奇函数
显然在定义域上是增函数
新知讲解
2、做出y=x2图像
定义域:
值 域:
奇偶性:
单调性:
R
图像关于y轴对称,偶函数
新知讲解
3、做出y=x3图像
定义域:
值 域:
奇偶性:
单调性:
R
R
图像关于原点对称,奇函数
在定义域R上单调递增
4、做出 图像
定义域:
值 域:
奇偶性:
单调性:
即不关于y轴对称,也不关于原点对称,
非奇非偶函数
新知讲解
新知讲解
5、做出y=x-1的图像
定义域:
值 域:
奇偶性:
单调性:
图像关于原点对称,奇函数
新知讲解
6、在同一坐标系画出上述函数图像,观察它们的共同特征
1
1
x
y
0
y=x
y=x2
y=x3
y=x-1
(1) 图像都过点(1,1);
(4) 在第一象限内,y=x-1的图像向坐标轴无限接近。
性质
定义域
值域
奇偶性
单调性
定点
我们总结出幂函数的性质
奇
增
偶
在 减
在 增
增
增
奇
非奇非偶
奇
在 减
在 减
合作探究
证明:
函数的定义域是[0,+∞)
例1.函数f(x)=(m2-m-1)xm2+m-3是幂函数,且当x∈(0,+∞)时,f(x)是
增函数,求f(x)的解析式.
合作探究
解:根据幂函数定义得
m2-m-1=1,解得m=2或m=-1,
当m=2时,f(x)=x3在(0,+∞)上是增函数,
当m=-1时,f(x)=x-3在(0,+∞)上是减函数,
不合要求.
∴f(x)的解析式为f(x)=x3.
合作探究
例2.利用幂函数的图像和性质,比较下列各组值的大小:
增函数
合作探究
课堂练习
1. 下列函数为幂函数的是( )
A.y=2x3 B.y=2x2-1 C.y=x-1 D.y=3x2
2.幂函数y=f(x)的图象经过点(3,√3),则f(x)( )
A.是偶函数,且在(0,+∞)上是增函数 B.是偶函数,且在(0,+∞)上是减函数
C.是奇函数,且在(0,+∞)上是减函数
D.既不是奇函数,也不是偶函数,且在(0,+∞)上是增函数
3.幂函数的图象过点(2, ),则它的单调递增区间是( )
A.(0,+∞) B.[0,+∞) C.(-∞,+∞) D.(-∞,0)
4.若 ,则a的取值范围是
1
4
(-1, )
3
2
课堂总结
一、幂函数的定义:
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
性质
定义域
值域
奇偶性 奇 偶 奇 非奇非偶 奇
单调性 增 在 增 增 增 在 减
在 减 在 减
定点
二、我们总结出幂函数的性质
板书设计
利用幂函数的单调性判别大小.
幂函数的定义;
幂函数的性质;
幂函数
一般地,函数 叫做幂函数,其中x是
自变量,a是常数.
(1) 图像都过点(1,1);
作业布置
2、课本P91 练习题1、2、3
复习巩固 第1、3题
1、 比较下列各题中两个值的大小
(1)
0.50.2 ( )1
(3)
(2)
( )
( )
(4)
( )
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
