人教版数学选修1-1第一章1.1.3四种命题的相互关系课件
文档属性
| 名称 | 人教版数学选修1-1第一章1.1.3四种命题的相互关系课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 100.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-06 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
复习:
1)可以判断真假的陈述句称为命题.
2)其中判断为真的语句称为真命题,
判断为假的语句称为假命题.
可写成 “若 p, 则 q” 的形式
或 “如果p,那么q” 的形式
或 “只要p,就有q” 的形式
命题都是由条件和结论两部分构成
2、互否命题:如果第一个命题的条件和结论是第二个命题的条件和结论的否定,那么这两个命题叫做互否命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的否命题。
3、互为逆否命题:如果第一个命题的条件和结论分别是第二个命题的结论的否定和条件的否定,那么这两个命题叫做互为逆否命题。
1、互逆命题:如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫互逆命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题。
三个概念
若p 则q
逆否命题:
原命题:
逆命题:
否命题:
若q 则p
若 p 则 q
若 q 则 p
观察与思考
?
你能说出其中任意两个命题之间的关系吗
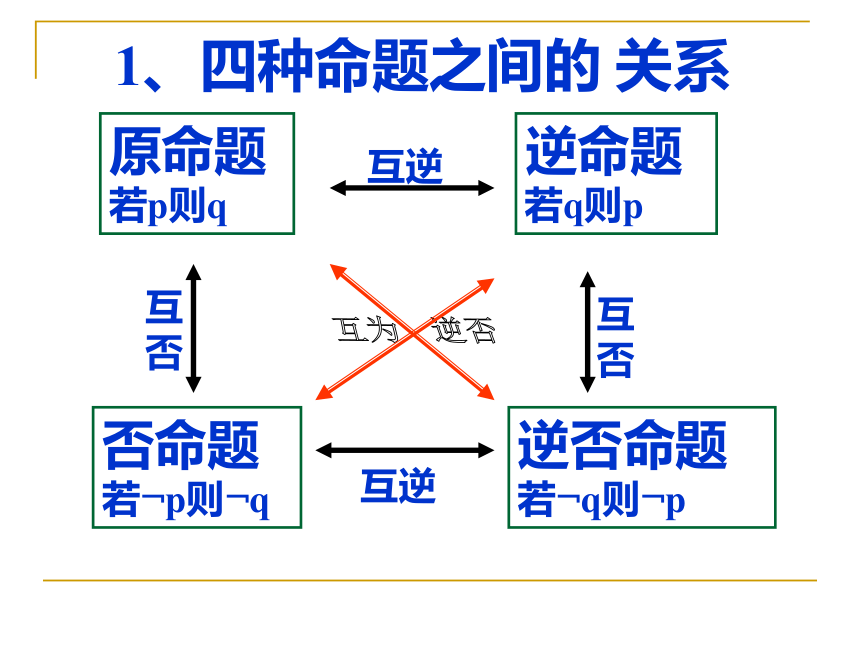
1、四种命题之间的 关系
原命题
若p则q
逆命题
若q则p
否命题
若﹁p则﹁q
逆否命题
若﹁q则﹁p
互逆
互否
互否
互逆
2)原命题:若a=0, 则ab=0。
逆命题:若ab=0, 则a=0。
否命题:若a≠ 0, 则ab≠0。
逆否命题:若ab≠0,则a≠0。
(真)
(假)
(假)
(真)
(真)
2.四种命题的真假
看下面的例子:
1)原命题:若x=2或x=3, 则x2-5x+6=0。
逆命题:若x2-5x+6=0, 则x=2或x=3。
否命题:若x≠2且x≠3, 则x2-5x+6≠0 。
逆否命题:若x2-5x+6≠0,则x≠2且x≠3。
(真)
(真)
(真)
3) 原命题:若a > b, 则 ac2>bc2。
逆命题:若ac2>bc2,则a>b。
否命题:若a≤b,则ac2≤bc2。
逆否命题:若ac2≤bc2,则a≤b。
(假)
(真)
(真)
(假)
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
一般地,四种命题的真假性,有而且仅有下面四种情况:
想一想?
(2) 若其逆命题为真,则其否命题一定为真。但其原命题、逆否命题不一定为真。
由以上三例及总结我们能发现什么?
即(1)原命题与逆否命题同真假。
原命题的逆命题与否命题同真假。
(1) 原命题为真,则其逆否命题一定为真。但其逆命题、否命题不一定为真。
总结:
(两个命题为互逆命题或互否命题,它们的真假性没有关系).
练一练
1.判断下列说法是否正确。
1)一个命题的逆命题为真,它的逆否命题不一定为真;
(对)
2)一个命题的否命题为真,它的逆命题一定为真。
(对)
3)一个命题的原命题为假,它的逆命题一定为假。
(错)
4)一个命题的逆否命题为假,它的否命题为假。
(错)
如:原命题:若A∪B=A, 则A∩B=φ。
逆命题:若A∩B=φ,则A∪B=A。
否命题:若A∪B≠A,则A∩B≠φ。
逆否命题:若A∩B≠φ,则A∪B≠A。
(假)
(假)
(假)
(假)
2.四种命题真假的个数可能为( )个。
答:0个、2个、4个。
例题讲解
例1:设原命题是:当c>0时,若a>b,
则ac>bc. 写出它的逆命题、否命题、逆否命题。并分别判断它们的真假。
解:逆命题:当c>0时,若ac>bc, 则a>b.
否命题:当c>0时,若a≤b, 则ac≤bc.
逆否命题:当c>0时,若ac≤bc, 则a≤b.
(真)
(真)
(真)
分析:“当c>0时”是大前提,写其它命题时应该保留。
原命题的条件是“a>b”,
结论是“ac>bc”。
例2 若m≤0或n≤0,则m+n≤0。写出其逆命题、否命题、逆否命题,并分别指出其真假。
分析:搞清四种命题的定义及其关系,注意“且” “或”的
否定为“或” “且”。
解:逆命题:若m+n≤0,则m≤0或n≤0。
否命题:若m>0且n>0, 则m+n>0.
逆否命题:若m+n>0, 则m>0且n>0.
(真)
(真)
(假)
小结:在判断四种命题的真假时,只需判断两种命题的真假。因为逆命题与否命题真假等价,逆否命题与原命题真假等价。
巩固练习:P8练习
例3:证明x2+y2=0,则x=y=0.
小结: 1、本节内容: (1)四种命题的关系
(2)四种命题的真假关系
(3) 一种思想
复习:
1)可以判断真假的陈述句称为命题.
2)其中判断为真的语句称为真命题,
判断为假的语句称为假命题.
可写成 “若 p, 则 q” 的形式
或 “如果p,那么q” 的形式
或 “只要p,就有q” 的形式
命题都是由条件和结论两部分构成
2、互否命题:如果第一个命题的条件和结论是第二个命题的条件和结论的否定,那么这两个命题叫做互否命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的否命题。
3、互为逆否命题:如果第一个命题的条件和结论分别是第二个命题的结论的否定和条件的否定,那么这两个命题叫做互为逆否命题。
1、互逆命题:如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫互逆命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题。
三个概念
若p 则q
逆否命题:
原命题:
逆命题:
否命题:
若q 则p
若 p 则 q
若 q 则 p
观察与思考
?
你能说出其中任意两个命题之间的关系吗
1、四种命题之间的 关系
原命题
若p则q
逆命题
若q则p
否命题
若﹁p则﹁q
逆否命题
若﹁q则﹁p
互逆
互否
互否
互逆
2)原命题:若a=0, 则ab=0。
逆命题:若ab=0, 则a=0。
否命题:若a≠ 0, 则ab≠0。
逆否命题:若ab≠0,则a≠0。
(真)
(假)
(假)
(真)
(真)
2.四种命题的真假
看下面的例子:
1)原命题:若x=2或x=3, 则x2-5x+6=0。
逆命题:若x2-5x+6=0, 则x=2或x=3。
否命题:若x≠2且x≠3, 则x2-5x+6≠0 。
逆否命题:若x2-5x+6≠0,则x≠2且x≠3。
(真)
(真)
(真)
3) 原命题:若a > b, 则 ac2>bc2。
逆命题:若ac2>bc2,则a>b。
否命题:若a≤b,则ac2≤bc2。
逆否命题:若ac2≤bc2,则a≤b。
(假)
(真)
(真)
(假)
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
一般地,四种命题的真假性,有而且仅有下面四种情况:
想一想?
(2) 若其逆命题为真,则其否命题一定为真。但其原命题、逆否命题不一定为真。
由以上三例及总结我们能发现什么?
即(1)原命题与逆否命题同真假。
原命题的逆命题与否命题同真假。
(1) 原命题为真,则其逆否命题一定为真。但其逆命题、否命题不一定为真。
总结:
(两个命题为互逆命题或互否命题,它们的真假性没有关系).
练一练
1.判断下列说法是否正确。
1)一个命题的逆命题为真,它的逆否命题不一定为真;
(对)
2)一个命题的否命题为真,它的逆命题一定为真。
(对)
3)一个命题的原命题为假,它的逆命题一定为假。
(错)
4)一个命题的逆否命题为假,它的否命题为假。
(错)
如:原命题:若A∪B=A, 则A∩B=φ。
逆命题:若A∩B=φ,则A∪B=A。
否命题:若A∪B≠A,则A∩B≠φ。
逆否命题:若A∩B≠φ,则A∪B≠A。
(假)
(假)
(假)
(假)
2.四种命题真假的个数可能为( )个。
答:0个、2个、4个。
例题讲解
例1:设原命题是:当c>0时,若a>b,
则ac>bc. 写出它的逆命题、否命题、逆否命题。并分别判断它们的真假。
解:逆命题:当c>0时,若ac>bc, 则a>b.
否命题:当c>0时,若a≤b, 则ac≤bc.
逆否命题:当c>0时,若ac≤bc, 则a≤b.
(真)
(真)
(真)
分析:“当c>0时”是大前提,写其它命题时应该保留。
原命题的条件是“a>b”,
结论是“ac>bc”。
例2 若m≤0或n≤0,则m+n≤0。写出其逆命题、否命题、逆否命题,并分别指出其真假。
分析:搞清四种命题的定义及其关系,注意“且” “或”的
否定为“或” “且”。
解:逆命题:若m+n≤0,则m≤0或n≤0。
否命题:若m>0且n>0, 则m+n>0.
逆否命题:若m+n>0, 则m>0且n>0.
(真)
(真)
(假)
小结:在判断四种命题的真假时,只需判断两种命题的真假。因为逆命题与否命题真假等价,逆否命题与原命题真假等价。
巩固练习:P8练习
例3:证明x2+y2=0,则x=y=0.
小结: 1、本节内容: (1)四种命题的关系
(2)四种命题的真假关系
(3) 一种思想
