苏科版七年级数学上册 6.3 余角、补角、对顶角(共17张PPT)
文档属性
| 名称 | 苏科版七年级数学上册 6.3 余角、补角、对顶角(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 609.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 07:34:49 | ||
图片预览





文档简介
(共17张PPT)
6.3余角、补角、对顶角(2)
七年级(上册)
初中数学
教学目标:
1.掌握对顶角定义
2.熟练掌握对顶角性质及其应用
3.会运用互为余角、互为补角、对顶角的性质来解决问题.
A
B
O
B
A
∠AOB 与∠AOB叫做对顶角。
∠AOB与∠AOB也是对顶角。
对顶角有何特征?
(1)有公共的顶点;
(2)其中一个角的两边是另一个角的反向延长线。
定义:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
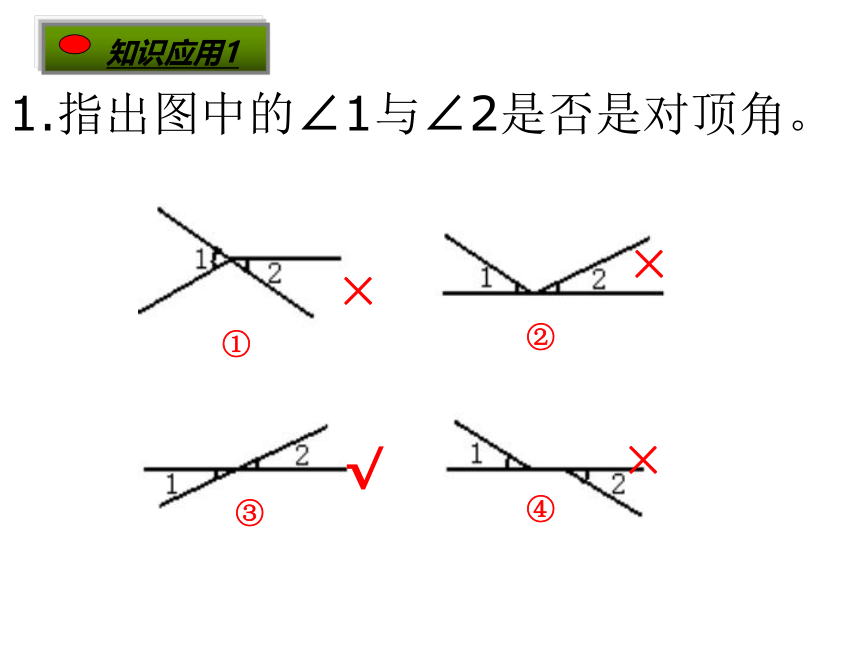
知识应用1
1.指出图中的∠1与∠2是否是对顶角。
①
②
③
④
√
×
×
×
成果展示:
1、下列各图中,∠l和∠2是对顶角吗?为什么?
2、如图,图中共有几对对顶角?
F
G
A
B
C
D
E
H
知识应用1
2.作出∠AOC的对顶角。
A
C
O
D
B
∠AOC和∠BOD有怎样的大小关系?为什么?
对顶角相等
E
如果OE平分∠AOC, ∠AOE=250,你能求出图中哪些角的度数?
例题学习
如图,AB、CD相交于点O,∠DOE=90,∠AOC=72,求∠BOE的度数。
0
0
A
B
C
D
E
O
2.如图,直线AB、CD、EF相交于点O,∠COE=20,∠BOF=25,求∠AOD的度数。
0
0
拓 展 练 习
1.书第161页练一练1、2、3题。
0
E
A
B
F
D
C
O
A
B
C
1、要测量两堵墙所成的角AOB的度数,但人不能进入围墙,如何测量
练一练
如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数.你能说出所量角是多少度吗?你的根据是什么?
答:40°
方法一:可利用对顶角相等得出。
方法二:可利用补角得出。
拓 展 练 习
3.如图,直线AB、CD相交于点O,OC是∠AOE的平分线,∠AOE=920,
求∠3、∠4的度数。
A
C
E
B
1
0
D
2
4
3
拓 展 练 习
4.(1)两条直线交于一点,有 对不同的对顶角;
(2)三条直线交于一点,有 对不同的对顶角;
(3)四条直线交于一点,有 对不同的对顶角;
(4)n 条直线交于一点,有 对不同的对顶角。
a3
a4
an
2
6
12
n(n-1)
a1
a2
知识就像一艘船
让它载着你
驶向你理想的彼岸
今天我们学到了什么 你能说出来吗
作业布置
1.课本164页6、8、9
2.课外作业《补充习题》、《课课练》对应内容
6.3余角、补角、对顶角(2)
七年级(上册)
初中数学
教学目标:
1.掌握对顶角定义
2.熟练掌握对顶角性质及其应用
3.会运用互为余角、互为补角、对顶角的性质来解决问题.
A
B
O
B
A
∠AOB 与∠AOB叫做对顶角。
∠AOB与∠AOB也是对顶角。
对顶角有何特征?
(1)有公共的顶点;
(2)其中一个角的两边是另一个角的反向延长线。
定义:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
知识应用1
1.指出图中的∠1与∠2是否是对顶角。
①
②
③
④
√
×
×
×
成果展示:
1、下列各图中,∠l和∠2是对顶角吗?为什么?
2、如图,图中共有几对对顶角?
F
G
A
B
C
D
E
H
知识应用1
2.作出∠AOC的对顶角。
A
C
O
D
B
∠AOC和∠BOD有怎样的大小关系?为什么?
对顶角相等
E
如果OE平分∠AOC, ∠AOE=250,你能求出图中哪些角的度数?
例题学习
如图,AB、CD相交于点O,∠DOE=90,∠AOC=72,求∠BOE的度数。
0
0
A
B
C
D
E
O
2.如图,直线AB、CD、EF相交于点O,∠COE=20,∠BOF=25,求∠AOD的度数。
0
0
拓 展 练 习
1.书第161页练一练1、2、3题。
0
E
A
B
F
D
C
O
A
B
C
1、要测量两堵墙所成的角AOB的度数,但人不能进入围墙,如何测量
练一练
如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数.你能说出所量角是多少度吗?你的根据是什么?
答:40°
方法一:可利用对顶角相等得出。
方法二:可利用补角得出。
拓 展 练 习
3.如图,直线AB、CD相交于点O,OC是∠AOE的平分线,∠AOE=920,
求∠3、∠4的度数。
A
C
E
B
1
0
D
2
4
3
拓 展 练 习
4.(1)两条直线交于一点,有 对不同的对顶角;
(2)三条直线交于一点,有 对不同的对顶角;
(3)四条直线交于一点,有 对不同的对顶角;
(4)n 条直线交于一点,有 对不同的对顶角。
a3
a4
an
2
6
12
n(n-1)
a1
a2
知识就像一艘船
让它载着你
驶向你理想的彼岸
今天我们学到了什么 你能说出来吗
作业布置
1.课本164页6、8、9
2.课外作业《补充习题》、《课课练》对应内容
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
