苏科版八年级数学上册 1.2 全等三角形(共24张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 1.2 全等三角形(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 07:53:16 | ||
图片预览





文档简介
(共24张PPT)
八年级 上册
1.2全等三角形
学习目标:
1.理解全等形的概念,并能识别图形
的全等.
2.理解全等三角形及其有关概念.
3.掌握全等三角形的性质,并能进行
简单的推理和计算.
学习重点、难点:
全等三角形的相关概念和性质.
学习说明
观察这些图片,你能看出形状、大小完全一样的几何图形吗?
生活中的全等形
你能再举出生活中的一些类似例子吗?
生活中的全等形
请同学们把一块三角尺按在纸板上,画下图形后,比较观察这两个三角形有何关系?从同一张底片冲洗出来的两张尺寸相同的照片上的图形,放在一起也能够完全重合吗?
全等形的定义:能够完全重合的两
个图形叫做全等形.
全等三角形的定义:能够完全重合
的两个三角形叫做全等三角形.
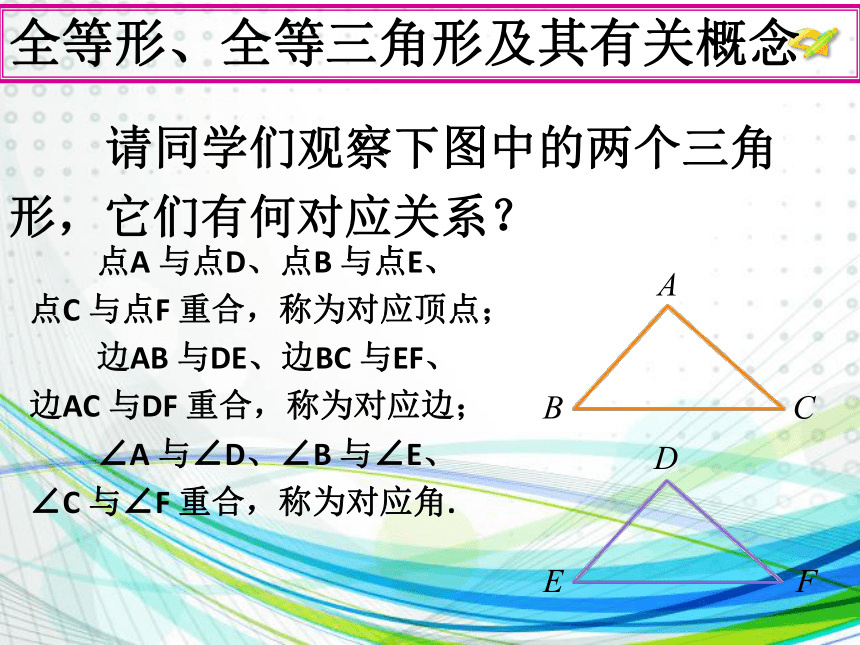
全等形、全等三角形及其有关概念
点A 与点D、点B 与点E、
点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、
边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、
∠C 与∠F 重合,称为对应角.
全等形、全等三角形及其有关概念
请同学们观察下图中的两个三角
形,它们有何对应关系?
A
B
C
D
E
F
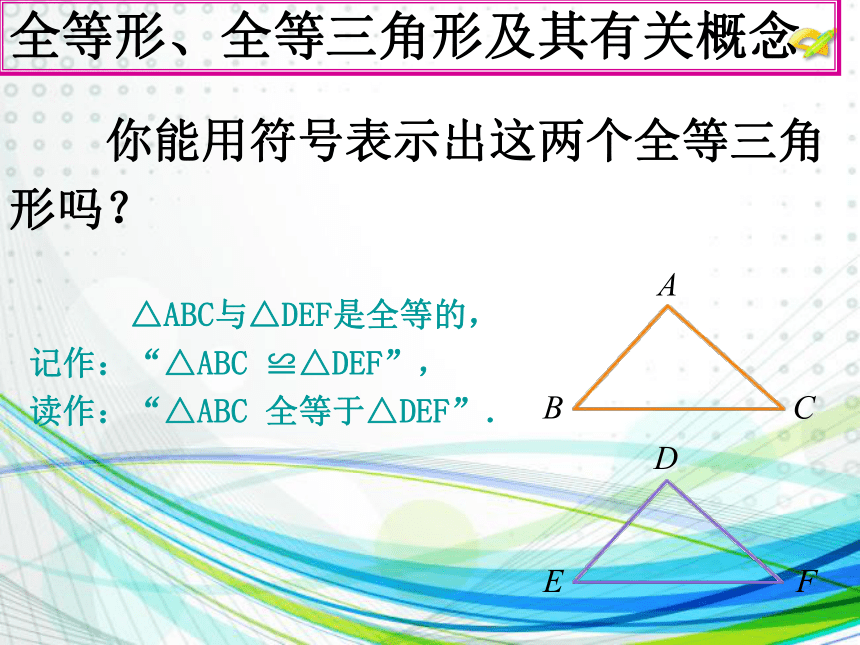
△ABC与△DEF是全等的,
记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”.
全等形、全等三角形及其有关概念
你能用符号表示出这两个全等三角
形吗?
A
B
C
D
E
F
图(1)中,△ABC ≌△DEF;
图(2)中,△ABC ≌△DBC;
图(3)中,△ABC ≌△DEC.
全等形、全等三角形及其有关概念
请同学们拿出准备的素材,按照教材第10页图1-4进行平移、翻折、旋转,变换前后的两个三角形还全等吗?
你能说出它们的对应顶点、对应边和对应
角吗?
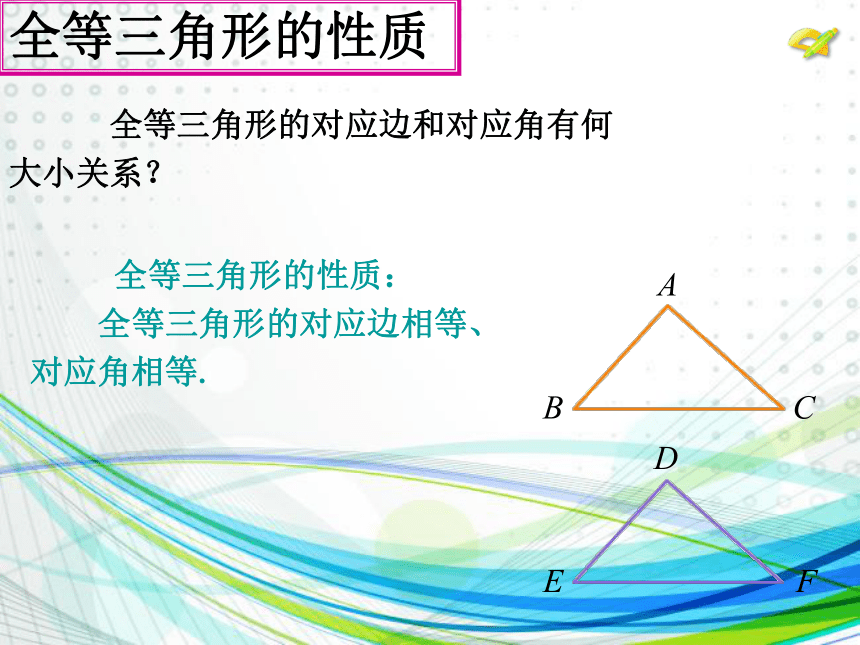
全等三角形的性质:
全等三角形的对应边相等、
对应角相等.
全等三角形的性质
全等三角形的对应边和对应角有何
大小关系?
A
B
C
D
E
F
用几何语言表述:
∵ △ABC ≌△DEF,
∴ AB =DE,BC =EF,AC =DF
(全等三角形的对应边相等),
∠A =∠D,∠B =∠E,∠C =∠F
(全等三角形的对应角相等).
全等三角形的性质
全等三角形的对应边和对应角有何
大小关系?
A
B
C
D
E
F
已知:如图,△ABC ≌△DEF.
(1)若DF =10 cm,则AC 的长为 ;
(2)若∠A =100°,则∠D 的度数为 ;
10 cm
100°
全等三角形的性质的运用
A
B
C
D
E
F
解:∵∠A =100°,∠B =30°,
∠A+∠B +∠C =180°
∴ ∠C =50°.
∵△DEF ≌△ABC ,
∴∠F =∠C(全等三角形的对应角相等).
∴∠F =50°
全等三角形的性质的运用
已知:如图,△ABC ≌△DEF.
(3)若∠A =100°,∠B =30°,求∠F 的度数.
A
B
C
D
E
F
D
课堂练习
练习1如图,△OCA ≌△OBD,点C 和点B,点A与点D是对应点,则下列结论错误的是( ).
A.∠COA =∠BOD;B.∠A =∠D;
C.CA =BD; D.OB =OA.
C
B
O
A
D
练习2△ABN ≌△ACM, ∠ABN 和∠ACM 是对应角,AB 和AC 是对应边.则下列结论错误的是( ).
A.∠AMC =∠ANB;B.∠BAN =∠CAM;
C.BM =MN; D.AM =AN.
C
课堂练习
A
B
C
M
N
练习3如图,△ABC ≌△CDA,AB 与CD,BC 与DA 是对应边,则下列结论错误的是( ).
A.∠BAC=∠DCA; B.AB//DC;
C.∠BCA=∠DCA;D.BC//DA.
C
A
B
C
D
课堂练习
练习4如图,△EFG ≌△NMH,∠F 和∠M 是对应角.
(1)FG 与MH 平行吗?为什么?
(2)判断线段EH 与NG 的大小关系,并说明理由.
(1)平行;
(2)相等.
H
E
N
G
F
M
课堂练习
A
B
C
D
∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,∠ABC=∠ABD,∠C= ∠D.
规律一:有公共边的,公共边是对应边
先写出全等式,再指出它们的对应边和对应角
探究交流
A
C
D
B
∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.
规律二:有对顶角的,对顶角是对应角
o
先写出全等式,再指出它们的对应边和对应角
探究交流
A
B
C
D
E
∵△ABC≌△ADE
∴AB=AD,AC=AE,BC=DE
∴∠A=∠A,∠B=∠D,∠ACB= ∠AED.
规律三:有公共角的,公共角是对应角
先写出全等式,再指出它们的对应边和对应角
探究交流
先写出全等式,再指出它们的对应边和对应角AC和EF为最长边,DE和AB为最短边
∵△ABC≌△FDE
∴AB=FD,AC=FE,BC=DE
∴∠A=∠F,∠B=∠D,
∠ACB=∠FED.
规律五:一对最大的角是对应角
一对最小的角是对应角
A
B
C
F
D
E
规律四:一对最长的边是对应边
一对最短的边是对应边
探究交流
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,对应边所
对的角是对应角.
5.在两个全等三角形中最长边对最长
边,最短边对最短边,最大角对最大
角,最小角对最小角。
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角。
规律
(1)本节课学习了哪些内容?
(2)结合本节课的学习,谈谈如何寻
找全等三角形的对应边、对应角?
(3)结合本节课的学习,谈谈经过平
移、翻折、旋转变换前后的两个图
形有何关系?
归纳小结
教科书12页习题1.2第1、2、3题.
布置作业
八年级 上册
1.2全等三角形
学习目标:
1.理解全等形的概念,并能识别图形
的全等.
2.理解全等三角形及其有关概念.
3.掌握全等三角形的性质,并能进行
简单的推理和计算.
学习重点、难点:
全等三角形的相关概念和性质.
学习说明
观察这些图片,你能看出形状、大小完全一样的几何图形吗?
生活中的全等形
你能再举出生活中的一些类似例子吗?
生活中的全等形
请同学们把一块三角尺按在纸板上,画下图形后,比较观察这两个三角形有何关系?从同一张底片冲洗出来的两张尺寸相同的照片上的图形,放在一起也能够完全重合吗?
全等形的定义:能够完全重合的两
个图形叫做全等形.
全等三角形的定义:能够完全重合
的两个三角形叫做全等三角形.
全等形、全等三角形及其有关概念
点A 与点D、点B 与点E、
点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、
边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、
∠C 与∠F 重合,称为对应角.
全等形、全等三角形及其有关概念
请同学们观察下图中的两个三角
形,它们有何对应关系?
A
B
C
D
E
F
△ABC与△DEF是全等的,
记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”.
全等形、全等三角形及其有关概念
你能用符号表示出这两个全等三角
形吗?
A
B
C
D
E
F
图(1)中,△ABC ≌△DEF;
图(2)中,△ABC ≌△DBC;
图(3)中,△ABC ≌△DEC.
全等形、全等三角形及其有关概念
请同学们拿出准备的素材,按照教材第10页图1-4进行平移、翻折、旋转,变换前后的两个三角形还全等吗?
你能说出它们的对应顶点、对应边和对应
角吗?
全等三角形的性质:
全等三角形的对应边相等、
对应角相等.
全等三角形的性质
全等三角形的对应边和对应角有何
大小关系?
A
B
C
D
E
F
用几何语言表述:
∵ △ABC ≌△DEF,
∴ AB =DE,BC =EF,AC =DF
(全等三角形的对应边相等),
∠A =∠D,∠B =∠E,∠C =∠F
(全等三角形的对应角相等).
全等三角形的性质
全等三角形的对应边和对应角有何
大小关系?
A
B
C
D
E
F
已知:如图,△ABC ≌△DEF.
(1)若DF =10 cm,则AC 的长为 ;
(2)若∠A =100°,则∠D 的度数为 ;
10 cm
100°
全等三角形的性质的运用
A
B
C
D
E
F
解:∵∠A =100°,∠B =30°,
∠A+∠B +∠C =180°
∴ ∠C =50°.
∵△DEF ≌△ABC ,
∴∠F =∠C(全等三角形的对应角相等).
∴∠F =50°
全等三角形的性质的运用
已知:如图,△ABC ≌△DEF.
(3)若∠A =100°,∠B =30°,求∠F 的度数.
A
B
C
D
E
F
D
课堂练习
练习1如图,△OCA ≌△OBD,点C 和点B,点A与点D是对应点,则下列结论错误的是( ).
A.∠COA =∠BOD;B.∠A =∠D;
C.CA =BD; D.OB =OA.
C
B
O
A
D
练习2△ABN ≌△ACM, ∠ABN 和∠ACM 是对应角,AB 和AC 是对应边.则下列结论错误的是( ).
A.∠AMC =∠ANB;B.∠BAN =∠CAM;
C.BM =MN; D.AM =AN.
C
课堂练习
A
B
C
M
N
练习3如图,△ABC ≌△CDA,AB 与CD,BC 与DA 是对应边,则下列结论错误的是( ).
A.∠BAC=∠DCA; B.AB//DC;
C.∠BCA=∠DCA;D.BC//DA.
C
A
B
C
D
课堂练习
练习4如图,△EFG ≌△NMH,∠F 和∠M 是对应角.
(1)FG 与MH 平行吗?为什么?
(2)判断线段EH 与NG 的大小关系,并说明理由.
(1)平行;
(2)相等.
H
E
N
G
F
M
课堂练习
A
B
C
D
∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,∠ABC=∠ABD,∠C= ∠D.
规律一:有公共边的,公共边是对应边
先写出全等式,再指出它们的对应边和对应角
探究交流
A
C
D
B
∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.
规律二:有对顶角的,对顶角是对应角
o
先写出全等式,再指出它们的对应边和对应角
探究交流
A
B
C
D
E
∵△ABC≌△ADE
∴AB=AD,AC=AE,BC=DE
∴∠A=∠A,∠B=∠D,∠ACB= ∠AED.
规律三:有公共角的,公共角是对应角
先写出全等式,再指出它们的对应边和对应角
探究交流
先写出全等式,再指出它们的对应边和对应角AC和EF为最长边,DE和AB为最短边
∵△ABC≌△FDE
∴AB=FD,AC=FE,BC=DE
∴∠A=∠F,∠B=∠D,
∠ACB=∠FED.
规律五:一对最大的角是对应角
一对最小的角是对应角
A
B
C
F
D
E
规律四:一对最长的边是对应边
一对最短的边是对应边
探究交流
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,对应边所
对的角是对应角.
5.在两个全等三角形中最长边对最长
边,最短边对最短边,最大角对最大
角,最小角对最小角。
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角。
规律
(1)本节课学习了哪些内容?
(2)结合本节课的学习,谈谈如何寻
找全等三角形的对应边、对应角?
(3)结合本节课的学习,谈谈经过平
移、翻折、旋转变换前后的两个图
形有何关系?
归纳小结
教科书12页习题1.2第1、2、3题.
布置作业
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
