苏科版八年级数学上册 3.3 勾股定理的简单应用(共21张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 3.3 勾股定理的简单应用(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 08:03:32 | ||
图片预览




文档简介
(共21张PPT)
义务教育课程标准实验教科书
人教版《数学》八年级下册
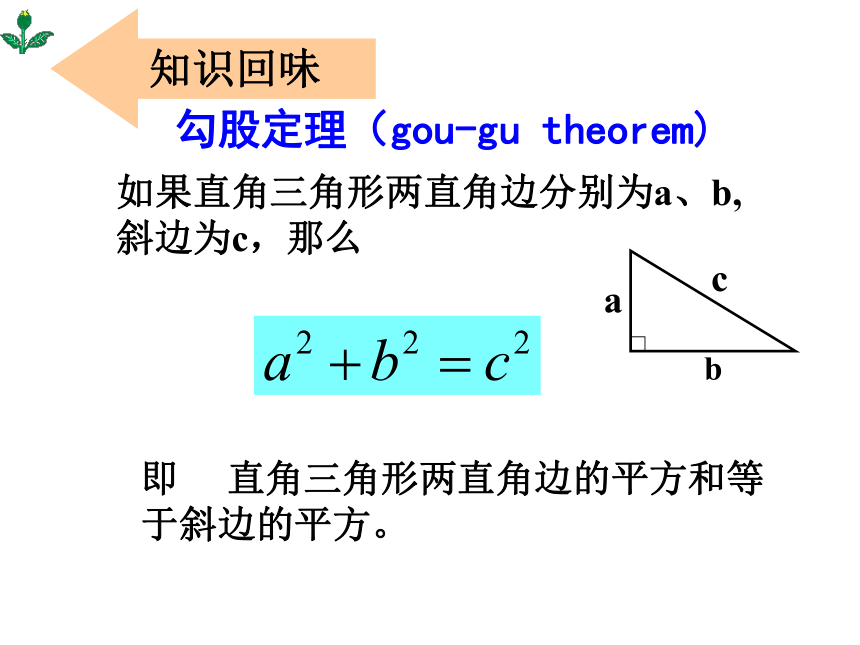
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
知识回味
请同学们完成下面的练习
(1)、在直角 三角形 ABC中,两条直角边a,b分别等于6和8,则斜边c等于( )。
(2)、直角三角形一直角边为9cm,斜边为15cm,则这个直角三角形的面积为( )cm2 。
(3)、一个等腰三角形的腰长为20cm,底边长为24cm,则底边上的高为( )cm,面积为( )cm2 。
10
课前热身
54
16
192
(4)、判断题.
▲ ABC的两边AB=5,AC=12,则BC=13 ( )
▲ ABC的a=6,b=8,则c=10 ( )
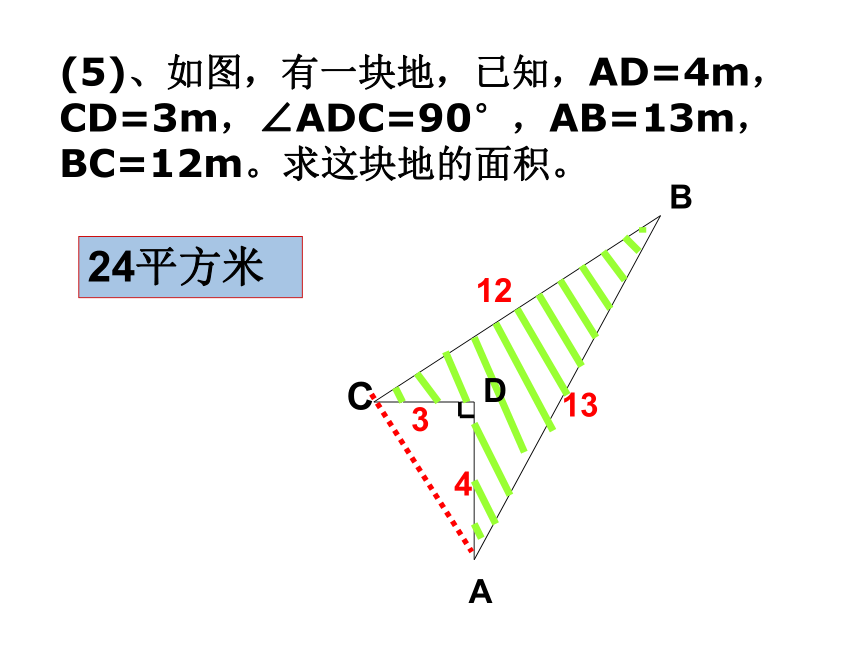
(5)、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
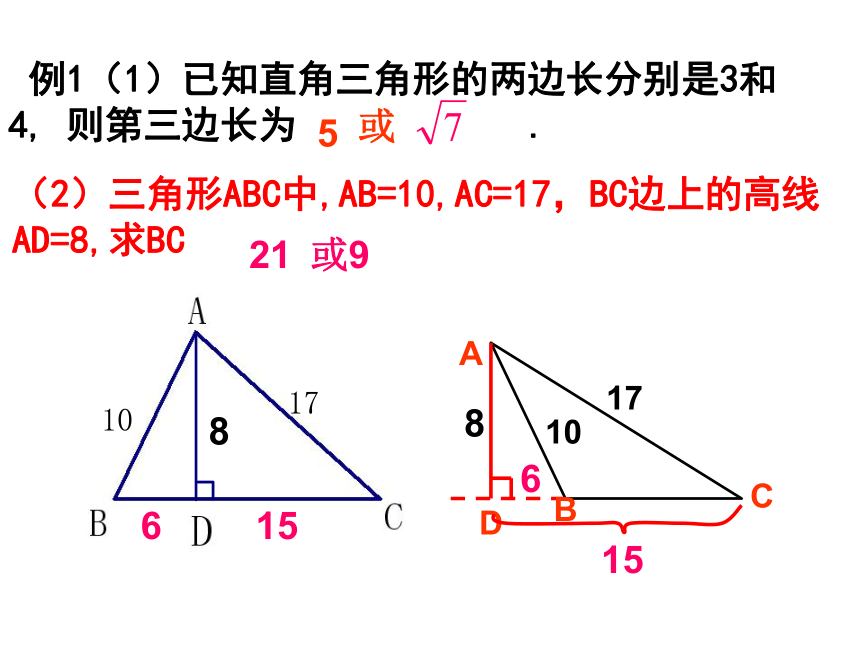
(2)三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
A
B
C
例1(1)已知直角三角形的两边长分别是3和4, 则第三边长为 .
5
或
17
10
8
D
8
6
15
15
6
21
或9
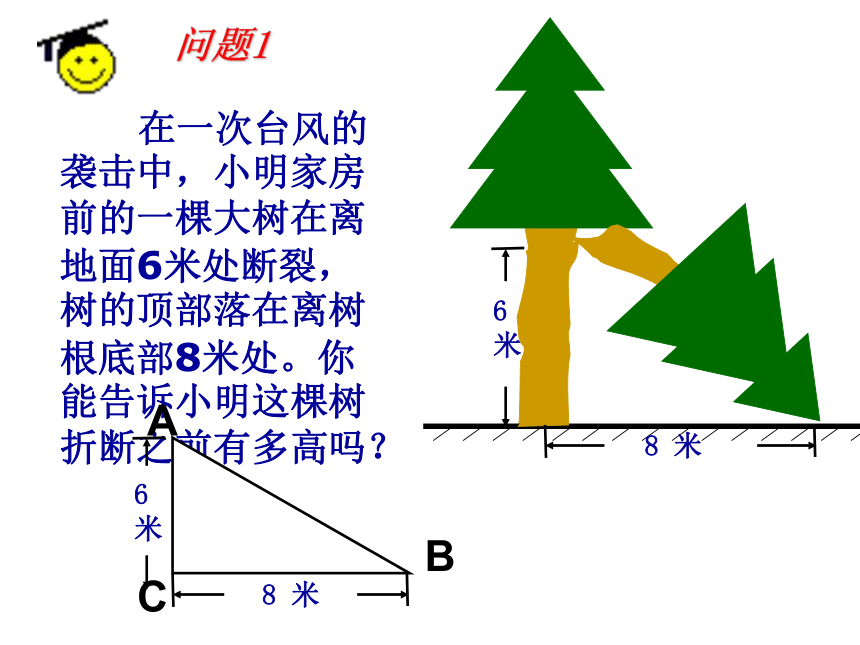
在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
问题1
8 米
6米
A
C
B
6米
8 米
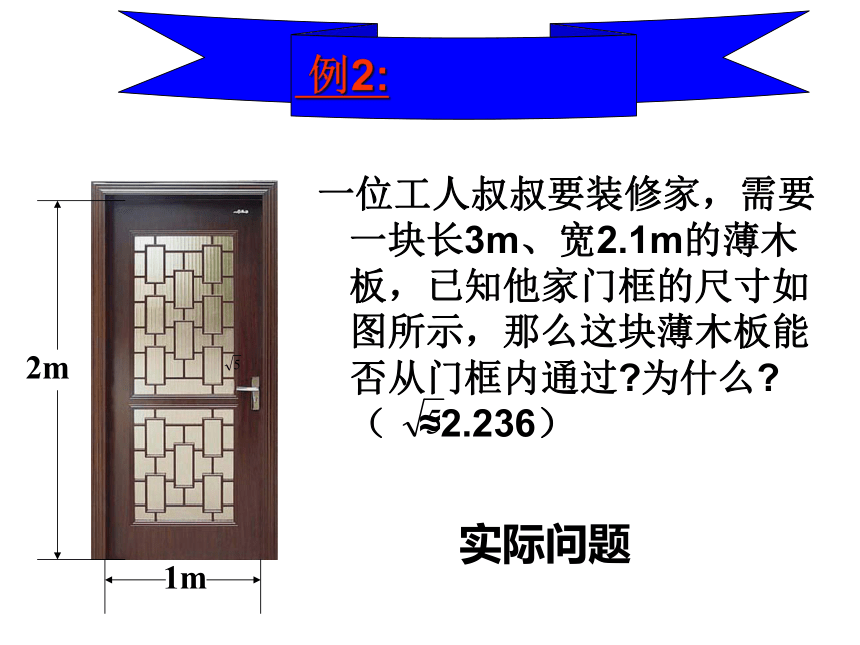
一位工人叔叔要装修家,需要一块长3m、宽2.1m的薄木板,已知他家门框的尺寸如图所示,那么这块薄木板能否从门框内通过 为什么 ( ≈2.236)
1m
2m
例2:
实际问题
思考
1m
2m
A
D
C
B
2.1米
3米
1m
2m
解答
A
D
C
B
解:连结AC,在Rt△ABC中AB=2m, BC=1m ∠B=90°,根据勾股定理:
>2.1m
∴薄木板能从门框内通过。
1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
解设AC的长为 X 米,
则AB=(x+1)米
过关斩将
在RtΔABC中,
方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
例:3、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
例4:折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求: (1) CF (2) EC
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
1、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
解:连结BE
由已知可知:DE是AB的中垂线,∴AE=BE
在Rt△ABC 中,根据勾股定理:
设AE=xcm,则EC=(10-x)cm
BE2=BC2+EC2
x2=62+ (10-x)2
解得x=6.8
∴EC=10-6.8=3.2cm
超越自我
2、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
解:由已知AF=FC
设AF=x,则FB=9-x
在R t △ABC中,根据勾股定理FC2=FB2+BC2
则有x2=(9-x)2+32
解得x=5
同理可得DE=4
∴GF=1
∴以EF为边的正方形的面积=EG2+GF2=32+12=10
1、通过这节课的学习活动你有哪些收获?
2、对这节课的学习,你还有什么想法吗?
作业:填空题 1.在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 2.在 ABC中, C=90°,若AC=6,CB=8,则 ABC面积为_____,斜边为上的高为______.
6
8
41
24
4.8
作业二:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,如图水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
解:设AD=x,则AB=x,AC=x-1
在RtΔABC中,
选做题:如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B、C 两个村庄,现要在 B、C两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园 请通过计算说明.
A
B
C
400
1000
60°
30°
D
义务教育课程标准实验教科书
人教版《数学》八年级下册
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
知识回味
请同学们完成下面的练习
(1)、在直角 三角形 ABC中,两条直角边a,b分别等于6和8,则斜边c等于( )。
(2)、直角三角形一直角边为9cm,斜边为15cm,则这个直角三角形的面积为( )cm2 。
(3)、一个等腰三角形的腰长为20cm,底边长为24cm,则底边上的高为( )cm,面积为( )cm2 。
10
课前热身
54
16
192
(4)、判断题.
▲ ABC的两边AB=5,AC=12,则BC=13 ( )
▲ ABC的a=6,b=8,则c=10 ( )
(5)、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
(2)三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
A
B
C
例1(1)已知直角三角形的两边长分别是3和4, 则第三边长为 .
5
或
17
10
8
D
8
6
15
15
6
21
或9
在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
问题1
8 米
6米
A
C
B
6米
8 米
一位工人叔叔要装修家,需要一块长3m、宽2.1m的薄木板,已知他家门框的尺寸如图所示,那么这块薄木板能否从门框内通过 为什么 ( ≈2.236)
1m
2m
例2:
实际问题
思考
1m
2m
A
D
C
B
2.1米
3米
1m
2m
解答
A
D
C
B
解:连结AC,在Rt△ABC中AB=2m, BC=1m ∠B=90°,根据勾股定理:
>2.1m
∴薄木板能从门框内通过。
1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
解设AC的长为 X 米,
则AB=(x+1)米
过关斩将
在RtΔABC中,
方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
例:3、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
例4:折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求: (1) CF (2) EC
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
1、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
解:连结BE
由已知可知:DE是AB的中垂线,∴AE=BE
在Rt△ABC 中,根据勾股定理:
设AE=xcm,则EC=(10-x)cm
BE2=BC2+EC2
x2=62+ (10-x)2
解得x=6.8
∴EC=10-6.8=3.2cm
超越自我
2、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
解:由已知AF=FC
设AF=x,则FB=9-x
在R t △ABC中,根据勾股定理FC2=FB2+BC2
则有x2=(9-x)2+32
解得x=5
同理可得DE=4
∴GF=1
∴以EF为边的正方形的面积=EG2+GF2=32+12=10
1、通过这节课的学习活动你有哪些收获?
2、对这节课的学习,你还有什么想法吗?
作业:填空题 1.在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 2.在 ABC中, C=90°,若AC=6,CB=8,则 ABC面积为_____,斜边为上的高为______.
6
8
41
24
4.8
作业二:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,如图水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
解:设AD=x,则AB=x,AC=x-1
在RtΔABC中,
选做题:如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B、C 两个村庄,现要在 B、C两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园 请通过计算说明.
A
B
C
400
1000
60°
30°
D
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
