苏科版八年级数学上册 5.2 平面直角坐标系(共26张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 5.2 平面直角坐标系(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 08:31:43 | ||
图片预览





文档简介
(共26张PPT)
位置的确定
5.2 平面直角坐标系(1)
八年级(上册)
初中数学
数缺形时少直观
形离数时难入微
5.2 平面直角坐标系(1)
怎样确定一条直线上的点的位置?
P
数轴上的点与实数一一对应
怎样表示平面内 的点的位置?
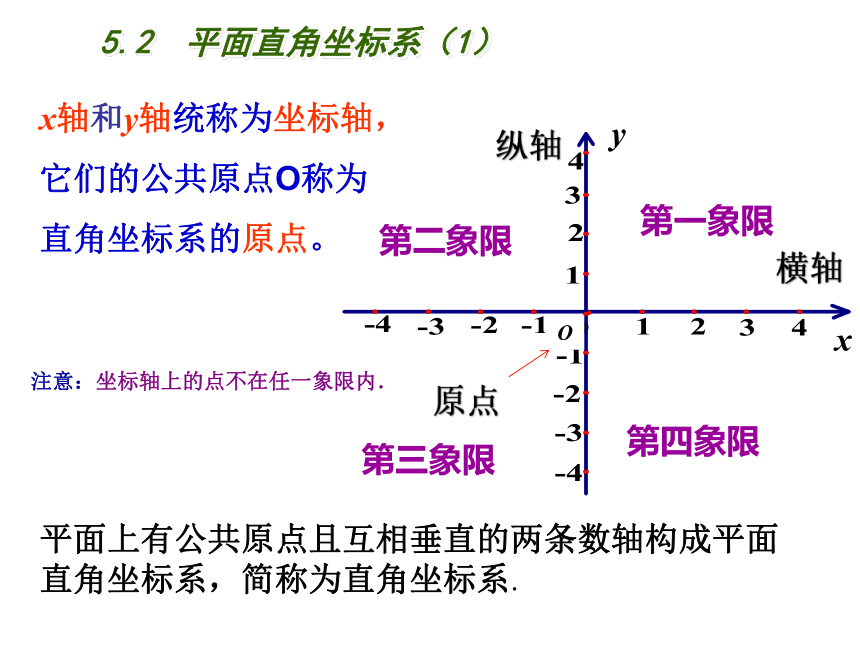
x轴和y轴统称为坐标轴,
它们的公共原点O称为
直角坐标系的原点。
第二象限
5.2 平面直角坐标系(1)
x
y
x
y
O
x
y
平面上有公共原点且互相垂直的两条数轴构成平面直角坐标系,简称为直角坐标系.
横轴
纵轴
原点
第一象限
第三象限
第四象限
注意:坐标轴上的点不在任一象限内.
x
y
o
-1
1
-1
1
m
n
P
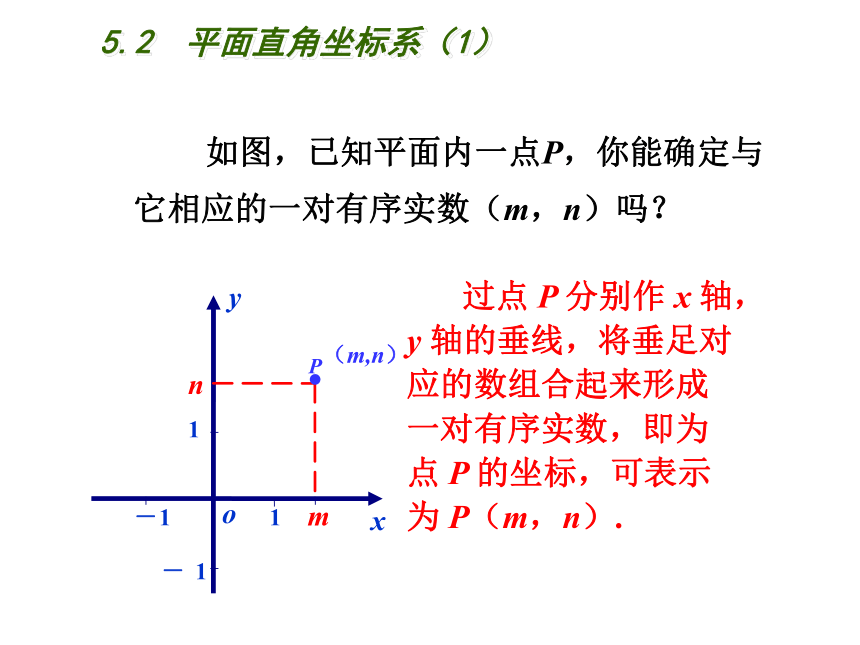
如图,已知平面内一点P,你能确定与它相应的一对有序实数(m,n)吗?
(m,n)
过点 P 分别作 x 轴,y 轴的垂线,将垂足对应的数组合起来形成一对有序实数,即为点 P 的坐标,可表示为 P(m,n).
5.2 平面直角坐标系(1)
对于平面内任意一点P,过点P分别向X轴
、Y轴作垂线,垂足在X轴、Y轴上对应的
数a、b分别叫做点P的_________和
________有序实数对是_________,就叫做
p的________。
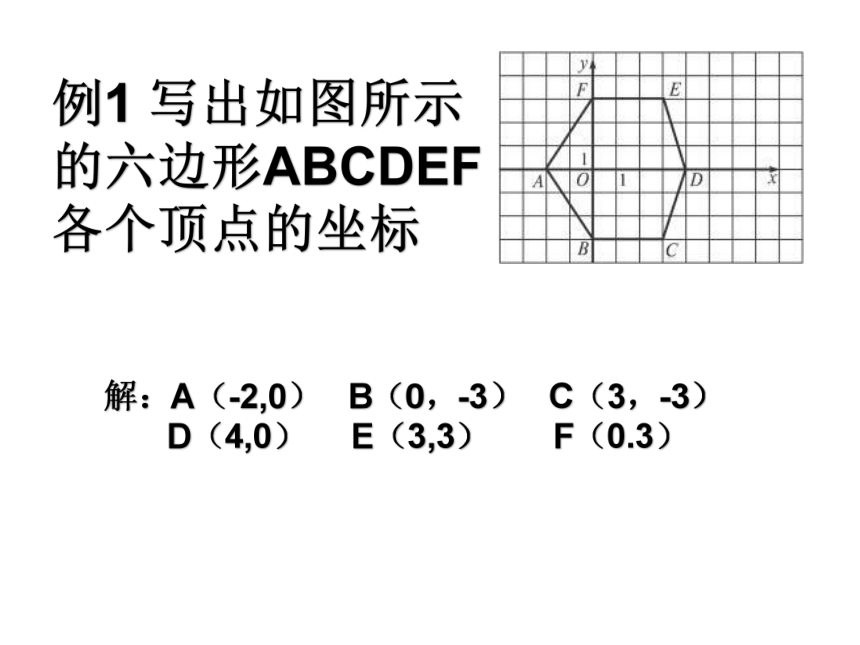
例1 写出如图所示
的六边形ABCDEF
各个顶点的坐标
解:A(-2,0) B(0,-3) C(3,-3)
D(4,0) E(3,3) F(0.3)
y
o
-1
1
-1
1
a
b
P
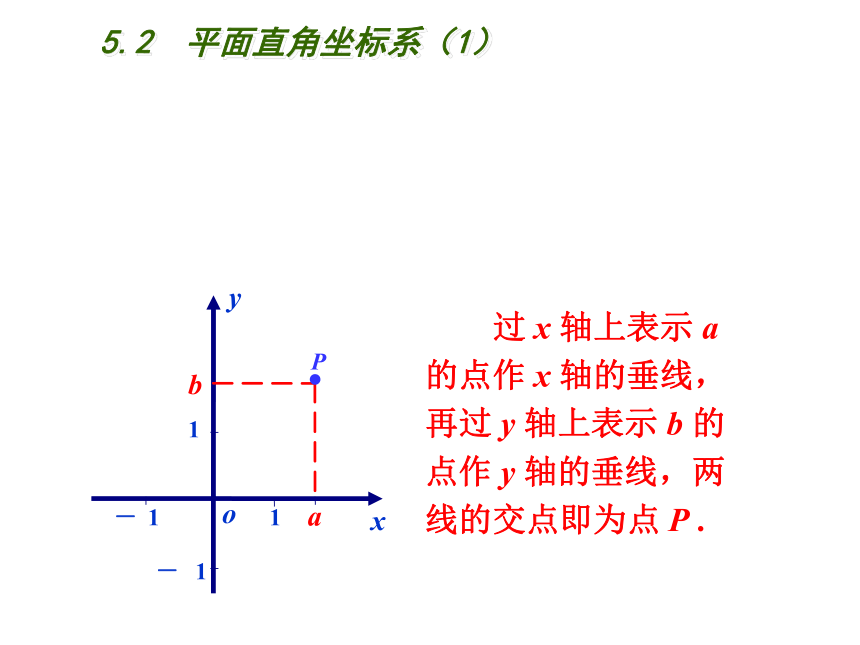
过 x 轴上表示 a的点作 x 轴的垂线,再过 y 轴上表示 b 的点作 y 轴的垂线,两线的交点即为点 P .
x
5.2 平面直角坐标系(1)
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
(4,1)
B
(-1,4)
C
D
例1 在直角坐标系中,描出下列各点的位置:
A(4,1),B(-1,4),C(-4,-2),D(3,-2),
E(0,1 ),F( -4,0 ) .
x
(-4,-2)
E
(0,1)
F
(-4,0)
(3,-2)
5.2 平面直角坐标系(1)
1.在平面直角坐标系中,一对有序实数可以确 定一个点的位置;反之,任意一点的位置都可以用一对有序实数来表示.这样的有序实数对叫做点的坐标.
2.点的坐标通常与表示该点的大写字母写在一起,如 P(a,b),Q(m,n).
5.2 平面直角坐标系(1)
北京西路
北京东路
中山北路
中山南路
小丽:“音乐喷泉在哪里?”小明:“中山北路西边50m,北京西路北边30m” 小丽能按小明的描述,找到音乐喷泉吗?
50 m
30 m
-10
10
10
-10
O
-50
30
(
)
,
5.2 平面直角坐标系(1)
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
例 2 写出图中点A、B、C 的坐标.
x
.
A
.
.
B
C
(-4,3)
(-3,-2)
(1 ,-3)
第一象限
第二象限
第四象限
第三象限
5.2 平面直角坐标系(1)
探究1 四个象限内的点的坐标的符号特征
探究2 坐标轴上的点的特征
探究3 平行于X轴或Y轴的直线上的点的特征
探究4 点到坐标轴的距离
探究1、各象限内的点的坐标有何特征?
(-3,3)
(3,2)
(2,3)
(-7,2)
(-5,-4)
(-7,-5)
(3,-5)
(5,-4)
(-,+)
(+,+)
(-,-)
(+,-)
-1
-2
-4
-3
-5
1
2
3
4
5
1
o
2
3
4
6
5
7
8
9
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
y
A
B
C
D
E
F
G
H
探究2、坐标轴上点有何特征?
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
(3,0)
A
(-4,0)
B
(0,0)
(0,5)
C
(0,-4)
D
在x轴上的点,纵坐标等于0;
在y轴上的点,横坐标等于0;
探究3 平行于X轴或Y轴的直线上的点的特征
-1
-2
-4
-3
-5
1
2
3
4
5
1
o
2
3
4
6
5
7
8
9
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
y
A( 3, 2 )
B( 0,-2 )
C(-3,-2)
D(-3, 0 )
E(-1.5,3.5)
F( 2, -3 )
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
练一练:
下列各点分别在坐标平面的什么位置上?
2.若点P(x,y)在
(1)第一象限,则x____0,y____0
(2)第二象限,则x____0,y____0
(3)第三象限,则x____0,y____0
(4)第四象限,则x____0,y____0
(5)x轴上,则x________,y_________
(6)y轴上,则x________,y_________
(7)原点上,则x________,y_________
>
>
>
>
<
<
<
<
任意值
任意值
=0
=0
=0
=0
一、判断:
1、对于坐标平面内的任一点,都有唯 一的一对有序实数与它对应.( )
2、在直角坐标系内,原点的坐标是0.( )
3、点A(a ,-b )在第二象限,则点B(-a,b)在第四象限. ( )
4、若点P的坐标为(a,b),且a·b=0,则点P一定在坐标原点. ( )
√
√
×
×
三、已知 P 点坐标为(2 a + 1,a-3)
( 1 ) 点 P 在 x 轴上,则 a= ;
( 2 ) 点 P 在 y 轴上,则 a= ;
四、若点 P(x,y)在第四象限,| x |=5,| y |=4,则 P 点的坐标为 .
3
(5,-4)
5.2 平面直角坐标系(1)
5.2 平面直角坐标系(1)
四、若点 P(x-2,x+3)在第一象限,则x的
取值范围是____________.
探索点的坐标的几何意义:
已知点A(a,b),过点A作x轴的垂线,垂足为B,过点A作y轴的垂线,垂足为C.
(1) 四边形OBAC是矩形吗?
(2) 线段AB的长度与点A的坐标有什么数量关系?
(3) 线段AC的长度与点A的坐标有什么数量关系?
5.2 平面直角坐标系(1)
今天我们学到了什么?
1.怎样建立坐标系?
3.坐标平面内的点与有序实数对之间的关系
一一对应
4.不同位置的点的坐标的特征
2.能在直角坐标系中,根据坐标找出点,
由点求出坐标
阅读与欣赏——笛卡儿的梦
笛卡儿(1596—1650年)法国著名的数学家,青年时期曾参加军队到荷兰。1619年的冬天,莱茵河畔乌儿小镇的军用帐篷中。入夜, 万簌俱静,笛卡儿彻夜不眠,沉迷在深思之中,他望着天空,想着怎么用几个数字来表示星星的位置呢?自己随军奔波,给家里去信怎么报告自己的位置呢?他完全进入数学的世界,继续进行着数与形的冥想……
他仿佛到了无人的旷野,他的排长站在他的面前说:“你不是想用数学来解释自然界吗?”排长说着抽出了两支箭,拿在手里搭成一个十字架,箭头一个向上,一个朝右。他将十字架举过头说:“你看,假如我们把天空的一部分看成是一个平面,这个天空就被分成四个部分。这两支箭能射向无限远,天上随便那颗星星,你只要向这两支箭上分别引垂线段,就会得到两个数字,这星的位置就一清二楚了。”笛卡儿还不清楚又问道“负数又该怎样表示呢?”排长笑道:“两支箭的十字交叉处定为零,向上向右为正数,向下向左不就是负数了吗?”笛卡儿高兴地扑了过去,却扑通一声跌入河中……正在大喊,却被人叫醒 ,天已大亮了。笛卡儿发疯似地拿出本子和铅笔,把梦中见到的全都画了出来。后人传说笛卡儿创立的直角坐标系就是这样从梦中得来的。
直角坐标系的创立,为用代数方法研究几何问题开辟了一条崭新的道路,引起了数学的深刻革命。为了纪念笛卡儿,直角坐标系也叫笛卡儿坐标系。
位置的确定
5.2 平面直角坐标系(1)
八年级(上册)
初中数学
数缺形时少直观
形离数时难入微
5.2 平面直角坐标系(1)
怎样确定一条直线上的点的位置?
P
数轴上的点与实数一一对应
怎样表示平面内 的点的位置?
x轴和y轴统称为坐标轴,
它们的公共原点O称为
直角坐标系的原点。
第二象限
5.2 平面直角坐标系(1)
x
y
x
y
O
x
y
平面上有公共原点且互相垂直的两条数轴构成平面直角坐标系,简称为直角坐标系.
横轴
纵轴
原点
第一象限
第三象限
第四象限
注意:坐标轴上的点不在任一象限内.
x
y
o
-1
1
-1
1
m
n
P
如图,已知平面内一点P,你能确定与它相应的一对有序实数(m,n)吗?
(m,n)
过点 P 分别作 x 轴,y 轴的垂线,将垂足对应的数组合起来形成一对有序实数,即为点 P 的坐标,可表示为 P(m,n).
5.2 平面直角坐标系(1)
对于平面内任意一点P,过点P分别向X轴
、Y轴作垂线,垂足在X轴、Y轴上对应的
数a、b分别叫做点P的_________和
________有序实数对是_________,就叫做
p的________。
例1 写出如图所示
的六边形ABCDEF
各个顶点的坐标
解:A(-2,0) B(0,-3) C(3,-3)
D(4,0) E(3,3) F(0.3)
y
o
-1
1
-1
1
a
b
P
过 x 轴上表示 a的点作 x 轴的垂线,再过 y 轴上表示 b 的点作 y 轴的垂线,两线的交点即为点 P .
x
5.2 平面直角坐标系(1)
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
(4,1)
B
(-1,4)
C
D
例1 在直角坐标系中,描出下列各点的位置:
A(4,1),B(-1,4),C(-4,-2),D(3,-2),
E(0,1 ),F( -4,0 ) .
x
(-4,-2)
E
(0,1)
F
(-4,0)
(3,-2)
5.2 平面直角坐标系(1)
1.在平面直角坐标系中,一对有序实数可以确 定一个点的位置;反之,任意一点的位置都可以用一对有序实数来表示.这样的有序实数对叫做点的坐标.
2.点的坐标通常与表示该点的大写字母写在一起,如 P(a,b),Q(m,n).
5.2 平面直角坐标系(1)
北京西路
北京东路
中山北路
中山南路
小丽:“音乐喷泉在哪里?”小明:“中山北路西边50m,北京西路北边30m” 小丽能按小明的描述,找到音乐喷泉吗?
50 m
30 m
-10
10
10
-10
O
-50
30
(
)
,
5.2 平面直角坐标系(1)
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
例 2 写出图中点A、B、C 的坐标.
x
.
A
.
.
B
C
(-4,3)
(-3,-2)
(1 ,-3)
第一象限
第二象限
第四象限
第三象限
5.2 平面直角坐标系(1)
探究1 四个象限内的点的坐标的符号特征
探究2 坐标轴上的点的特征
探究3 平行于X轴或Y轴的直线上的点的特征
探究4 点到坐标轴的距离
探究1、各象限内的点的坐标有何特征?
(-3,3)
(3,2)
(2,3)
(-7,2)
(-5,-4)
(-7,-5)
(3,-5)
(5,-4)
(-,+)
(+,+)
(-,-)
(+,-)
-1
-2
-4
-3
-5
1
2
3
4
5
1
o
2
3
4
6
5
7
8
9
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
y
A
B
C
D
E
F
G
H
探究2、坐标轴上点有何特征?
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
(3,0)
A
(-4,0)
B
(0,0)
(0,5)
C
(0,-4)
D
在x轴上的点,纵坐标等于0;
在y轴上的点,横坐标等于0;
探究3 平行于X轴或Y轴的直线上的点的特征
-1
-2
-4
-3
-5
1
2
3
4
5
1
o
2
3
4
6
5
7
8
9
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
y
A( 3, 2 )
B( 0,-2 )
C(-3,-2)
D(-3, 0 )
E(-1.5,3.5)
F( 2, -3 )
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
练一练:
下列各点分别在坐标平面的什么位置上?
2.若点P(x,y)在
(1)第一象限,则x____0,y____0
(2)第二象限,则x____0,y____0
(3)第三象限,则x____0,y____0
(4)第四象限,则x____0,y____0
(5)x轴上,则x________,y_________
(6)y轴上,则x________,y_________
(7)原点上,则x________,y_________
>
>
>
>
<
<
<
<
任意值
任意值
=0
=0
=0
=0
一、判断:
1、对于坐标平面内的任一点,都有唯 一的一对有序实数与它对应.( )
2、在直角坐标系内,原点的坐标是0.( )
3、点A(a ,-b )在第二象限,则点B(-a,b)在第四象限. ( )
4、若点P的坐标为(a,b),且a·b=0,则点P一定在坐标原点. ( )
√
√
×
×
三、已知 P 点坐标为(2 a + 1,a-3)
( 1 ) 点 P 在 x 轴上,则 a= ;
( 2 ) 点 P 在 y 轴上,则 a= ;
四、若点 P(x,y)在第四象限,| x |=5,| y |=4,则 P 点的坐标为 .
3
(5,-4)
5.2 平面直角坐标系(1)
5.2 平面直角坐标系(1)
四、若点 P(x-2,x+3)在第一象限,则x的
取值范围是____________.
探索点的坐标的几何意义:
已知点A(a,b),过点A作x轴的垂线,垂足为B,过点A作y轴的垂线,垂足为C.
(1) 四边形OBAC是矩形吗?
(2) 线段AB的长度与点A的坐标有什么数量关系?
(3) 线段AC的长度与点A的坐标有什么数量关系?
5.2 平面直角坐标系(1)
今天我们学到了什么?
1.怎样建立坐标系?
3.坐标平面内的点与有序实数对之间的关系
一一对应
4.不同位置的点的坐标的特征
2.能在直角坐标系中,根据坐标找出点,
由点求出坐标
阅读与欣赏——笛卡儿的梦
笛卡儿(1596—1650年)法国著名的数学家,青年时期曾参加军队到荷兰。1619年的冬天,莱茵河畔乌儿小镇的军用帐篷中。入夜, 万簌俱静,笛卡儿彻夜不眠,沉迷在深思之中,他望着天空,想着怎么用几个数字来表示星星的位置呢?自己随军奔波,给家里去信怎么报告自己的位置呢?他完全进入数学的世界,继续进行着数与形的冥想……
他仿佛到了无人的旷野,他的排长站在他的面前说:“你不是想用数学来解释自然界吗?”排长说着抽出了两支箭,拿在手里搭成一个十字架,箭头一个向上,一个朝右。他将十字架举过头说:“你看,假如我们把天空的一部分看成是一个平面,这个天空就被分成四个部分。这两支箭能射向无限远,天上随便那颗星星,你只要向这两支箭上分别引垂线段,就会得到两个数字,这星的位置就一清二楚了。”笛卡儿还不清楚又问道“负数又该怎样表示呢?”排长笑道:“两支箭的十字交叉处定为零,向上向右为正数,向下向左不就是负数了吗?”笛卡儿高兴地扑了过去,却扑通一声跌入河中……正在大喊,却被人叫醒 ,天已大亮了。笛卡儿发疯似地拿出本子和铅笔,把梦中见到的全都画了出来。后人传说笛卡儿创立的直角坐标系就是这样从梦中得来的。
直角坐标系的创立,为用代数方法研究几何问题开辟了一条崭新的道路,引起了数学的深刻革命。为了纪念笛卡儿,直角坐标系也叫笛卡儿坐标系。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
